数学八年级上人教新课标(新版)13.3等腰三角形课件(第三课时)
文档属性
| 名称 | 数学八年级上人教新课标(新版)13.3等腰三角形课件(第三课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 764.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-10 00:00:00 | ||
图片预览





文档简介
课件27张PPT。八年级 上册13.3 等腰三角形
(第3课时)课件说明本节课是在学生学习了轴对称和等腰三角形的性质
和判定的基础上,探索等边三角形的性质和判定方
法.
学习目标:
1.探索等边三角形的性质和判定.
2.能运用等边三角形的性质和判定进行计算和证
明.
学习重点:
探索等边三角形的性质与判定.课件说明 下列图片中有你熟悉的数学图形吗?你能说出此
图形的名称吗?
创设情境,导入新知三条边都相等的三角形是等边三角形. 创设情境,导入新知 问题 满足什么条件的三角形是等边三角形? 联系:等边三角形是特殊的等腰三角形;
区别:等边三角形有三条相等的边,而等腰三角形
只有两条.创设情境,导入新知 请分别画出一个等腰三角形和等边三角形,结合
你画的图形说出它们有什么区别和联系? 思考 将等腰三角形的性质用于等边三角形,你能
得到什么结论?
从边的角度:两腰相等;
从角的角度:等边对等角;
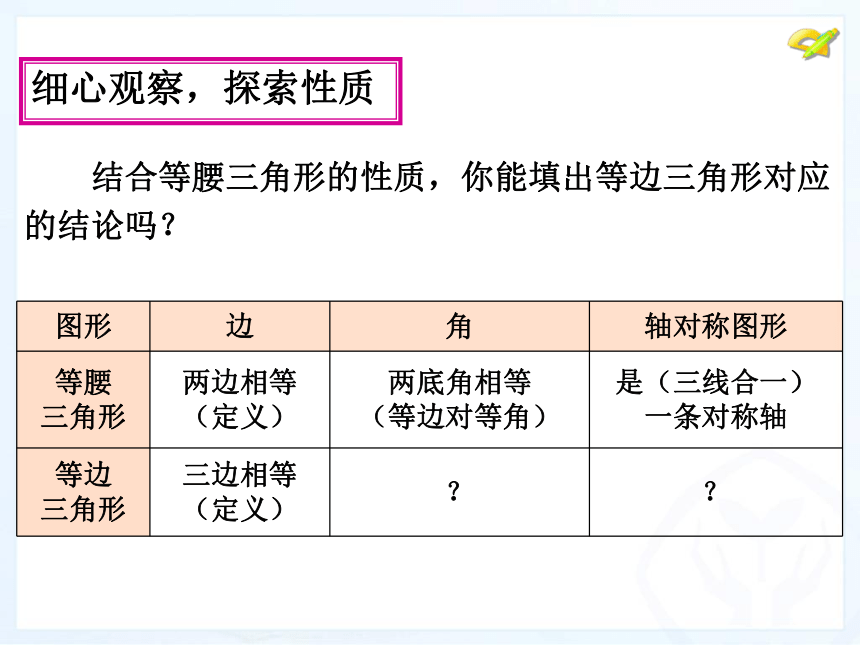
从对称性的角度:轴对称图形、三线合一.细心观察,探索性质 问题 等腰三角形有哪些特殊的性质呢? 细心观察,探索性质 结合等腰三角形的性质,你能填出等边三角形对应
的结论吗? 细心观察,探索性质 结合等腰三角形的性质,你能填出等边三角形对应
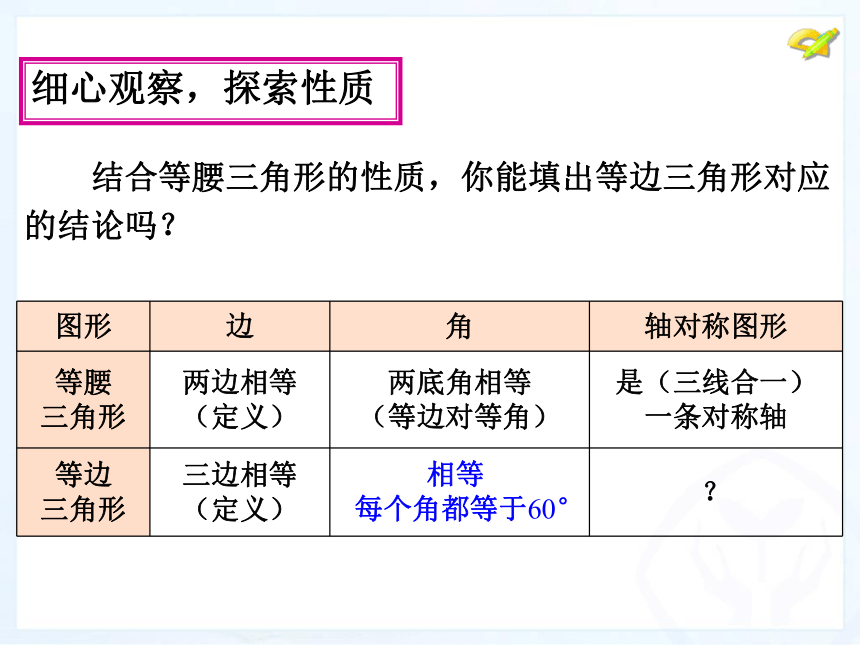
的结论吗? 相等
每个角都等于60° 相等
每个角都等于60°细心观察,探索性质 结合等腰三角形的性质,你能填出等边三角形对应
的结论吗? 是(三线合一)
三条对称轴 对“等边三角形的三个内角都相等,并且每一个角
都等于60°”这一结论进行证明.细心观察,探索性质
证明:∵ △ABC 是等边三角形,
∴ BC =AC,BC =AB.
∴ ∠A =∠B,∠A =∠C .
∴ ∠A =∠B =∠C .
∵ ∠A +∠B +∠C =180°,
∴ ∠A =60°.
∴ ∠A =∠B =∠C =60°.细心观察,探索性质 已知:△ABC 是等边三角形 求证:∠A =∠B =∠C
=60°. 符号语言:
∵ △ABC 是等边三角形,
∴ ∠A =∠B =∠C =60°.细心观察,探索性质 等边三角形的性质:
等边三角形的三个内角都相等,并且每一个角都等
于60°.细心观察,探索性质 思考 利用所学知识判断,等边三角形是轴对称图形吗?若是轴对称图形,请画出它的对称轴.
思考1 一个三角形的三个内角满足什么条件是等
边三角形? 三个角都相等的三角形或者一个角为60°的等腰三
角形. 思考2 一个等腰三角形满足什么条件是等边三角
形?细心观察,探索性质 问题 等边三角形除了用定义(即用边)来判定以
外,能否利用角来判定呢?细心观察,探索性质 请你将得到的这两个命题进行证明. 一般三角形 证明:∵ ∠A =∠B,∠B =∠C ,
∴ BC =AC, AC =AB.
∴ AB =BC =AC.
∴ △ABC 是等边三角形. 已知:在△ABC 中,∠A=∠B=∠C.求证:△ABC
是等边三角形.细心观察,探索性质细心观察,探索性质 已知:在△ABC 中,AC =BC且∠A =60°.求证:
△ABC是等边三角形.证明:略. 符号语言:
在△ABC 中,
∵ ∠A=∠B =∠C ,
∴ △ABC 是等边三角形.细心观察,探索性质 等边三角形的判定定理1:
三个角都相等的三角形是等边三角形. 细心观察,探索性质 等边三角形的判定定理2:
有一个角为60°的等腰三角形是等边三角形. 符号语言:
在△ABC 中,
∵ BC =AC,∠A =60°,
∴ △ABC 是等边三角形. 等边三角形的判定定理1:
三个角都相等的三角形是等边三角形.
等边三角形的判定定理2:
有一个角为60°的等腰三角形. 细心观察,概括归纳 判定等边三角形的方法:
从边的角度:等边三角形的定义;
从角的角度:等边三角形的两条判定定理. 证明: ∵ △ABC 是等边三角形,
∴ ∠A =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠ADE,∠C =∠AED.
∴ ∠A=∠ADE =∠AED.
∴ △ADE 是等边三角形.动脑思考,例题解析 例1 如图,△ABC 是等边三角形,DE∥BC, 分
别交AB,AC 于点D,E.求证:△ADE 是等边三角形. 追问 本题还有其他证法吗? 证明:∵ △ABC 是等边三角形,
∴ ∠A =∠ABC =∠ACB =60°.
∵ DE∥BC,
∴ ∠ABC =∠ADE,
∠ACB =∠AED.
∴ ∠A =∠ADE =∠AED.
∴ △ADE 是等边三角形.动脑思考,变式训练 变式1 若点D、E 在边AB、AC 的延长线上,且
DE∥BC,结论还成立吗? 动脑思考,变式训练 变式2 若点D、E 在边AB、AC 的反向延长线上,
且DE∥BC,结论依然成立吗? 证明: ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.动脑思考,变式训练 练习 完成教科书中的练习.(1)本节课学习了等边三角形的性质和判定;
(2)等边三角形与等腰三角形相比有哪些特殊的性质?
共有几种判定等边三角形的方法?
(3)结合本节课的学习,谈谈研究三角形的方法.课堂小结布置作业教科书习题13.3第12、14题.
和判定的基础上,探索等边三角形的性质和判定方
法.
学习目标:
1.探索等边三角形的性质和判定.
2.能运用等边三角形的性质和判定进行计算和证
明.
学习重点:
探索等边三角形的性质与判定.课件说明 下列图片中有你熟悉的数学图形吗?你能说出此
图形的名称吗?
创设情境,导入新知三条边都相等的三角形是等边三角形. 创设情境,导入新知 问题 满足什么条件的三角形是等边三角形? 联系:等边三角形是特殊的等腰三角形;
区别:等边三角形有三条相等的边,而等腰三角形
只有两条.创设情境,导入新知 请分别画出一个等腰三角形和等边三角形,结合
你画的图形说出它们有什么区别和联系? 思考 将等腰三角形的性质用于等边三角形,你能
得到什么结论?
从边的角度:两腰相等;
从角的角度:等边对等角;
从对称性的角度:轴对称图形、三线合一.细心观察,探索性质 问题 等腰三角形有哪些特殊的性质呢? 细心观察,探索性质 结合等腰三角形的性质,你能填出等边三角形对应
的结论吗? 细心观察,探索性质 结合等腰三角形的性质,你能填出等边三角形对应
的结论吗? 相等
每个角都等于60° 相等
每个角都等于60°细心观察,探索性质 结合等腰三角形的性质,你能填出等边三角形对应
的结论吗? 是(三线合一)
三条对称轴 对“等边三角形的三个内角都相等,并且每一个角
都等于60°”这一结论进行证明.细心观察,探索性质
证明:∵ △ABC 是等边三角形,
∴ BC =AC,BC =AB.
∴ ∠A =∠B,∠A =∠C .
∴ ∠A =∠B =∠C .
∵ ∠A +∠B +∠C =180°,
∴ ∠A =60°.
∴ ∠A =∠B =∠C =60°.细心观察,探索性质 已知:△ABC 是等边三角形 求证:∠A =∠B =∠C
=60°. 符号语言:
∵ △ABC 是等边三角形,
∴ ∠A =∠B =∠C =60°.细心观察,探索性质 等边三角形的性质:
等边三角形的三个内角都相等,并且每一个角都等
于60°.细心观察,探索性质 思考 利用所学知识判断,等边三角形是轴对称图形吗?若是轴对称图形,请画出它的对称轴.
思考1 一个三角形的三个内角满足什么条件是等
边三角形? 三个角都相等的三角形或者一个角为60°的等腰三
角形. 思考2 一个等腰三角形满足什么条件是等边三角
形?细心观察,探索性质 问题 等边三角形除了用定义(即用边)来判定以
外,能否利用角来判定呢?细心观察,探索性质 请你将得到的这两个命题进行证明. 一般三角形 证明:∵ ∠A =∠B,∠B =∠C ,
∴ BC =AC, AC =AB.
∴ AB =BC =AC.
∴ △ABC 是等边三角形. 已知:在△ABC 中,∠A=∠B=∠C.求证:△ABC
是等边三角形.细心观察,探索性质细心观察,探索性质 已知:在△ABC 中,AC =BC且∠A =60°.求证:
△ABC是等边三角形.证明:略. 符号语言:
在△ABC 中,
∵ ∠A=∠B =∠C ,
∴ △ABC 是等边三角形.细心观察,探索性质 等边三角形的判定定理1:
三个角都相等的三角形是等边三角形. 细心观察,探索性质 等边三角形的判定定理2:
有一个角为60°的等腰三角形是等边三角形. 符号语言:
在△ABC 中,
∵ BC =AC,∠A =60°,
∴ △ABC 是等边三角形. 等边三角形的判定定理1:
三个角都相等的三角形是等边三角形.
等边三角形的判定定理2:
有一个角为60°的等腰三角形. 细心观察,概括归纳 判定等边三角形的方法:
从边的角度:等边三角形的定义;
从角的角度:等边三角形的两条判定定理. 证明: ∵ △ABC 是等边三角形,
∴ ∠A =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠ADE,∠C =∠AED.
∴ ∠A=∠ADE =∠AED.
∴ △ADE 是等边三角形.动脑思考,例题解析 例1 如图,△ABC 是等边三角形,DE∥BC, 分
别交AB,AC 于点D,E.求证:△ADE 是等边三角形. 追问 本题还有其他证法吗? 证明:∵ △ABC 是等边三角形,
∴ ∠A =∠ABC =∠ACB =60°.
∵ DE∥BC,
∴ ∠ABC =∠ADE,
∠ACB =∠AED.
∴ ∠A =∠ADE =∠AED.
∴ △ADE 是等边三角形.动脑思考,变式训练 变式1 若点D、E 在边AB、AC 的延长线上,且
DE∥BC,结论还成立吗? 动脑思考,变式训练 变式2 若点D、E 在边AB、AC 的反向延长线上,
且DE∥BC,结论依然成立吗? 证明: ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.动脑思考,变式训练 练习 完成教科书中的练习.(1)本节课学习了等边三角形的性质和判定;
(2)等边三角形与等腰三角形相比有哪些特殊的性质?
共有几种判定等边三角形的方法?
(3)结合本节课的学习,谈谈研究三角形的方法.课堂小结布置作业教科书习题13.3第12、14题.
