2023年四川省内江市中考数学仿真模拟试题(含答案)
文档属性
| 名称 | 2023年四川省内江市中考数学仿真模拟试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 13:54:48 | ||
图片预览




文档简介
四川省内江市2023年中考数学仿真模拟试题
班级: 学号: 姓名: 成绩:
本试卷分为A卷和B卷两部分,A卷满分100分;B卷满分60分、全卷满分160分,120分钟完卷。
注意事项:
1、所有试题的答案必须按题号填写在答题卡相应的位置上,在试卷上、草稿纸上答无效;
2、书写潦草或用改正液(纸)涂改的题视为无效或记为0分!
A卷 (共100分)
一、选择题(本大题共12小题,每小题3分,共36分。在每小题给出的九个选项中,只有一项是符合题目要求的。)
1.2023的相反数是( )
A.2023 B. C. D.
2.牡丹自古以来就是中国的国花,被誉为“百花之王”,据估计,我国牡丹栽种数量约为株,用科学记数法表示为(精确到百万位)( )
A. B. C. D.
3.下列运算正确的是( )
A. B. C. D.
4.将两块三角板按如图所示位置摆放,若,点F在AD上,则与的度数差为( )
A. B.° C. D.
5.如图,一棵大树在离地面3m,5m两处折成三段,中间一段恰好与地面平行,大树顶部落在离大树底部6处,则大树折断前的高度是( )
A. B. C. D.
6.梦天实验舱顺利完成转位,标志着中国空间站“T”字基本构型在轨组装完成.小明用5个相同的小正方体搭成中国空间站的形象,如图所示,这个图形的左视图为( )
A. B. C. D.
7.如图,将△ABC绕点旋转得到,若点A的坐标为,则点的坐标为( )
A. B. C. D.
8.一组数据:1,3,3,5,若添加一个数据3,则发生变化的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
9.如图,为半圆的直径,且,半圆绕点B顺时针旋转.点A旋转到的位置,则图中阴影部分的面积为( )
A. B. C. D.
10.在平面直角坐标系中,点关于轴的对称点的坐标为( )
A. B. C. D.
11.如图,点A是第一像限内反比例函数图像上的一点,轴,垂足为点B,点C在x轴上,△ABC的面积是4,则k 的值等于( )
A.7 B.8 C.9 D.10
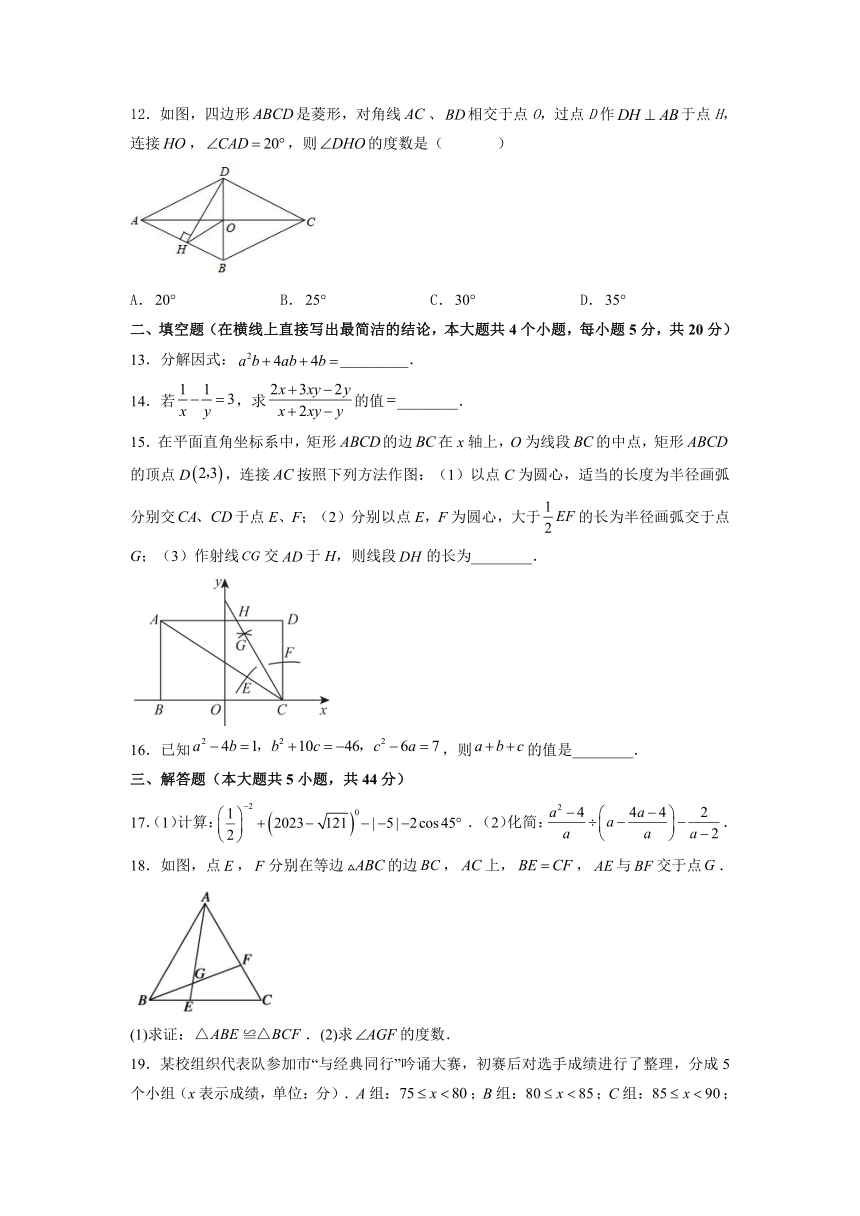
12.如图,四边形是菱形,对角线、相交于点O,过点D作于点H,连接,,则的度数是( )
A. B. C. D.
二、填空题(在横线上直接写出最简洁的结论,本大题共4个小题,每小题5分,共20分)
13.分解因式:_________.
14.若,求的值________.
15.在平面直角坐标系中,矩形的边在x轴上,O为线段的中点,矩形的顶点D,连接按照下列方法作图:(1)以点C为圆心,适当的长度为半径画弧分别交于点E、F;(2)分别以点E,F为圆心,大于的长为半径画弧交于点G;(3)作射线交于H,则线段的长为________.
16.已知,则的值是________.
三、解答题(本大题共5小题,共44分)
17.(1)计算:. (2)化简:.
18.如图,点,分别在等边的边,上,,与交于点.
(1)求证:.(2)求的度数.
19.某校组织代表队参加市“与经典同行”吟诵大赛,初赛后对选手成绩进行了整理,分成5个小组(x表示成绩,单位:分).A组:;B组:;C组:;D组:;E组:,并绘制如下两幅不完整的统计图:请根据图中信息,解答下列问题:
(1)参加初赛的选手共有__________名,请补全频数分布直方图;
(2)扇形统计图中,C组对应的圆心角是多少度?E组人数占参赛选手的百分比是多少?
(3)学校准备组成8人的代表队参加市级决赛,E组6名选手直接进入代表队,现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中两名女生的概率.
20.随着时代的发展和人们生活水平的提高,私家车越来越多,停车越来越难,停车场的建造就成为解决问题的途径之一.如图是一个新建的地下停车场的设计示意图,已知坡道的坡比,,,的长为米,的长为米.按规定,停车场坡道口上方需张贴限高标志,以便告知停车人其车辆能否安全驶入,请根据所给数据,确定该停车场入口的限高,即的长为多少?
21.如图,已知 是一次函数和反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求方程的解是 ;(请根据图象直接写出答案)
(3)求不等式的解集即当一次函数的值小于反比例函数的值时x的取值范围是 ;(请根据图象直接写出答案)
(4)求直线和x轴的交点C的坐标及的面积.
四川省内江市二○二三年高中招生考试暨初中毕业会考全真模拟
数学试题(一)
B卷(共60分)
一、填空题(本大题共4小题,每小题6分,共24分。)
22.已知,则_____.
23.已知二次函数的图像如图所示,有5个结论:①;②;③;④;⑤,其中正确的有是______.
24.如图,在边长为的正方形中,点是边的中点,、分别是和边上的点,则四边形周长的最小值为______.
25.如图,已知在Rt△ABC中,,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD,PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2022个内接正方形的边长为______.
二、解答题(本大题共3小题,每小题12分,共36分。解答时必须写处必要的文字说明、证明过程或推演步骤。)
26、(本小题满分12分)阅读材料:我们学习了《二次根式》和《乘法公式》,可以发现:当,时,有,,当且仅当时取等号.
请利用上述结论解决以下问题:
(1)当时,的最小值为_________;当时,的最大值为_________;
(2)当时,求的最小值;
(3)如图,四边形的对角线、相交于点O,、的面积分别为9和16,求四边形的最小面积.
27、(本小题满分12分)如图,四边形内接于⊙O,为直径,,过点C作于点E,交的延长线于点H,连接交于点G.
(1)求证:是⊙O的切线:(2)若点D为的中点,求证:;(3)若,,求的长.
28、(本小题满分12分)如图,在平面直角坐标系中,抛物线与轴交于、两点,与轴交于点,且.
(1)试求抛物线的解析式;
(2)直线与轴交于点,与抛物线在第一象限交于点,与直线交于点,记,试求的最大值及此时点的坐标;
(3)在(2)的条件下,m取最大值时,点是轴上的一个动点,点是坐标平面内的一点,是否存在这样的点、,使得以、、、四点组成的四边形是矩形?请直接写出满足条件的点的坐标.
四川省内江市2023年中考数学仿真模拟卷
参考答案
1.B;2.A;3.C;4.A; 5.D; 6.D; 7.D; 8.D; 9.D;10.A;11.C;12.A
13.; 14.3; 15.; 16.
17.(1)解:
;
(2)解:
.
18.(1)证明:∵△ABC是等边三角形,
∴(等边三角形的三条边相等),
(等边三角形的三个角都等于60°),
在△ABE和中
∴;
(2)解:∵,
∴(全等三角形的对应角相等),
∴(三角形的一个外角等于不相邻的两个内角的和),
∴,
∴.
19.(1)(人),(人).
(2)C组对应的圆心角度数是:;
E组人数占参赛选手的百分比是:;
(3)画树状图得:
共有12种等可能的结果,抽取的两人恰好是两名女生的有2种结果,
抽取的两人恰好是两名女生的概率为.
20.解:延长交于点E,
∵坡道的坡比,与地面互相平行,
∴,
∵米,
∴,解得:米,
∵米,
∴米,
∵,
∴,
∵,
∴,
∴,
∴,
设,,
根据勾股定理可得:,
即,解得:,
∴米.
答:长为米.
21.(1)把代入,得:
∴
故反比例函数的解析式为:
又把代入,得:
再把, 代入,得:
解得:
故一次函数的解析式为:
(2)方程的解是两图象交点的横坐标,
观察图象得:或;
(3)求不等式的解集即求
当一次函数的值小于反比例函数的值时x的取值范围是
或;
(4)令,则
∴
∴C,即
∴
22.9
【详解】解:∵
∴
∴
∴===9
2.③④⑤
【详解】∵抛物线的开口向下,
∴,
∵,
∴,
∵抛物线与轴的交点在轴的上方,
∴,
∴,
∴结论①错误;
∵当时,,即,
∴结论②错误;
∵当和时,函数值相等,均小于0,
∴,
∴结论③正确;
∵,
∴,
∵由时,得,即,
∴结论④正确;
∴由图象知当时函数取得最大值,
∴,即,
∴结论⑤正确.
3.
【详解】作点关于的对称点,作点关于的对称点,连接
,
,
,
四边形的周长的最小值,
正方形的边长为
,,,
,
四边形的周长的最小值为.
故答案为:.
4.
【详解】解:∵在Rt△ABC中,,
∴∠B=∠C=45°,,
∵在△ABC内作第一个内接正方形DEFG,
∴EF=EC=DG=BD,
∴,∴DE=2,
∵取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,
∴,∴
又∵,
∴
∴,∴,
∵DH=EI,∴,则第n个内接正方形的边长为:,
∴则第2022个内接正方形的边长为.
故答案为:.
5.(1)解:∵当时,,即,
∴的最小值为2;
∵当时,,
∴,即,
∴,
∴,
∴的最大值为;
故答案为:2;;
(2)解:,
,
,
∴当时,y的最小值为11.
(3)解:设,已知,,则由等高三角形性质可知, ,
∴,
,
因此四边形的面积,
当且仅当时取等号,即四边形面积的最小值为49 .
6.(1)证明:如图,连接,
,
,
∵OD=OA,
,
,
,即,
,
,
,
,
是⊙O的切线;
(2)证明:如图,连接,
又,
,
,
又,
,
在和中,
,,
,
点为的中点,
,
;
(3)解:如图,延长交⊙O于点,
是⊙O的直径,,
,
,
,
在中,,即,
,
,
,
,
,
,即,
,
,
在中,,
.
7.(1)解:,
,
,
,
,
抛物线经过点,,,
,解得:,该抛物线的解析式为;
(2)解:如图1,过点作轴交直线于,连接,
设直线的解析式为,
,,
,解得:,
直线的解析式为,
设,则,
,
直线与轴交于点,
,
,
轴,即,
,
,
,
,
,
当时,取得最大值,此时点的坐标为;
(3)解:存在这样的点、,使得以、、、四点组成的四边形是矩形.
①当是矩形的边时,有两种情形,
a、如图2﹣1中,四边形是矩形时,
由(2)可知,代入中,得到,
直线的解析式为,可得,,
由可得,
,
,
,
.
根据矩形的性质,将点向右平移个单位,向下平移1个单位得到点,
,即,
b、如图2﹣2中,四边形是矩形时,
直线的解析式为,,
直线的解析式为,
,
根据矩形的性质可知,将点D向右平移6个单位,向下平移4个单位得到点N,
,即.
②当是对角线时,设,则,,,
是直角顶点,
,
,整理得,方程无解,此种情形不存在,
综上所述,满足条件的的坐标为或.
班级: 学号: 姓名: 成绩:
本试卷分为A卷和B卷两部分,A卷满分100分;B卷满分60分、全卷满分160分,120分钟完卷。
注意事项:
1、所有试题的答案必须按题号填写在答题卡相应的位置上,在试卷上、草稿纸上答无效;
2、书写潦草或用改正液(纸)涂改的题视为无效或记为0分!
A卷 (共100分)
一、选择题(本大题共12小题,每小题3分,共36分。在每小题给出的九个选项中,只有一项是符合题目要求的。)
1.2023的相反数是( )
A.2023 B. C. D.
2.牡丹自古以来就是中国的国花,被誉为“百花之王”,据估计,我国牡丹栽种数量约为株,用科学记数法表示为(精确到百万位)( )
A. B. C. D.
3.下列运算正确的是( )
A. B. C. D.
4.将两块三角板按如图所示位置摆放,若,点F在AD上,则与的度数差为( )
A. B.° C. D.
5.如图,一棵大树在离地面3m,5m两处折成三段,中间一段恰好与地面平行,大树顶部落在离大树底部6处,则大树折断前的高度是( )
A. B. C. D.
6.梦天实验舱顺利完成转位,标志着中国空间站“T”字基本构型在轨组装完成.小明用5个相同的小正方体搭成中国空间站的形象,如图所示,这个图形的左视图为( )
A. B. C. D.
7.如图,将△ABC绕点旋转得到,若点A的坐标为,则点的坐标为( )
A. B. C. D.
8.一组数据:1,3,3,5,若添加一个数据3,则发生变化的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
9.如图,为半圆的直径,且,半圆绕点B顺时针旋转.点A旋转到的位置,则图中阴影部分的面积为( )
A. B. C. D.
10.在平面直角坐标系中,点关于轴的对称点的坐标为( )
A. B. C. D.
11.如图,点A是第一像限内反比例函数图像上的一点,轴,垂足为点B,点C在x轴上,△ABC的面积是4,则k 的值等于( )
A.7 B.8 C.9 D.10
12.如图,四边形是菱形,对角线、相交于点O,过点D作于点H,连接,,则的度数是( )
A. B. C. D.
二、填空题(在横线上直接写出最简洁的结论,本大题共4个小题,每小题5分,共20分)
13.分解因式:_________.
14.若,求的值________.
15.在平面直角坐标系中,矩形的边在x轴上,O为线段的中点,矩形的顶点D,连接按照下列方法作图:(1)以点C为圆心,适当的长度为半径画弧分别交于点E、F;(2)分别以点E,F为圆心,大于的长为半径画弧交于点G;(3)作射线交于H,则线段的长为________.
16.已知,则的值是________.
三、解答题(本大题共5小题,共44分)
17.(1)计算:. (2)化简:.
18.如图,点,分别在等边的边,上,,与交于点.
(1)求证:.(2)求的度数.
19.某校组织代表队参加市“与经典同行”吟诵大赛,初赛后对选手成绩进行了整理,分成5个小组(x表示成绩,单位:分).A组:;B组:;C组:;D组:;E组:,并绘制如下两幅不完整的统计图:请根据图中信息,解答下列问题:
(1)参加初赛的选手共有__________名,请补全频数分布直方图;
(2)扇形统计图中,C组对应的圆心角是多少度?E组人数占参赛选手的百分比是多少?
(3)学校准备组成8人的代表队参加市级决赛,E组6名选手直接进入代表队,现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中两名女生的概率.
20.随着时代的发展和人们生活水平的提高,私家车越来越多,停车越来越难,停车场的建造就成为解决问题的途径之一.如图是一个新建的地下停车场的设计示意图,已知坡道的坡比,,,的长为米,的长为米.按规定,停车场坡道口上方需张贴限高标志,以便告知停车人其车辆能否安全驶入,请根据所给数据,确定该停车场入口的限高,即的长为多少?
21.如图,已知 是一次函数和反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求方程的解是 ;(请根据图象直接写出答案)
(3)求不等式的解集即当一次函数的值小于反比例函数的值时x的取值范围是 ;(请根据图象直接写出答案)
(4)求直线和x轴的交点C的坐标及的面积.
四川省内江市二○二三年高中招生考试暨初中毕业会考全真模拟
数学试题(一)
B卷(共60分)
一、填空题(本大题共4小题,每小题6分,共24分。)
22.已知,则_____.
23.已知二次函数的图像如图所示,有5个结论:①;②;③;④;⑤,其中正确的有是______.
24.如图,在边长为的正方形中,点是边的中点,、分别是和边上的点,则四边形周长的最小值为______.
25.如图,已知在Rt△ABC中,,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD,PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2022个内接正方形的边长为______.
二、解答题(本大题共3小题,每小题12分,共36分。解答时必须写处必要的文字说明、证明过程或推演步骤。)
26、(本小题满分12分)阅读材料:我们学习了《二次根式》和《乘法公式》,可以发现:当,时,有,,当且仅当时取等号.
请利用上述结论解决以下问题:
(1)当时,的最小值为_________;当时,的最大值为_________;
(2)当时,求的最小值;
(3)如图,四边形的对角线、相交于点O,、的面积分别为9和16,求四边形的最小面积.
27、(本小题满分12分)如图,四边形内接于⊙O,为直径,,过点C作于点E,交的延长线于点H,连接交于点G.
(1)求证:是⊙O的切线:(2)若点D为的中点,求证:;(3)若,,求的长.
28、(本小题满分12分)如图,在平面直角坐标系中,抛物线与轴交于、两点,与轴交于点,且.
(1)试求抛物线的解析式;
(2)直线与轴交于点,与抛物线在第一象限交于点,与直线交于点,记,试求的最大值及此时点的坐标;
(3)在(2)的条件下,m取最大值时,点是轴上的一个动点,点是坐标平面内的一点,是否存在这样的点、,使得以、、、四点组成的四边形是矩形?请直接写出满足条件的点的坐标.
四川省内江市2023年中考数学仿真模拟卷
参考答案
1.B;2.A;3.C;4.A; 5.D; 6.D; 7.D; 8.D; 9.D;10.A;11.C;12.A
13.; 14.3; 15.; 16.
17.(1)解:
;
(2)解:
.
18.(1)证明:∵△ABC是等边三角形,
∴(等边三角形的三条边相等),
(等边三角形的三个角都等于60°),
在△ABE和中
∴;
(2)解:∵,
∴(全等三角形的对应角相等),
∴(三角形的一个外角等于不相邻的两个内角的和),
∴,
∴.
19.(1)(人),(人).
(2)C组对应的圆心角度数是:;
E组人数占参赛选手的百分比是:;
(3)画树状图得:
共有12种等可能的结果,抽取的两人恰好是两名女生的有2种结果,
抽取的两人恰好是两名女生的概率为.
20.解:延长交于点E,
∵坡道的坡比,与地面互相平行,
∴,
∵米,
∴,解得:米,
∵米,
∴米,
∵,
∴,
∵,
∴,
∴,
∴,
设,,
根据勾股定理可得:,
即,解得:,
∴米.
答:长为米.
21.(1)把代入,得:
∴
故反比例函数的解析式为:
又把代入,得:
再把, 代入,得:
解得:
故一次函数的解析式为:
(2)方程的解是两图象交点的横坐标,
观察图象得:或;
(3)求不等式的解集即求
当一次函数的值小于反比例函数的值时x的取值范围是
或;
(4)令,则
∴
∴C,即
∴
22.9
【详解】解:∵
∴
∴
∴===9
2.③④⑤
【详解】∵抛物线的开口向下,
∴,
∵,
∴,
∵抛物线与轴的交点在轴的上方,
∴,
∴,
∴结论①错误;
∵当时,,即,
∴结论②错误;
∵当和时,函数值相等,均小于0,
∴,
∴结论③正确;
∵,
∴,
∵由时,得,即,
∴结论④正确;
∴由图象知当时函数取得最大值,
∴,即,
∴结论⑤正确.
3.
【详解】作点关于的对称点,作点关于的对称点,连接
,
,
,
四边形的周长的最小值,
正方形的边长为
,,,
,
四边形的周长的最小值为.
故答案为:.
4.
【详解】解:∵在Rt△ABC中,,
∴∠B=∠C=45°,,
∵在△ABC内作第一个内接正方形DEFG,
∴EF=EC=DG=BD,
∴,∴DE=2,
∵取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,
∴,∴
又∵,
∴
∴,∴,
∵DH=EI,∴,则第n个内接正方形的边长为:,
∴则第2022个内接正方形的边长为.
故答案为:.
5.(1)解:∵当时,,即,
∴的最小值为2;
∵当时,,
∴,即,
∴,
∴,
∴的最大值为;
故答案为:2;;
(2)解:,
,
,
∴当时,y的最小值为11.
(3)解:设,已知,,则由等高三角形性质可知, ,
∴,
,
因此四边形的面积,
当且仅当时取等号,即四边形面积的最小值为49 .
6.(1)证明:如图,连接,
,
,
∵OD=OA,
,
,
,即,
,
,
,
,
是⊙O的切线;
(2)证明:如图,连接,
又,
,
,
又,
,
在和中,
,,
,
点为的中点,
,
;
(3)解:如图,延长交⊙O于点,
是⊙O的直径,,
,
,
,
在中,,即,
,
,
,
,
,
,即,
,
,
在中,,
.
7.(1)解:,
,
,
,
,
抛物线经过点,,,
,解得:,该抛物线的解析式为;
(2)解:如图1,过点作轴交直线于,连接,
设直线的解析式为,
,,
,解得:,
直线的解析式为,
设,则,
,
直线与轴交于点,
,
,
轴,即,
,
,
,
,
,
当时,取得最大值,此时点的坐标为;
(3)解:存在这样的点、,使得以、、、四点组成的四边形是矩形.
①当是矩形的边时,有两种情形,
a、如图2﹣1中,四边形是矩形时,
由(2)可知,代入中,得到,
直线的解析式为,可得,,
由可得,
,
,
,
.
根据矩形的性质,将点向右平移个单位,向下平移1个单位得到点,
,即,
b、如图2﹣2中,四边形是矩形时,
直线的解析式为,,
直线的解析式为,
,
根据矩形的性质可知,将点D向右平移6个单位,向下平移4个单位得到点N,
,即.
②当是对角线时,设,则,,,
是直角顶点,
,
,整理得,方程无解,此种情形不存在,
综上所述,满足条件的的坐标为或.
同课章节目录
