沪科版九年级数学上册第22章相似三角形综合测试卷 (含答案)
文档属性
| 名称 | 沪科版九年级数学上册第22章相似三角形综合测试卷 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 275.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 14:03:13 | ||
图片预览


文档简介
沪科版九上第22章相似三角形综合测试卷
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
一、选择题
已知2x=3y(xy≠0),那么下列比例式中成立的是( )
A. = B. = C. = D. =
在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一栋楼的影长为90m,则这栋楼的高度为( )
A. 54m B. 135m C. 150m D. 162m
如图,BE是△ABC的中线,点F在BE上,延长AF交BC于点D,若BF=3EF,则=( )
A.
B.
C.
D.
如图,AB∥CD∥EF,AF交BE于点G,若AC=CG,AG=FG,则下列结论错误的是( )
A.
B.
C.
D.
如图,在△ABC中,点D为BC边上的一点,且AD=AB=2,AD⊥AB,过点D作DE⊥AD,DE交AC于点E,若DE=1,则△ABC的面积为()
A. B. 4 C. D. 8
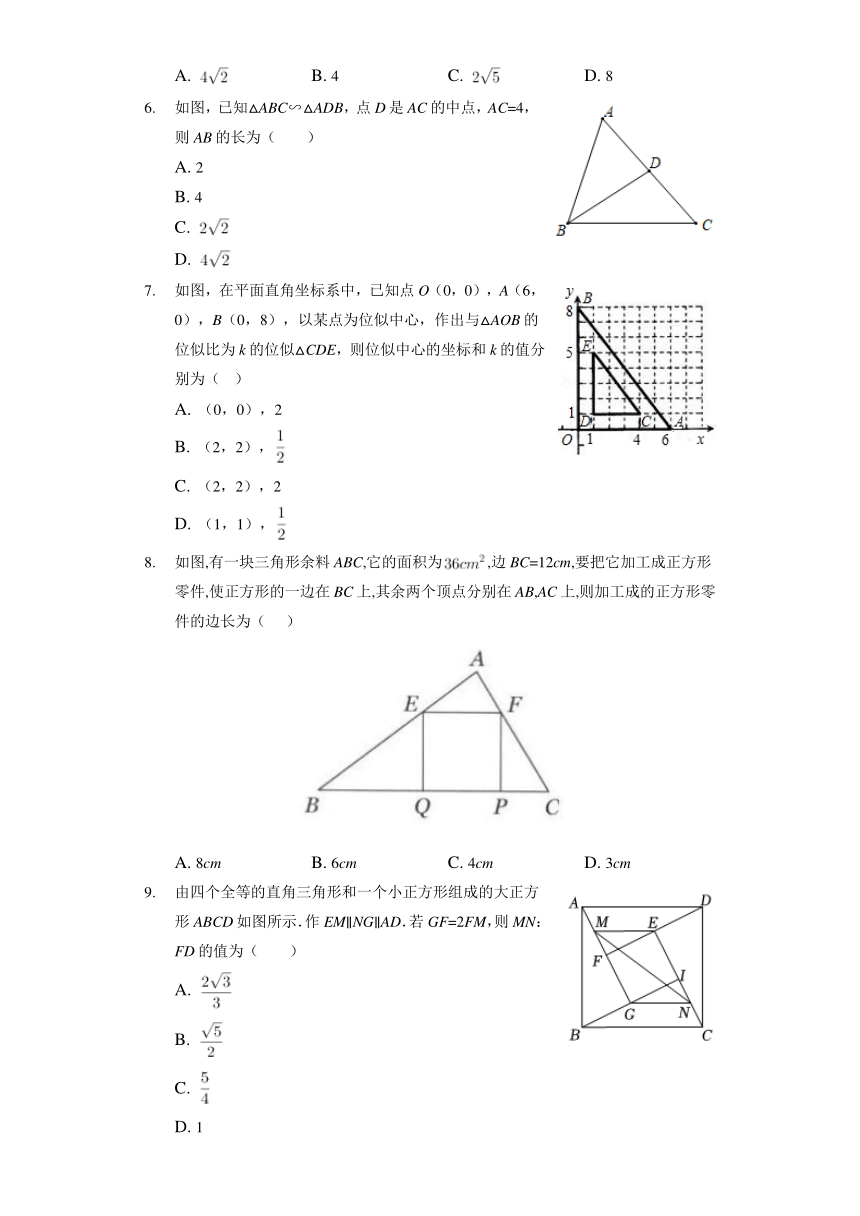
如图,已知△ABC∽△ADB,点D是AC的中点,AC=4,则AB的长为( )
A. 2
B. 4
C.
D.
如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为( )
A. (0,0),2
B. (2,2),
C. (2,2),2
D. (1,1),
如图,有一块三角形余料ABC,它的面积为,边BC=12cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则加工成的正方形零件的边长为( )
A. 8cm B. 6cm C. 4cm D. 3cm
由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.作EM∥NG∥AD.若GF=2FM,则MN:FD的值为( )
A.
B.
C.
D. 1
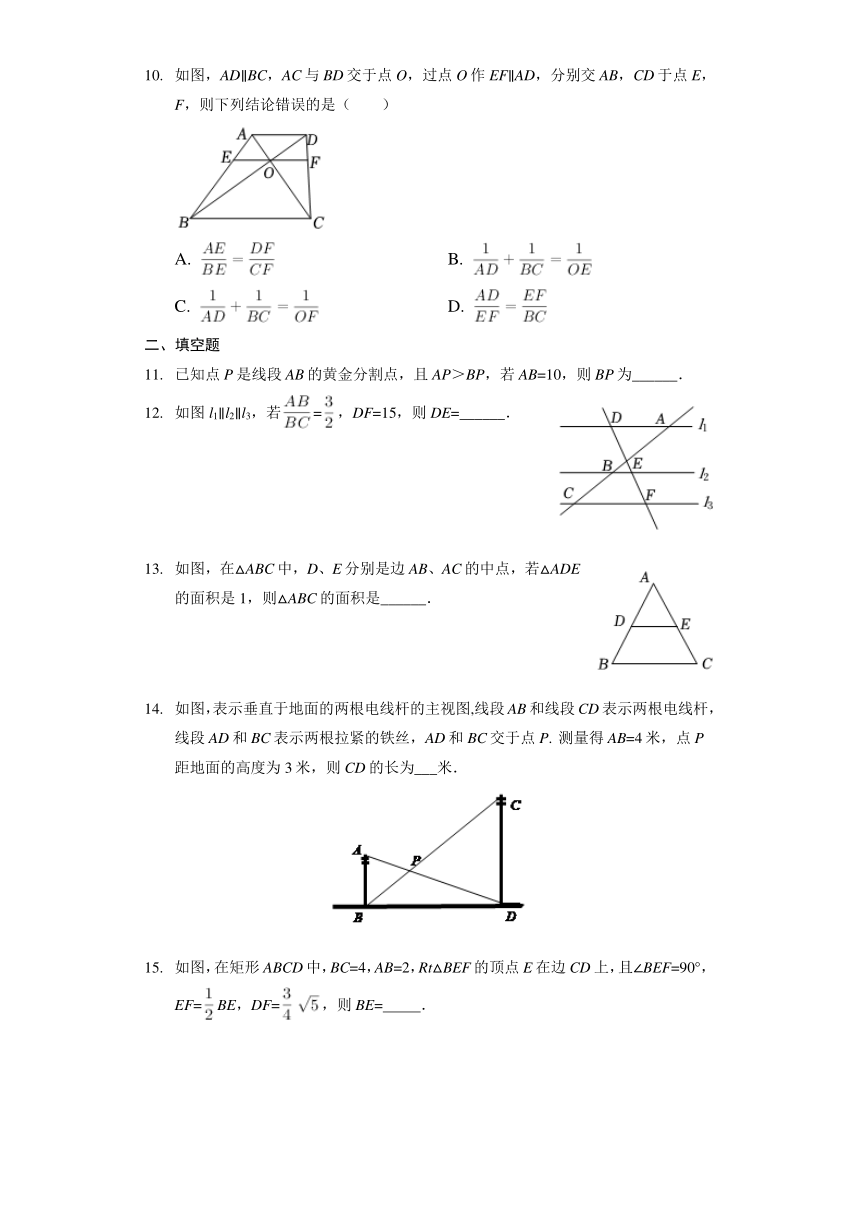
如图,AD∥BC,AC与BD交于点O,过点O作EF∥AD,分别交AB,CD于点E,F,则下列结论错误的是( )
A. B.
C. D.
二、填空题
已知点P是线段AB的黄金分割点,且AP>BP,若AB=10,则BP为______.
如图l1∥l2∥l3,若=,DF=15,则DE=______.
如图,在△ABC中,D、E分别是边AB、AC的中点,若△ADE的面积是1,则△ABC的面积是______.
如图,表示垂直于地面的两根电线杆的主视图,线段AB和线段CD表示两根电线杆,线段AD和BC表示两根拉紧的铁丝,AD和BC交于点P. 测量得AB=4米,点P距地面的高度为3米,则CD的长为___米.
如图,在矩形ABCD中,BC=4,AB=2,Rt△BEF的顶点E在边CD上,且∠BEF=90°,EF=BE,DF=,则BE= .
三、解答题
已知线段a=0.3m,b=60cm,c=12dm.
(1)求线段a与线段b的比.
(2)如果线段a、b、c、d成比例,求线段d的长.
(3)b是a和c的比例中项吗?为什么?
已知,如图l1∥l2∥l3,若AB=6,BC=10,DF=24,求DE和EF的长.
如图,在平面直角坐标系中,已知ABC的三个顶点坐标是A(0,-2),B(6,-4),C(2,-6).
(1)请画出与ABC关于x轴对称的.
(2)以点为位似中心,将ABC缩小为原来的,得到,请在y轴左侧画出.
(3)在y轴上存在点P,使得的面积为6,请直接写出满足条件的点P的坐标.
如图,小华站在两栋楼AB、CD间线段AC的中点F处,调整帽檐使视线通过帽檐边沿正好看到楼AB的顶端点B,她保持身体姿势不变,向着楼AB的方向走去,当她到达楼AB的底端A处时,原地转身,视线通过帽檐边沿正好看到大楼CD的顶端点D,已知楼AB的高度为7米,小华眼睛距离地面的高度EF为1.5米,请你计算大楼CD的高度.
△ABC中,∠BAC是直角,过斜边中点M而垂直于斜边BC的直线交CA的延长线于E,交AB于D,连AM.
求证:(1)△ABC∽△MEC;
(2)AM2=MD ME.
如图1,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD.EC与BD相交于点G,与AD相交于点F,AF=AB.
(1)求证:BD⊥EC;
(2)若AB=1,求AE的长;
(3)如图2,连接AG,求证:EG-DG=AG.
1.B 2.A 3.B 4.B 5.B 6.C 7.B 8.C 9.B 10.D
11.15-10
12.9
13.4
14.12
15.
16.解:(1)∵a=0.3m=30cm;b=60cm,
∴a:b=30:60=1:2;
(2)∵线段a、b、c、d是成比例线段,
∴=,
∵c=12dm=120cm,
∴=,
∴d=240cm;
(3)是,理由:
∵b2=3600,ac=30×120=3600,
∴b2=ac,
∴b是a和c的比例中项.
17.解:∵l1∥l2∥l3,
∴=,
∵AB=6,BC=10,DF=24,
∴=,
解得:DE=9,
∴EF=24-9=15.
18.解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)如图所示:当△OB2P的面积为6时,点P的坐标为:(0,4),(0,-4).
19.解:如图,延长ME交CD于点N,
由题意得:AM=EF=CN=1.5米,ME=EN=MN,∠BEM=∠DMN,∠BME=∠DNM=90°,
∴△BME∽△DNM,
∴,
∵AB=7米,
∴BM=AB-AM=7-1.5=5.5(米),
∴,
解得:DN=11,
∴CD=CN+DN=1.5+11=12.5(米),
答:大楼CD的高度为12.5米.
20.证明:(1)∵∠BAC是直角,ME⊥BC,
∴∠BAC=∠EMC=90°,
∵∠C=∠C,
∴△ABC∽△MEC;
(2)∵∠BAC是直角,ME⊥BC,
∴∠C+∠E=∠C+∠B,
∴∠E=∠B,
∵点M为直角△ABC斜边的中点,
∴MA=MB,∠MAD=∠B;
而∠AMD=∠EMA,
∴△MAD∽△MEA.
∴,
∴AM2=MD ME.
21.(1)证明:∵四边形ABCD是矩形,点E在BA的延长线上,
∴∠EAF=∠DAB=90°,
又∵AE=AD,AF=AB,
∴△AEF△ADB(SAS),
∴∠AEF=∠ADB,
∴∠GEB+∠GBE=∠ADB+∠ABD=90°,
即∠EGB=90°,
故BD⊥EC,
(2)解:∵四边形ABCD是矩形,
∴AE∥CD,
∴△AEF∽△DCF,
∴,即AE DF=AF DC,
设AE=AD=a(a>0),则有a (a-1)=1,化简得a2-a-1=0,
解得或(舍去),
∴AE=.
(3)解:如图,在线段EG上取点P,使得EP=DG,
在△AEP与△ADG中,AE=AD,∠AEP=∠ADG,EP=DG,
∴△AEP△ADG(SAS),
∴AP=AG,∠EAP=∠DAG,
∴∠PAG=∠PAD+∠DAG=∠PAD+∠EAP=∠DAE=90°,
∴△PAG为等腰直角三角形,
∴EG-DG=EG-EP=PG=AG.
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
一、选择题
已知2x=3y(xy≠0),那么下列比例式中成立的是( )
A. = B. = C. = D. =
在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一栋楼的影长为90m,则这栋楼的高度为( )
A. 54m B. 135m C. 150m D. 162m
如图,BE是△ABC的中线,点F在BE上,延长AF交BC于点D,若BF=3EF,则=( )
A.
B.
C.
D.
如图,AB∥CD∥EF,AF交BE于点G,若AC=CG,AG=FG,则下列结论错误的是( )
A.
B.
C.
D.
如图,在△ABC中,点D为BC边上的一点,且AD=AB=2,AD⊥AB,过点D作DE⊥AD,DE交AC于点E,若DE=1,则△ABC的面积为()
A. B. 4 C. D. 8
如图,已知△ABC∽△ADB,点D是AC的中点,AC=4,则AB的长为( )
A. 2
B. 4
C.
D.
如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为( )
A. (0,0),2
B. (2,2),
C. (2,2),2
D. (1,1),
如图,有一块三角形余料ABC,它的面积为,边BC=12cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则加工成的正方形零件的边长为( )
A. 8cm B. 6cm C. 4cm D. 3cm
由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.作EM∥NG∥AD.若GF=2FM,则MN:FD的值为( )
A.
B.
C.
D. 1
如图,AD∥BC,AC与BD交于点O,过点O作EF∥AD,分别交AB,CD于点E,F,则下列结论错误的是( )
A. B.
C. D.
二、填空题
已知点P是线段AB的黄金分割点,且AP>BP,若AB=10,则BP为______.
如图l1∥l2∥l3,若=,DF=15,则DE=______.
如图,在△ABC中,D、E分别是边AB、AC的中点,若△ADE的面积是1,则△ABC的面积是______.
如图,表示垂直于地面的两根电线杆的主视图,线段AB和线段CD表示两根电线杆,线段AD和BC表示两根拉紧的铁丝,AD和BC交于点P. 测量得AB=4米,点P距地面的高度为3米,则CD的长为___米.
如图,在矩形ABCD中,BC=4,AB=2,Rt△BEF的顶点E在边CD上,且∠BEF=90°,EF=BE,DF=,则BE= .
三、解答题
已知线段a=0.3m,b=60cm,c=12dm.
(1)求线段a与线段b的比.
(2)如果线段a、b、c、d成比例,求线段d的长.
(3)b是a和c的比例中项吗?为什么?
已知,如图l1∥l2∥l3,若AB=6,BC=10,DF=24,求DE和EF的长.
如图,在平面直角坐标系中,已知ABC的三个顶点坐标是A(0,-2),B(6,-4),C(2,-6).
(1)请画出与ABC关于x轴对称的.
(2)以点为位似中心,将ABC缩小为原来的,得到,请在y轴左侧画出.
(3)在y轴上存在点P,使得的面积为6,请直接写出满足条件的点P的坐标.
如图,小华站在两栋楼AB、CD间线段AC的中点F处,调整帽檐使视线通过帽檐边沿正好看到楼AB的顶端点B,她保持身体姿势不变,向着楼AB的方向走去,当她到达楼AB的底端A处时,原地转身,视线通过帽檐边沿正好看到大楼CD的顶端点D,已知楼AB的高度为7米,小华眼睛距离地面的高度EF为1.5米,请你计算大楼CD的高度.
△ABC中,∠BAC是直角,过斜边中点M而垂直于斜边BC的直线交CA的延长线于E,交AB于D,连AM.
求证:(1)△ABC∽△MEC;
(2)AM2=MD ME.
如图1,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD.EC与BD相交于点G,与AD相交于点F,AF=AB.
(1)求证:BD⊥EC;
(2)若AB=1,求AE的长;
(3)如图2,连接AG,求证:EG-DG=AG.
1.B 2.A 3.B 4.B 5.B 6.C 7.B 8.C 9.B 10.D
11.15-10
12.9
13.4
14.12
15.
16.解:(1)∵a=0.3m=30cm;b=60cm,
∴a:b=30:60=1:2;
(2)∵线段a、b、c、d是成比例线段,
∴=,
∵c=12dm=120cm,
∴=,
∴d=240cm;
(3)是,理由:
∵b2=3600,ac=30×120=3600,
∴b2=ac,
∴b是a和c的比例中项.
17.解:∵l1∥l2∥l3,
∴=,
∵AB=6,BC=10,DF=24,
∴=,
解得:DE=9,
∴EF=24-9=15.
18.解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)如图所示:当△OB2P的面积为6时,点P的坐标为:(0,4),(0,-4).
19.解:如图,延长ME交CD于点N,
由题意得:AM=EF=CN=1.5米,ME=EN=MN,∠BEM=∠DMN,∠BME=∠DNM=90°,
∴△BME∽△DNM,
∴,
∵AB=7米,
∴BM=AB-AM=7-1.5=5.5(米),
∴,
解得:DN=11,
∴CD=CN+DN=1.5+11=12.5(米),
答:大楼CD的高度为12.5米.
20.证明:(1)∵∠BAC是直角,ME⊥BC,
∴∠BAC=∠EMC=90°,
∵∠C=∠C,
∴△ABC∽△MEC;
(2)∵∠BAC是直角,ME⊥BC,
∴∠C+∠E=∠C+∠B,
∴∠E=∠B,
∵点M为直角△ABC斜边的中点,
∴MA=MB,∠MAD=∠B;
而∠AMD=∠EMA,
∴△MAD∽△MEA.
∴,
∴AM2=MD ME.
21.(1)证明:∵四边形ABCD是矩形,点E在BA的延长线上,
∴∠EAF=∠DAB=90°,
又∵AE=AD,AF=AB,
∴△AEF△ADB(SAS),
∴∠AEF=∠ADB,
∴∠GEB+∠GBE=∠ADB+∠ABD=90°,
即∠EGB=90°,
故BD⊥EC,
(2)解:∵四边形ABCD是矩形,
∴AE∥CD,
∴△AEF∽△DCF,
∴,即AE DF=AF DC,
设AE=AD=a(a>0),则有a (a-1)=1,化简得a2-a-1=0,
解得或(舍去),
∴AE=.
(3)解:如图,在线段EG上取点P,使得EP=DG,
在△AEP与△ADG中,AE=AD,∠AEP=∠ADG,EP=DG,
∴△AEP△ADG(SAS),
∴AP=AG,∠EAP=∠DAG,
∴∠PAG=∠PAD+∠DAG=∠PAD+∠EAP=∠DAE=90°,
∴△PAG为等腰直角三角形,
∴EG-DG=EG-EP=PG=AG.
