第7章 平面直角坐标系单元检测题(含答案)
文档属性
| 名称 | 第7章 平面直角坐标系单元检测题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 417.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第七章《平面直角坐标系》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.在直角坐标系中,将点(2,-3)向左平移2个单位长度得到的点的坐标是( )
A.(4,-3) B.(-4,3) C.(0,-3) D.(0,3)
2. 如图,、、这三个点中,在第二象限内的有( )
A.、、 B.、 C.、 D.
第2题图 第3题图
3.如图,矩形的各边分别平行于轴或轴,物体甲和物体乙分别由点(2,0)同时出发,沿矩形的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是( )
A.(2,0) B.(-1,1) C.(-2,1) D.(-1,-1)
4.如图,若在象棋盘上建立平面直角坐标系,使“将”位于点(1,﹣2),“象”位于点(3,﹣2),则“炮”位于点( )
A.(1,3) B.(﹣2,0) C.(﹣1,2) D.(﹣2,2)
5、已知点P(x,y)的坐标满足|x|=3, =2,且xy<0,则点P的坐标是( )
A.(3,-2) B.(-3,2) C.(3,-4) D.(-3,4)
6、已知点A(1,0)B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标
为( )
A.(-4,0) B.(6,0) C.(-4,0)或(6,0) D.(0,12)或(0,-8)
7.已知点A(a﹣2,2a+7),点B的坐标为(1,5),直线AB∥y轴,则a的值是( )
A.1 B.3 C.﹣1 D.5
8.将点A(﹣2,﹣3)向右平移3个单位长度得到点B,则点B所处的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.如图7-12,图①中的圆平移得到图②中的圆,如果图①中圆上一点的坐标为,那么平移后在图②中的对应点的坐标为( )
A. B. C. D.
10.已知线段,且点的坐标为,若轴,则点的坐标为( )
A. B. C.或 D.或
二、填空题(每题3分,共24分)
11.如图是某学校的平面示意图,在10×10的正方形网格中(每个小方格都是边长为1的正方形),如果分别用(3,1),(3,5)表示图中图书馆和教学楼的位置,那么实验楼的位置应表示为
12.A点坐标为(3,1),线段AB=4,且AB//x轴,则B点坐标为
13.已知点P(-6,2)在第一、三象限的角平分线上,则x= ;已知点Q(+2,-11)在第二、四象限的角平分线上,则x=
14.如图,平面直角坐标系中,A、B两点的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,点A1的坐标为(3,1),则点B1的坐标为 .
15、若点P在第二象限,则点Q在第 象限。
16、已知 (,)点在轴的左侧,且││=3,││=2,则点的坐标为 。
17..如图7-15,在平面直角坐标系中,已知,则三角形的面积为________.
18..如图7-16,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位长度,得到点那么点是自然数)的坐标为________(用表示).
三.解答题(46分,第19题6分,20、21、22、23、24每题8分)
19.已知平面直角坐标系中有一点(,).
(1)若点在第四象限,求的取值范围;
(2)若点到轴的距离为3,求点的坐标.
20.如图,已知点A(-2,3),B(4,3),C(-1,-3).
(1)求点C到x轴的距离;
(2)求三角形ABC的面积;
(3)点P在y轴上,当三角形ABP的面积为6时,请直接写出点P的坐标.
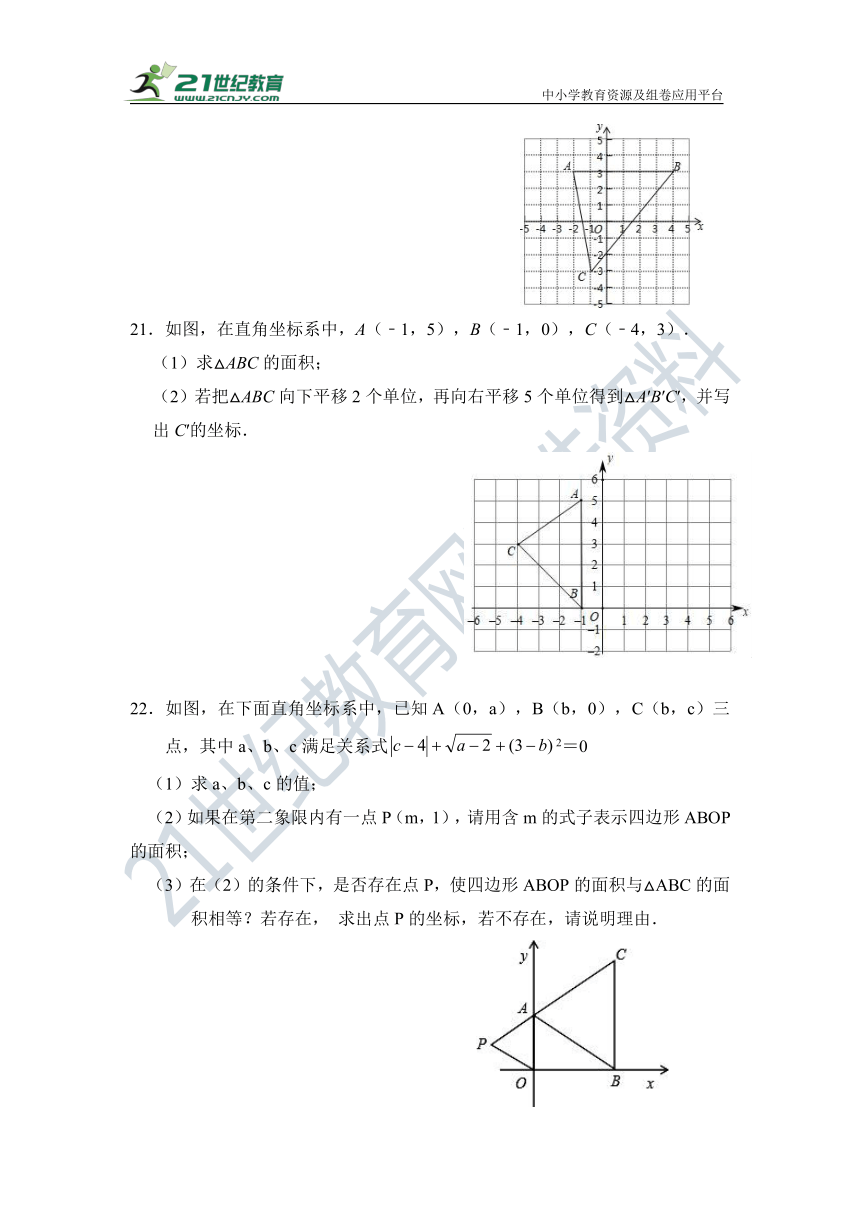
21.如图,在直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求△ABC的面积;
(2)若把△ABC向下平移2个单位,再向右平移5个单位得到△A′B′C′,并写出C′的坐标.
22.如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式2=0
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,1),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在, 求出点P的坐标,若不存在,请说明理由.
23.在如图,所示的平面直角坐标系中描出下列各点:A(0,3),B(5,0),C(3,-5),D(-3,-5),E(3,5).
(1)点A到原点的距离是 ;
(2)将点C向x轴负方向平移6个单位长度后与点 重合;
(3)连接CE,则直线CE与y轴是什么位置关系
(4)点D到x轴,y轴的距离分别是多少
24.如图6,在平面直角坐标系中,三角形ABC的顶点都在格点上,其中,点C的坐标为(1,2).
(1)填空:点A的坐标是 ,点B的坐标是 ;
(2)将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度,得到三角形A'B'C',画出三角形A'B'C',并写出三角形A'B'C'三个顶点的坐标;
(3)求三角形ABC的面积.
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D B D C B D C C
二、填空题:
11.(-3,4)
12.(-1,1)或(7,1)
13.2,
14.【解答】解:∵A、B两点的坐标分别为(2,0)、(0,1),平移后A1(3,1),
∴线段AB向右平移1个单位,向上平移1个单位,
∴a=0+1=1,b=1+1=2,
点B1的坐标为(1,2),
故答案为:(1,2),
15、四
16、(-3,2)或(-3,-2)
17.【答案】5
【解析】由题中图象可知,.
18.【答案】
【解析】由题图可知,当时,,点;当时,,点;当时,,点.所以点的坐标为.
三.解答题:
19.(1)由题意可得:2m+1>0,m-3<0,解得:﹣<m<3;
(2)由题意可得:|2m+1|=3,解得:m=1或m=﹣2.
当m=1时,点P的坐标为(3,-2);
当m=﹣2时,点P的坐标为(﹣3,-5).
综上所述:点P的坐标为(3,﹣2)或(﹣3,-5).
20.解:(1)∵C(-1,-3),
∴|-3|=3,
∴点C到x轴的距离为3;
(2)∵A(-2,3)、B(4,3)、C(-1,-3)
∴AB=4-(-2) =6,点C到边AB的距离为:3-(-3) =6,
∴△ABC的面积为:6×6÷2=18.
(3)设点P的坐标为(0,y),
∵△ABP的面积为6,A(-2,3)、B(4,3),
∴×6×|x 3|=6,
∴|x-3|=2,
∴x=5或x=1,
∴P点的坐标为(0,5)或(0,1).
21.【分析】(1)根据三角形面积求法得出即可;
(2)根据已知将△ABC各顶点向下平移2个单位,向右平移5个单位得到各对应点,即可作图;进而得出点C′的坐标.
【解答】解:(1)△ABC的面积是:×3×5=7.5;
(2)作图如下:
∴点C′的坐标为:(1,1).
【点评】此题主要考查了平移变换以及三角形面积求法,正确平移图象的各顶点坐标是解题关键.
22.(1)a=2、b=3、c=4; (2)3 – m; (3)P(-3,1);
23..解:如图.
(1)3
(2)D
(3)直线CE与y轴平行.
(4)点D到x轴的距离是5,到y轴的距离是3.
24.解:(1)(2,-1) (4,3)
(2)如图,三角形A'B'C'即为所求作的图形;A'(0,0),B'(2,4),C'(-1,3).
(3)三角形ABC的面积为
3×4-×2×4-×3×1-×3×1=5.
www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
第七章《平面直角坐标系》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.在直角坐标系中,将点(2,-3)向左平移2个单位长度得到的点的坐标是( )
A.(4,-3) B.(-4,3) C.(0,-3) D.(0,3)
2. 如图,、、这三个点中,在第二象限内的有( )
A.、、 B.、 C.、 D.
第2题图 第3题图
3.如图,矩形的各边分别平行于轴或轴,物体甲和物体乙分别由点(2,0)同时出发,沿矩形的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是( )
A.(2,0) B.(-1,1) C.(-2,1) D.(-1,-1)
4.如图,若在象棋盘上建立平面直角坐标系,使“将”位于点(1,﹣2),“象”位于点(3,﹣2),则“炮”位于点( )
A.(1,3) B.(﹣2,0) C.(﹣1,2) D.(﹣2,2)
5、已知点P(x,y)的坐标满足|x|=3, =2,且xy<0,则点P的坐标是( )
A.(3,-2) B.(-3,2) C.(3,-4) D.(-3,4)
6、已知点A(1,0)B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标
为( )
A.(-4,0) B.(6,0) C.(-4,0)或(6,0) D.(0,12)或(0,-8)
7.已知点A(a﹣2,2a+7),点B的坐标为(1,5),直线AB∥y轴,则a的值是( )
A.1 B.3 C.﹣1 D.5
8.将点A(﹣2,﹣3)向右平移3个单位长度得到点B,则点B所处的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.如图7-12,图①中的圆平移得到图②中的圆,如果图①中圆上一点的坐标为,那么平移后在图②中的对应点的坐标为( )
A. B. C. D.
10.已知线段,且点的坐标为,若轴,则点的坐标为( )
A. B. C.或 D.或
二、填空题(每题3分,共24分)
11.如图是某学校的平面示意图,在10×10的正方形网格中(每个小方格都是边长为1的正方形),如果分别用(3,1),(3,5)表示图中图书馆和教学楼的位置,那么实验楼的位置应表示为
12.A点坐标为(3,1),线段AB=4,且AB//x轴,则B点坐标为
13.已知点P(-6,2)在第一、三象限的角平分线上,则x= ;已知点Q(+2,-11)在第二、四象限的角平分线上,则x=
14.如图,平面直角坐标系中,A、B两点的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,点A1的坐标为(3,1),则点B1的坐标为 .
15、若点P在第二象限,则点Q在第 象限。
16、已知 (,)点在轴的左侧,且││=3,││=2,则点的坐标为 。
17..如图7-15,在平面直角坐标系中,已知,则三角形的面积为________.
18..如图7-16,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位长度,得到点那么点是自然数)的坐标为________(用表示).
三.解答题(46分,第19题6分,20、21、22、23、24每题8分)
19.已知平面直角坐标系中有一点(,).
(1)若点在第四象限,求的取值范围;
(2)若点到轴的距离为3,求点的坐标.
20.如图,已知点A(-2,3),B(4,3),C(-1,-3).
(1)求点C到x轴的距离;
(2)求三角形ABC的面积;
(3)点P在y轴上,当三角形ABP的面积为6时,请直接写出点P的坐标.
21.如图,在直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求△ABC的面积;
(2)若把△ABC向下平移2个单位,再向右平移5个单位得到△A′B′C′,并写出C′的坐标.
22.如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式2=0
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,1),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在, 求出点P的坐标,若不存在,请说明理由.
23.在如图,所示的平面直角坐标系中描出下列各点:A(0,3),B(5,0),C(3,-5),D(-3,-5),E(3,5).
(1)点A到原点的距离是 ;
(2)将点C向x轴负方向平移6个单位长度后与点 重合;
(3)连接CE,则直线CE与y轴是什么位置关系
(4)点D到x轴,y轴的距离分别是多少
24.如图6,在平面直角坐标系中,三角形ABC的顶点都在格点上,其中,点C的坐标为(1,2).
(1)填空:点A的坐标是 ,点B的坐标是 ;
(2)将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度,得到三角形A'B'C',画出三角形A'B'C',并写出三角形A'B'C'三个顶点的坐标;
(3)求三角形ABC的面积.
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D B D C B D C C
二、填空题:
11.(-3,4)
12.(-1,1)或(7,1)
13.2,
14.【解答】解:∵A、B两点的坐标分别为(2,0)、(0,1),平移后A1(3,1),
∴线段AB向右平移1个单位,向上平移1个单位,
∴a=0+1=1,b=1+1=2,
点B1的坐标为(1,2),
故答案为:(1,2),
15、四
16、(-3,2)或(-3,-2)
17.【答案】5
【解析】由题中图象可知,.
18.【答案】
【解析】由题图可知,当时,,点;当时,,点;当时,,点.所以点的坐标为.
三.解答题:
19.(1)由题意可得:2m+1>0,m-3<0,解得:﹣<m<3;
(2)由题意可得:|2m+1|=3,解得:m=1或m=﹣2.
当m=1时,点P的坐标为(3,-2);
当m=﹣2时,点P的坐标为(﹣3,-5).
综上所述:点P的坐标为(3,﹣2)或(﹣3,-5).
20.解:(1)∵C(-1,-3),
∴|-3|=3,
∴点C到x轴的距离为3;
(2)∵A(-2,3)、B(4,3)、C(-1,-3)
∴AB=4-(-2) =6,点C到边AB的距离为:3-(-3) =6,
∴△ABC的面积为:6×6÷2=18.
(3)设点P的坐标为(0,y),
∵△ABP的面积为6,A(-2,3)、B(4,3),
∴×6×|x 3|=6,
∴|x-3|=2,
∴x=5或x=1,
∴P点的坐标为(0,5)或(0,1).
21.【分析】(1)根据三角形面积求法得出即可;
(2)根据已知将△ABC各顶点向下平移2个单位,向右平移5个单位得到各对应点,即可作图;进而得出点C′的坐标.
【解答】解:(1)△ABC的面积是:×3×5=7.5;
(2)作图如下:
∴点C′的坐标为:(1,1).
【点评】此题主要考查了平移变换以及三角形面积求法,正确平移图象的各顶点坐标是解题关键.
22.(1)a=2、b=3、c=4; (2)3 – m; (3)P(-3,1);
23..解:如图.
(1)3
(2)D
(3)直线CE与y轴平行.
(4)点D到x轴的距离是5,到y轴的距离是3.
24.解:(1)(2,-1) (4,3)
(2)如图,三角形A'B'C'即为所求作的图形;A'(0,0),B'(2,4),C'(-1,3).
(3)三角形ABC的面积为
3×4-×2×4-×3×1-×3×1=5.
www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
