二分法[下学期]
图片预览





文档简介
课件16张PPT。请你思考 从上海到美国旧金山的海底电缆有15个接点,现在某一接点发生故障,需及时修理,为了尽快断定故障发生点,一般至多需检查接点的个数为多少?一、 提出问题
能否求解下列方程能否解出上述方程的近似解?(精确到0.1)新教材研讨用二分法求方程的近似解
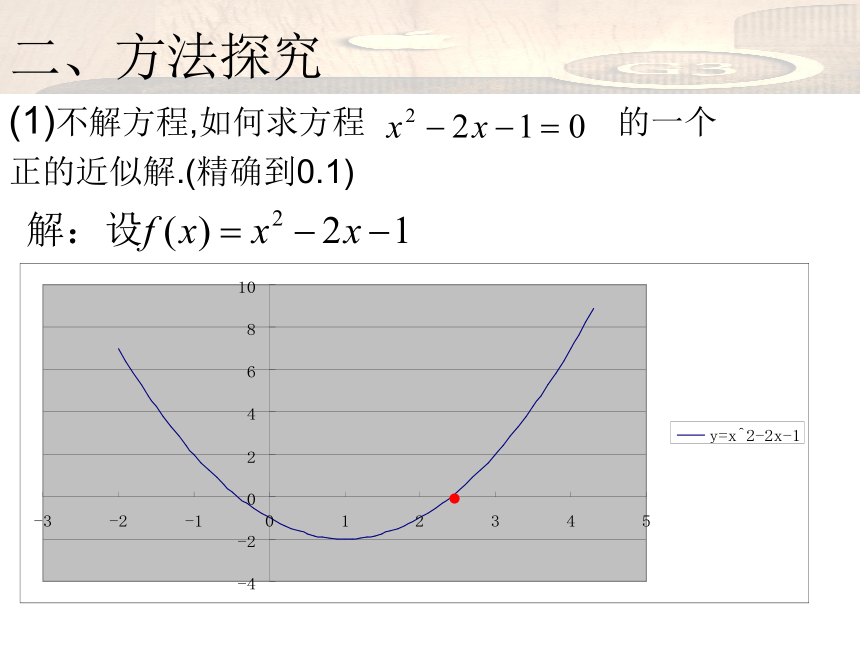
授课人:张丽二、方法探究(1)不解方程,如何求方程 的一个
正的近似解.(精确到0.1) f(2)<0, f(3)>0 2< <3
f(2)<0, f(2.5)>0 2< <2.5f(2.25)<0, f(2.5)>0 2.25< <2.5f(2.375)<0, f(2.5)>0 2.375< <2.5 f(2.375)<0,f(2.4375)>0 2.375< <2.4375二、方法探究 因为2.375及2.4375精确到0.1的近似值都为2.4 ,
所以原方程的近似解为x1≈ 2.4二、方法探究(2)能否简述上述求方程近似解的过程?
将方程的有根区间对分,然后再选择比原区间缩小一半的有根区间,如此继续下去,直到满足精度要求的根为止。(3)二分法(bisection method):
像上面这种求方程近似解的方法称为二分法,
它是求一元方程近似解的常用方法。运用二分法的
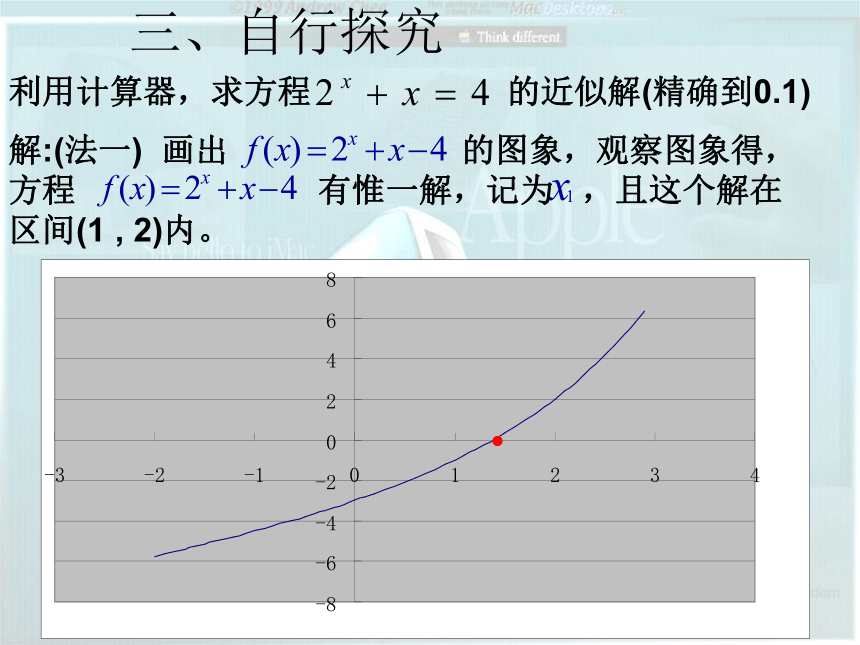
前提是要先判断某根所在的区间。三、自行探究利用计算器,求方程 的近似解(精确到0.1)
解:(法一) 画出 的图象,观察图象得,方程 有惟一解,记为 ,且这个解在区间(1 , 2)内。三、自行探究(1 , 2)f(1)<0,f(2)>01.5f(1.5)>0(1 , 1.5)f(1)<0, f(1.5)>01.25f(1.25)<0 (1.25 , 1.5)f(1.25)<0 , f(1.5)>01.375f(1.375)<0(1.375, 1.5)f(1.375)<0 , f(1.5)>01.4375f(1.4375)>0 (1.375,1.4375)f(1.375)<0 , f(1.4375)>0 因为1.375,1.4375精确到0.1的近似值都为1.4 ,所以原方程的近似解为x1≈ 1.4
三、自行探究 (法二)画出g(x)=2x及h(x)=4-x的图象,观察
图象得,方程2x+x=4有惟一解,记为x1,
且这个解在区间(1 , 2)内。四、归纳总结
用二分法求方程f(x)=0(或g(x)=h(x))近似解基本步骤:1、寻找解所在区间 (1)图象法 先画出y=f(x)图象,观察图象与x轴交点横坐标所处的范围;或画出y=g(x)和y=h(x)的图象,观察两图象的交点横坐标所处的范围。 把方程均转换为f(x)=0 的形式,再利用函数
y=f(x)的有关性质(如单调性),来判断解所在
的区间。(2)函数性态法四、归纳总结若x∈(a,b),不妨设f(a)<0,f(b)>0
3、根据精确度得出近似解
当x∈(m,n),且m,n根据精确度得到的近似值均为
同一个值p时,则x ≈ p,即求得了近似解。2、不断二分解所在的区间(3)若f( )=0,则x=(2) 若f( )<0,由f(b)>0,则x∈( ,b)对(1)、(2)两种情形再继续二分法所在的区间。五、知识拓展如何利用Excel来帮助研究方程的近似解?六、课堂练习课堂小结算法:如果一种计算方法对某一类问题(不是个别问题)都有效,计算可以一步一步地进行,每一步都能得到惟一的结果,我们常把这类问题的求解过程叫做解决这类问题的一种算法。
算法特点:算法是刻板的、机械的,有时要进行大量的重复计算,但它的优点是一种通法,只要按部就班地去做,总会算出结果。更大的优点是它可以让计算机来实现。
谢谢大家,
再见!
能否求解下列方程能否解出上述方程的近似解?(精确到0.1)新教材研讨用二分法求方程的近似解
授课人:张丽二、方法探究(1)不解方程,如何求方程 的一个
正的近似解.(精确到0.1) f(2)<0, f(3)>0 2< <3
f(2)<0, f(2.5)>0 2< <2.5f(2.25)<0, f(2.5)>0 2.25< <2.5f(2.375)<0, f(2.5)>0 2.375< <2.5 f(2.375)<0,f(2.4375)>0 2.375< <2.4375二、方法探究 因为2.375及2.4375精确到0.1的近似值都为2.4 ,
所以原方程的近似解为x1≈ 2.4二、方法探究(2)能否简述上述求方程近似解的过程?
将方程的有根区间对分,然后再选择比原区间缩小一半的有根区间,如此继续下去,直到满足精度要求的根为止。(3)二分法(bisection method):
像上面这种求方程近似解的方法称为二分法,
它是求一元方程近似解的常用方法。运用二分法的
前提是要先判断某根所在的区间。三、自行探究利用计算器,求方程 的近似解(精确到0.1)
解:(法一) 画出 的图象,观察图象得,方程 有惟一解,记为 ,且这个解在区间(1 , 2)内。三、自行探究(1 , 2)f(1)<0,f(2)>01.5f(1.5)>0(1 , 1.5)f(1)<0, f(1.5)>01.25f(1.25)<0 (1.25 , 1.5)f(1.25)<0 , f(1.5)>01.375f(1.375)<0(1.375, 1.5)f(1.375)<0 , f(1.5)>01.4375f(1.4375)>0 (1.375,1.4375)f(1.375)<0 , f(1.4375)>0 因为1.375,1.4375精确到0.1的近似值都为1.4 ,所以原方程的近似解为x1≈ 1.4
三、自行探究 (法二)画出g(x)=2x及h(x)=4-x的图象,观察
图象得,方程2x+x=4有惟一解,记为x1,
且这个解在区间(1 , 2)内。四、归纳总结
用二分法求方程f(x)=0(或g(x)=h(x))近似解基本步骤:1、寻找解所在区间 (1)图象法 先画出y=f(x)图象,观察图象与x轴交点横坐标所处的范围;或画出y=g(x)和y=h(x)的图象,观察两图象的交点横坐标所处的范围。 把方程均转换为f(x)=0 的形式,再利用函数
y=f(x)的有关性质(如单调性),来判断解所在
的区间。(2)函数性态法四、归纳总结若x∈(a,b),不妨设f(a)<0,f(b)>0
3、根据精确度得出近似解
当x∈(m,n),且m,n根据精确度得到的近似值均为
同一个值p时,则x ≈ p,即求得了近似解。2、不断二分解所在的区间(3)若f( )=0,则x=(2) 若f( )<0,由f(b)>0,则x∈( ,b)对(1)、(2)两种情形再继续二分法所在的区间。五、知识拓展如何利用Excel来帮助研究方程的近似解?六、课堂练习课堂小结算法:如果一种计算方法对某一类问题(不是个别问题)都有效,计算可以一步一步地进行,每一步都能得到惟一的结果,我们常把这类问题的求解过程叫做解决这类问题的一种算法。
算法特点:算法是刻板的、机械的,有时要进行大量的重复计算,但它的优点是一种通法,只要按部就班地去做,总会算出结果。更大的优点是它可以让计算机来实现。
谢谢大家,
再见!
