2022-2023小学数学人教版四年级下册第五单元达标测试(含答案)
文档属性
| 名称 | 2022-2023小学数学人教版四年级下册第五单元达标测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 329.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 11:36:01 | ||
图片预览

文档简介
第五单元巩固练习
一、填空。(第1题4分,第2题3分,其余每空2分,共29分)
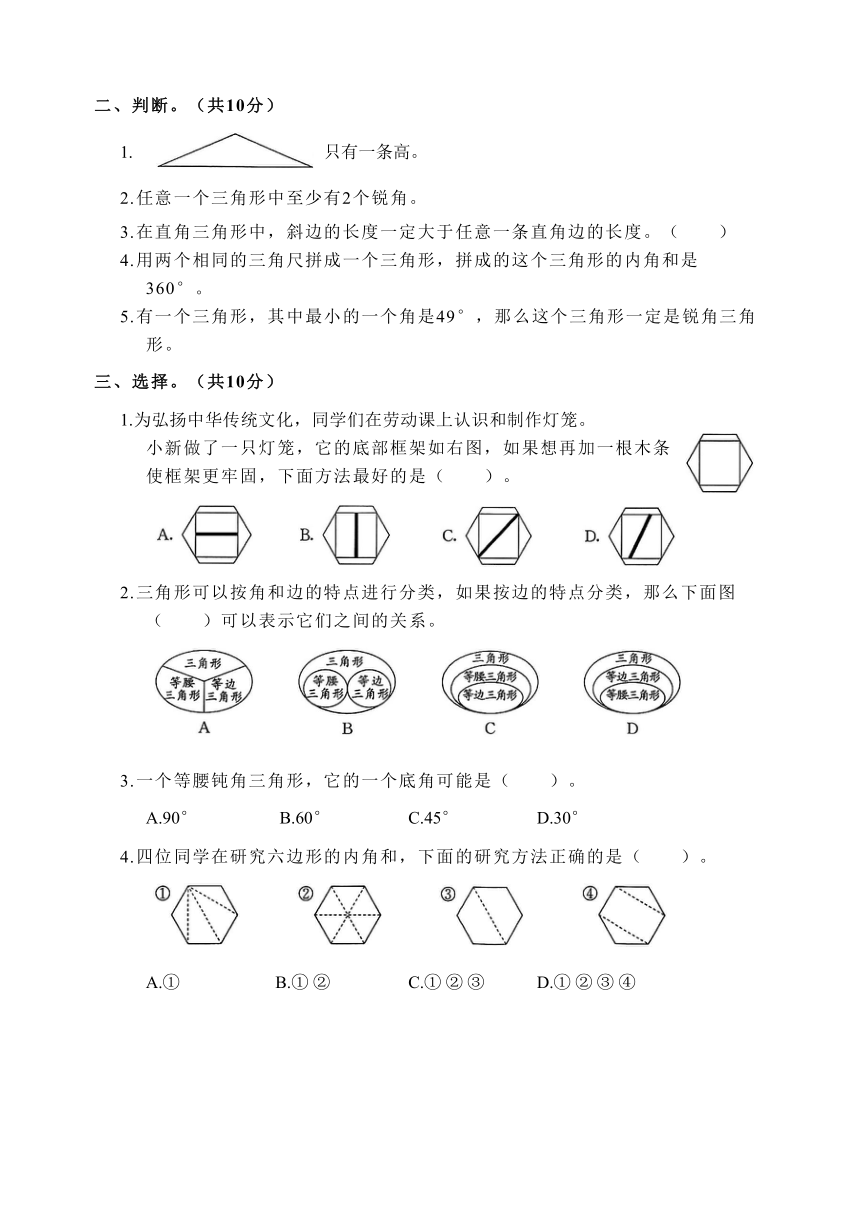
1.如图,三角形ABC是( )三角形,BC边对应的高是线段( ),线段BD是( )边对应的高。已知∠1=52°,那么∠2=( )°。
2.丁楠去外婆家走( )号路最近,理由是( )。
3.在三角形ABC中,已知∠A=72°,∠B=48°,则∠C=( )°,这是一个( )三角形。(按角分类)
4.一个等边三角形,周长是15cm,每条边的长度是( )cm,它的每个内角是( )°。
已知三角形中的一个内角是20°,剪去这个角后(如右图),剩下的图形的内角和是( )°。
6.如果一个三角形的两条边分别是7cm和14cm,那么它的第三条边最长是( )cm,最短是( )cm。(长度取整厘米数)
7.一根铁丝正好围成一个边长为6cm的等边三角形,如果把它改围成一条边为4cm的等腰三角形,那么另外两条边为( )cm和( )cm。
8.把一张长方形纸沿对角线折叠(如右图),经过计算得出∠1= ( )°。
9.数一数,右面的图形一共有( )个三角形。
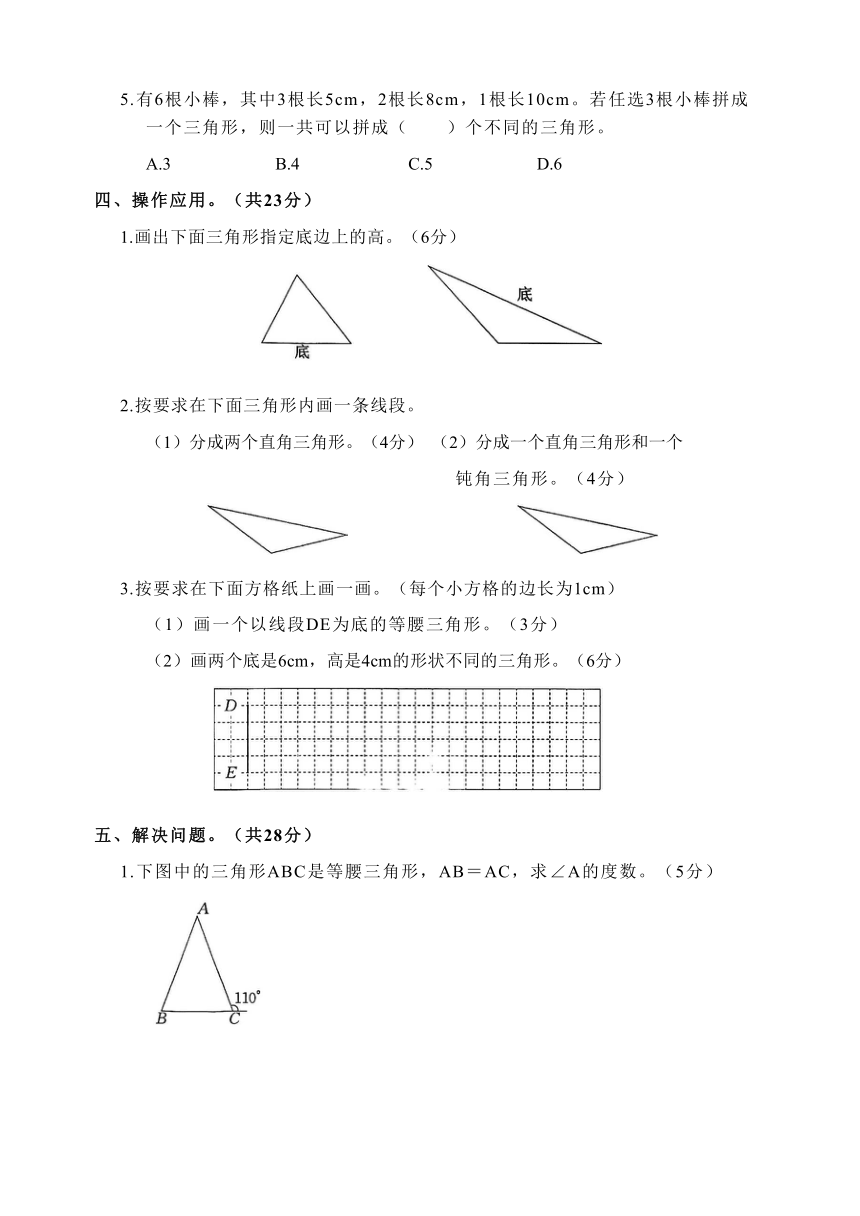
二、判断。(共10分)
1. 只有一条高。
2.任意一个三角形中至少有2个锐角。
3.在直角三角形中,斜边的长度一定大于任意一条直角边的长度。( )
4.用两个相同的三角尺拼成一个三角形,拼成的这个三角形的内角和是360°。
5.有一个三角形,其中最小的一个角是49°,那么这个三角形一定是锐角三角形。
三、选择。(共10分)
1.为弘扬中华传统文化,同学们在劳动课上认识和制作灯笼。
小新做了一只灯笼,它的底部框架如右图,如果想再加一根木条使框架更牢固,下面方法最好的是( )。
2.三角形可以按角和边的特点进行分类,如果按边的特点分类,那么下面图( )可以表示它们之间的关系。
3.一个等腰钝角三角形,它的一个底角可能是( )。
A.90° B.60° C.45° D.30°
4.四位同学在研究六边形的内角和,下面的研究方法正确的是( )。
A.① B.① ② C.① ② ③ D.① ② ③ ④
5.有6根小棒,其中3根长5cm,2根长8cm,1根长10cm。若任选3根小棒拼成一个三角形,则一共可以拼成( )个不同的三角形。
A.3 B.4 C.5 D.6
四、操作应用。(共23分)
1.画出下面三角形指定底边上的高。(6分)
2.按要求在下面三角形内画一条线段。
(1)分成两个直角三角形。(4分) (2)分成一个直角三角形和一个
钝角三角形。(4分)
3.按要求在下面方格纸上画一画。(每个小方格的边长为1cm)
(1)画一个以线段DE为底的等腰三角形。(3分)
(2)画两个底是6cm,高是4cm的形状不同的三角形。(6分)
五、解决问题。(共28分)
1.下图中的三角形ABC是等腰三角形,AB=AC,求∠A的度数。(5分)
2.一个等腰三角形的两条边分别为3cm和5cm,那么这个三角形的周长是多少厘米?(5分)
3.聪聪想把11cm长的铁丝剪成三段围成一个三角形(长度取整厘米数),剪成的三段分别长多少?至少写出2种情况并说明理由。(6分)
4.如图,如果∠1=∠B,那么∠2一定等于∠C。请有理有据地说明∠2=∠C。(6分)
5.一个三角形中,最大角的度数是最小角的3倍,第三个角的度数是最小角的2倍,你知道这个三角形三个角的度数吗?这是一个什么三角形?(6分)
答案:
一、1.直角 AB AC 38
② 两点间所有连线中线段最短
3.60 锐角 4.5 60 5.360
6.20 8 7.7 7 8.25 9.30
二、1.× 2.√ 3.√ 4.× 5.√
三、1.C 2.C 3.D 4.D 5.C
四、1.
2.(1)
(2)
(画法不唯一)
示例:(1)(2)如图
五、1.180°-110°=70° 180°-70°×2=40°
答:∠A的度数是40°。
2.3+3=6(cm)
6>5,满足三角形的三边关系。
3+3+5=11(cm)
3+5=8(cm)
8>5,满足三角形的三边关系。
5+5+3=13(cm)
答:这个三角形的周长是11cm或13cm。
3.示例:剪成的三段分别长1cm、5cm、 5cm或2cm、4cm、5cm。
理由:三角形任意两边的和大于第三边。
4.因为∠A+∠1+∠2=180° ∠A+∠B+∠C=180°所以∠2=180°-∠A-∠1 ∠C=180°-∠A-∠B
又因为∠1=∠B所以∠2=∠C
5.(线段图略)
180°÷(3+2+1)=30°
30°×2=60° 30°×3=90°
答:这个三角形三个角的度数分别是30°、60°和90°,这是一个直角三角形。
一、填空。(第1题4分,第2题3分,其余每空2分,共29分)
1.如图,三角形ABC是( )三角形,BC边对应的高是线段( ),线段BD是( )边对应的高。已知∠1=52°,那么∠2=( )°。
2.丁楠去外婆家走( )号路最近,理由是( )。
3.在三角形ABC中,已知∠A=72°,∠B=48°,则∠C=( )°,这是一个( )三角形。(按角分类)
4.一个等边三角形,周长是15cm,每条边的长度是( )cm,它的每个内角是( )°。
已知三角形中的一个内角是20°,剪去这个角后(如右图),剩下的图形的内角和是( )°。
6.如果一个三角形的两条边分别是7cm和14cm,那么它的第三条边最长是( )cm,最短是( )cm。(长度取整厘米数)
7.一根铁丝正好围成一个边长为6cm的等边三角形,如果把它改围成一条边为4cm的等腰三角形,那么另外两条边为( )cm和( )cm。
8.把一张长方形纸沿对角线折叠(如右图),经过计算得出∠1= ( )°。
9.数一数,右面的图形一共有( )个三角形。
二、判断。(共10分)
1. 只有一条高。
2.任意一个三角形中至少有2个锐角。
3.在直角三角形中,斜边的长度一定大于任意一条直角边的长度。( )
4.用两个相同的三角尺拼成一个三角形,拼成的这个三角形的内角和是360°。
5.有一个三角形,其中最小的一个角是49°,那么这个三角形一定是锐角三角形。
三、选择。(共10分)
1.为弘扬中华传统文化,同学们在劳动课上认识和制作灯笼。
小新做了一只灯笼,它的底部框架如右图,如果想再加一根木条使框架更牢固,下面方法最好的是( )。
2.三角形可以按角和边的特点进行分类,如果按边的特点分类,那么下面图( )可以表示它们之间的关系。
3.一个等腰钝角三角形,它的一个底角可能是( )。
A.90° B.60° C.45° D.30°
4.四位同学在研究六边形的内角和,下面的研究方法正确的是( )。
A.① B.① ② C.① ② ③ D.① ② ③ ④
5.有6根小棒,其中3根长5cm,2根长8cm,1根长10cm。若任选3根小棒拼成一个三角形,则一共可以拼成( )个不同的三角形。
A.3 B.4 C.5 D.6
四、操作应用。(共23分)
1.画出下面三角形指定底边上的高。(6分)
2.按要求在下面三角形内画一条线段。
(1)分成两个直角三角形。(4分) (2)分成一个直角三角形和一个
钝角三角形。(4分)
3.按要求在下面方格纸上画一画。(每个小方格的边长为1cm)
(1)画一个以线段DE为底的等腰三角形。(3分)
(2)画两个底是6cm,高是4cm的形状不同的三角形。(6分)
五、解决问题。(共28分)
1.下图中的三角形ABC是等腰三角形,AB=AC,求∠A的度数。(5分)
2.一个等腰三角形的两条边分别为3cm和5cm,那么这个三角形的周长是多少厘米?(5分)
3.聪聪想把11cm长的铁丝剪成三段围成一个三角形(长度取整厘米数),剪成的三段分别长多少?至少写出2种情况并说明理由。(6分)
4.如图,如果∠1=∠B,那么∠2一定等于∠C。请有理有据地说明∠2=∠C。(6分)
5.一个三角形中,最大角的度数是最小角的3倍,第三个角的度数是最小角的2倍,你知道这个三角形三个角的度数吗?这是一个什么三角形?(6分)
答案:
一、1.直角 AB AC 38
② 两点间所有连线中线段最短
3.60 锐角 4.5 60 5.360
6.20 8 7.7 7 8.25 9.30
二、1.× 2.√ 3.√ 4.× 5.√
三、1.C 2.C 3.D 4.D 5.C
四、1.
2.(1)
(2)
(画法不唯一)
示例:(1)(2)如图
五、1.180°-110°=70° 180°-70°×2=40°
答:∠A的度数是40°。
2.3+3=6(cm)
6>5,满足三角形的三边关系。
3+3+5=11(cm)
3+5=8(cm)
8>5,满足三角形的三边关系。
5+5+3=13(cm)
答:这个三角形的周长是11cm或13cm。
3.示例:剪成的三段分别长1cm、5cm、 5cm或2cm、4cm、5cm。
理由:三角形任意两边的和大于第三边。
4.因为∠A+∠1+∠2=180° ∠A+∠B+∠C=180°所以∠2=180°-∠A-∠1 ∠C=180°-∠A-∠B
又因为∠1=∠B所以∠2=∠C
5.(线段图略)
180°÷(3+2+1)=30°
30°×2=60° 30°×3=90°
答:这个三角形三个角的度数分别是30°、60°和90°,这是一个直角三角形。
