12.2三角形全等的判定2 课件
文档属性
| 名称 | 12.2三角形全等的判定2 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 754.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-12 21:03:01 | ||
图片预览




文档简介
课件28张PPT。§12.2 三角形全等的判定 (第2课时)1.理解判定三角形全等的“边角边”条件.
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
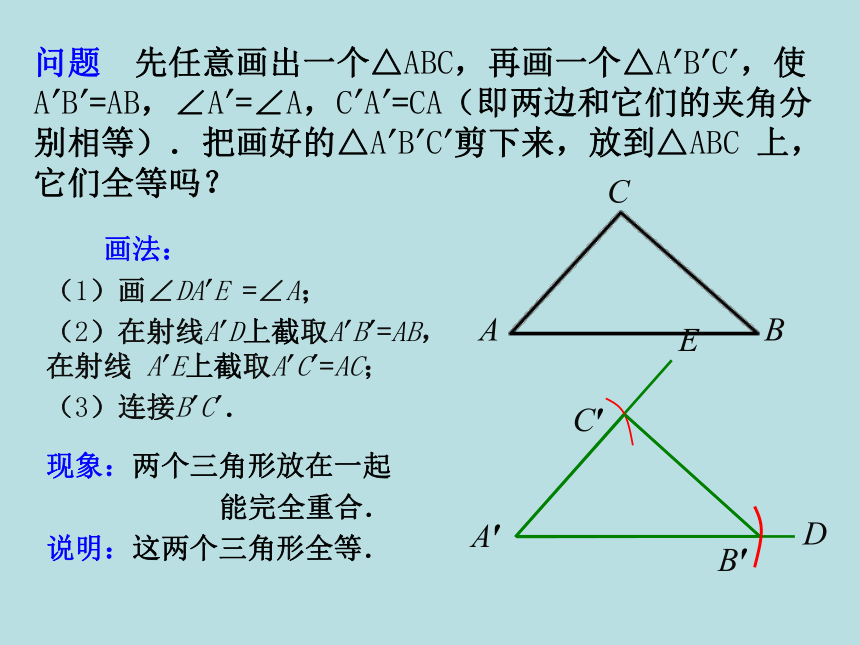
3.能运用“SAS”证明简单的三角形全等问题.三边对应相等的两个三角形全等
(可以简写为“边边边”或“SSS”).在△ABC和△ DEF中∴ △ABC ≌△ DEF(SSS)用符号语言表达为: 三角形全等判定方法1忆一忆除了SSS外,还有其他情况吗?继续探索三角形全等的条件.当两个三角形满足六个条件中的三个时,有四种情况:SSS不能?1.三个角.
2.三条边.
3.两边一角.
4.两角一边.现象:两个三角形放在一起
能完全重合.
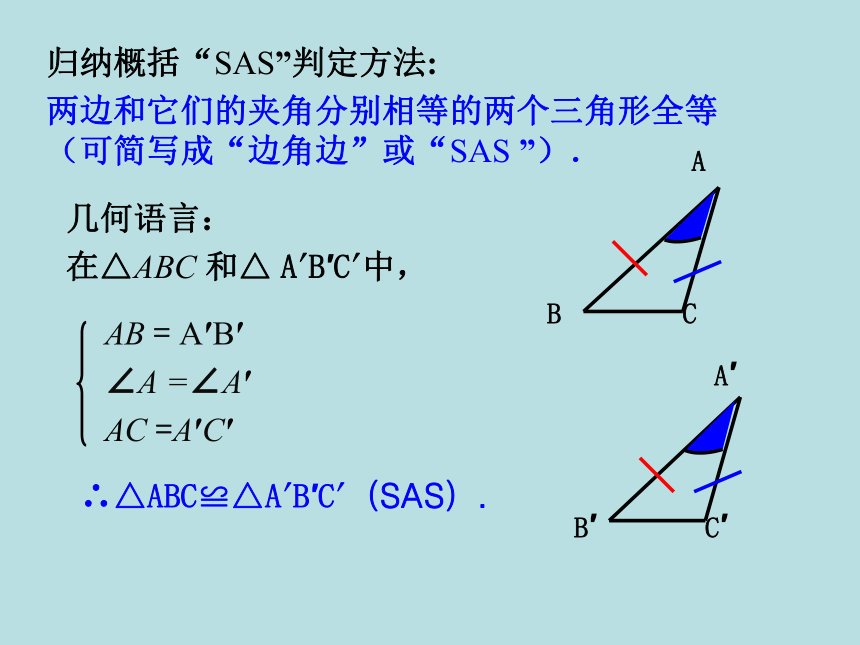
说明:这两个三角形全等. 画法:
(1)画∠DA′E =∠A;
(2)在射线A′D上截取A′B′=AB,在射线 A′E上截取A′C′=AC;
(3)连接B′C′.问题 先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,∠A′=∠A,C′A′=CA(即两边和它们的夹角分别相等).把画好的△A′B′C′剪下来,放到△ABC 上,它们全等吗?几何语言:
在△ABC 和△ A′B′C′中,归纳概括“SAS”判定方法:
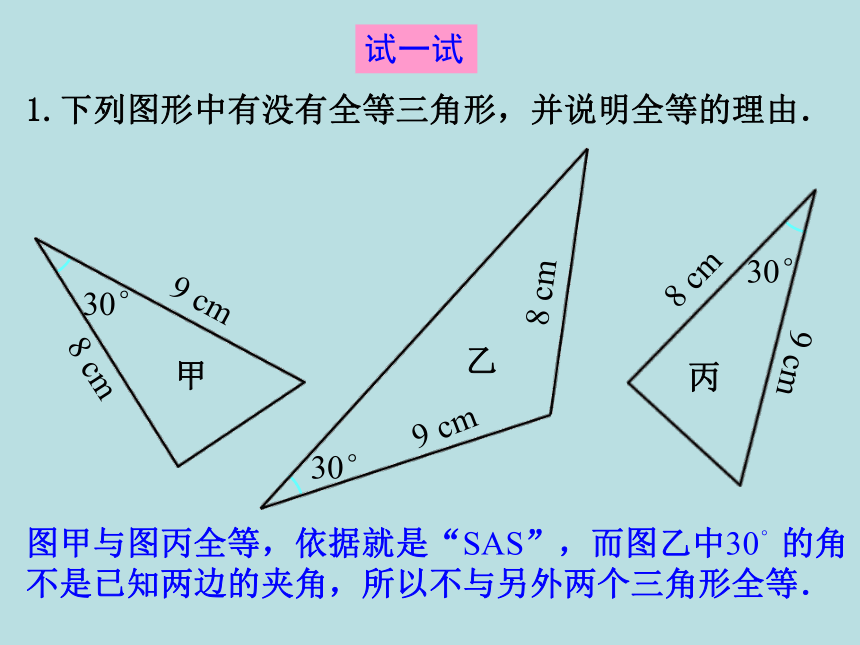
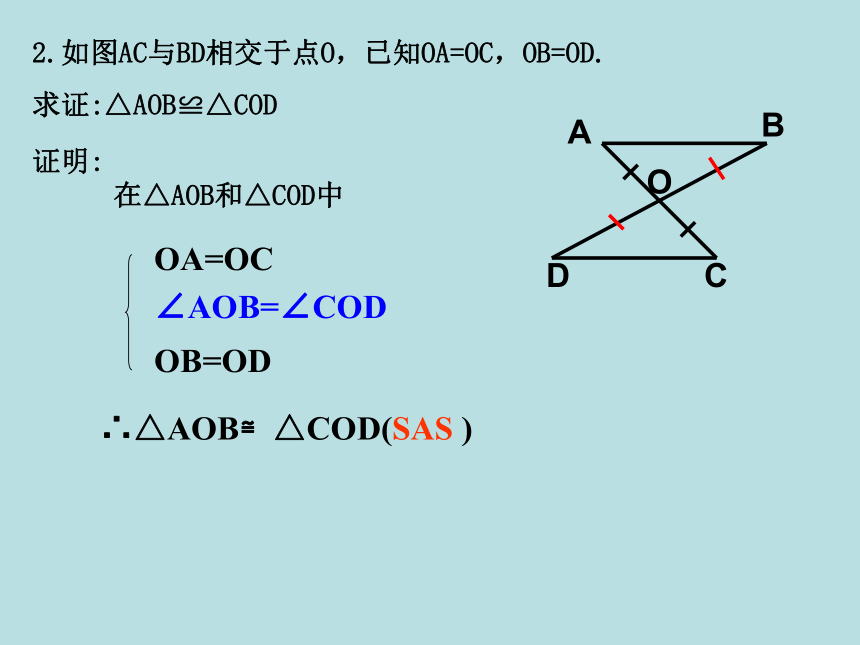
两边和它们的夹角分别相等的两个三角形全等(可简写成“边角边”或“SAS ”).∴△ABC≌△A′B′C′(SAS). 1.下列图形中有没有全等三角形,并说明全等的理由.图甲与图丙全等,依据就是“SAS”,而图乙中30°的角不是已知两边的夹角,所以不与另外两个三角形全等.试一试2.如图AC与BD相交于点O,已知OA=OC,OB=OD.
求证:△AOB≌△COD证明:在△AOB和△COD中OA=OCOB=OD∠AOB=∠COD∴△AOB≌△COD(SAS ) 利用今天所学“边角边”知识,带黑色的那块.因为它完整地保留了两边及其夹角,一个三角形两条边的长度和夹角的大小确定了,这个三角形的形状、大小就确定下来了.某同学不小心把一块三角形的玻璃从两个顶点处打碎成两块(如图),现要到玻璃店去配一块完全一样的玻璃.请问如果只准带一块碎片,应该带哪一
块去,能试着说明理由吗?证明:在△ABC 和△DEC 中,∴ △ABC ≌△DEC(SAS).
∴ AB =DE
(全等三角形的对应边相等).例1 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个不经过池塘可以直接到达点A 和B的点C,连接AC并延长至D,使CD =CA,连接BC 并延长至E,使CE =CB,连接ED,那么量出DE的长就是A,B的距离.为什么?证明:在△ABC与△BAD中AC=BD
∠CAB=∠DBA
AB=BA∴△ABC≌△BAD(SAS)(已知)(已知)(公共边)∴BC=AD (全等三角形的对应边相等)可以看出,因为全等三角形的对应边相等,对应角相等,所以证明分别属于两个三角形的线段相等或者角相等的问题,常通过证明这两个三角形全等来解决。例2. 如图,AC=BD,∠CAB= ∠DBA,你能判断BC=AD吗?ADCB做一做1、如图,两车从路段AB的一端A出发,分别向东,向西行进相同的距离,到达C、D两地,此时C、D到B的距离相等吗?为什么?证明:在△ABC与△ABD中AB=AB(公共边)∠ BAC= ∠ BAD=90°AC=AD(已知)∴△ABC≌△ABD(SAS)∴BC=BD (全等三角形的对应边相等)ADCBFE做一做2、如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.
求证:∠A=∠D如图,在△ABC 和△ABD 中.
AB =AB,AC = AD,∠B =∠B,
但△ABC 和△ABD 不全等. 两边一角分别相等包括“两边夹角”和 “两边及其中一边的对角”分别相等两种情况,前面已探索出“SAS”判定三角形全等的方法,那么由“SSA” 的条件能判定两个三角形全等吗?把一长一短的两根细木棍的一端用螺钉铰合在一起,使长木棍的另一端与射线BC的端点B重合,适当调整好长木棍与射线BC所成的角后,固定住长木棍,把短木棍摆起来.有两边及其中一边的对角分别相等的两个三角形不一定全等。ABDABCSSA不能判定全等C1.在下列推理中填写需要补充
的条件,使结论成立:
(1)如图,在△AOB和△DOC中AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC( )∠ AOB∠ DOC对顶角相等SAS做一做(2)如图,在△AEC和△ADB中,已知AE=AD,AC=AB,请说明△AEC ≌ △ADB的理由。____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB( )AEADACABSAS解:在△AEC和△ADB中三角形全等判定方法2用符号语言表达为:在△ABC与△DEF中∴△ABC≌△DEF(SAS)两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)FEDCBA小结1.若AB=AC,则添加什么条件可得△ABD≌ △ACD?△ABD≌ △ACDAB=AC∠BAD= ∠CADSA SAD=ADBD=CDS2.如图,要证△ACB≌ △ADB ,至少选用哪些条件可证得△ACB≌ △ADB。ABCD△ACB≌ △ADBSASAB=AB∠CAB= ∠ DABAC=ADSBC=BD3.如图,已知AB=DE,AC=DF,要说明△ABC≌△DEF,还需增加一个什么条件?●●●●4.如图:己知AD∥BC,AE=CF,AD=BC,E、F都在直线AC上,试说明DE∥BF。1.已知:如图,AB=CB,∠1=∠2。△ABD 和△CBD 全等吗?ABCD12变式1:已知:如图,AB=CB,∠1= ∠2
求证:(1) AD=CD (2)BD 平分∠ ADCABCD变式2:
已知:AD=CD,BD平分∠ADC
求证:∠A=∠C12证明两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等而得到。2.如图,AC=BD,∠1= ∠2
求证:BC=AD变式1: 如图,AC=BD,BC=AD
求证:∠1= ∠2变式2: 如图,AC=BD,BC=AD
求证:∠C=∠D变式3: 如图,AC=BD,BC=AD
求证:∠A=∠BAC=DF(已知),
∠A=∠D (已证),
AB=DE (已证),
∴△EFD≌△BCA(SAS),证明:
∵AC∥DF,
∴∠A=∠D(两直线平行,内错角相等)
又∵ AE=DB,
∴ AE+BE=DB+BE,即AB=DE.
在△EFD和△BCA中,∴ ∠ABC=∠DEF(全等三角形的对应角相等)
∴EF‖BC(内错角相等,两直线平行)3.如图,点A,E,B,D在同一条直线上,AE=DB,AC=DF,AC∥DF.请探索BC与EF有怎样的位置关系?好好学习天天向上
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3.能运用“SAS”证明简单的三角形全等问题.三边对应相等的两个三角形全等
(可以简写为“边边边”或“SSS”).在△ABC和△ DEF中∴ △ABC ≌△ DEF(SSS)用符号语言表达为: 三角形全等判定方法1忆一忆除了SSS外,还有其他情况吗?继续探索三角形全等的条件.当两个三角形满足六个条件中的三个时,有四种情况:SSS不能?1.三个角.
2.三条边.
3.两边一角.
4.两角一边.现象:两个三角形放在一起
能完全重合.
说明:这两个三角形全等. 画法:
(1)画∠DA′E =∠A;
(2)在射线A′D上截取A′B′=AB,在射线 A′E上截取A′C′=AC;
(3)连接B′C′.问题 先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,∠A′=∠A,C′A′=CA(即两边和它们的夹角分别相等).把画好的△A′B′C′剪下来,放到△ABC 上,它们全等吗?几何语言:
在△ABC 和△ A′B′C′中,归纳概括“SAS”判定方法:
两边和它们的夹角分别相等的两个三角形全等(可简写成“边角边”或“SAS ”).∴△ABC≌△A′B′C′(SAS). 1.下列图形中有没有全等三角形,并说明全等的理由.图甲与图丙全等,依据就是“SAS”,而图乙中30°的角不是已知两边的夹角,所以不与另外两个三角形全等.试一试2.如图AC与BD相交于点O,已知OA=OC,OB=OD.
求证:△AOB≌△COD证明:在△AOB和△COD中OA=OCOB=OD∠AOB=∠COD∴△AOB≌△COD(SAS ) 利用今天所学“边角边”知识,带黑色的那块.因为它完整地保留了两边及其夹角,一个三角形两条边的长度和夹角的大小确定了,这个三角形的形状、大小就确定下来了.某同学不小心把一块三角形的玻璃从两个顶点处打碎成两块(如图),现要到玻璃店去配一块完全一样的玻璃.请问如果只准带一块碎片,应该带哪一
块去,能试着说明理由吗?证明:在△ABC 和△DEC 中,∴ △ABC ≌△DEC(SAS).
∴ AB =DE
(全等三角形的对应边相等).例1 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个不经过池塘可以直接到达点A 和B的点C,连接AC并延长至D,使CD =CA,连接BC 并延长至E,使CE =CB,连接ED,那么量出DE的长就是A,B的距离.为什么?证明:在△ABC与△BAD中AC=BD
∠CAB=∠DBA
AB=BA∴△ABC≌△BAD(SAS)(已知)(已知)(公共边)∴BC=AD (全等三角形的对应边相等)可以看出,因为全等三角形的对应边相等,对应角相等,所以证明分别属于两个三角形的线段相等或者角相等的问题,常通过证明这两个三角形全等来解决。例2. 如图,AC=BD,∠CAB= ∠DBA,你能判断BC=AD吗?ADCB做一做1、如图,两车从路段AB的一端A出发,分别向东,向西行进相同的距离,到达C、D两地,此时C、D到B的距离相等吗?为什么?证明:在△ABC与△ABD中AB=AB(公共边)∠ BAC= ∠ BAD=90°AC=AD(已知)∴△ABC≌△ABD(SAS)∴BC=BD (全等三角形的对应边相等)ADCBFE做一做2、如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.
求证:∠A=∠D如图,在△ABC 和△ABD 中.
AB =AB,AC = AD,∠B =∠B,
但△ABC 和△ABD 不全等. 两边一角分别相等包括“两边夹角”和 “两边及其中一边的对角”分别相等两种情况,前面已探索出“SAS”判定三角形全等的方法,那么由“SSA” 的条件能判定两个三角形全等吗?把一长一短的两根细木棍的一端用螺钉铰合在一起,使长木棍的另一端与射线BC的端点B重合,适当调整好长木棍与射线BC所成的角后,固定住长木棍,把短木棍摆起来.有两边及其中一边的对角分别相等的两个三角形不一定全等。ABDABCSSA不能判定全等C1.在下列推理中填写需要补充
的条件,使结论成立:
(1)如图,在△AOB和△DOC中AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC( )∠ AOB∠ DOC对顶角相等SAS做一做(2)如图,在△AEC和△ADB中,已知AE=AD,AC=AB,请说明△AEC ≌ △ADB的理由。____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB( )AEADACABSAS解:在△AEC和△ADB中三角形全等判定方法2用符号语言表达为:在△ABC与△DEF中∴△ABC≌△DEF(SAS)两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)FEDCBA小结1.若AB=AC,则添加什么条件可得△ABD≌ △ACD?△ABD≌ △ACDAB=AC∠BAD= ∠CADSA SAD=ADBD=CDS2.如图,要证△ACB≌ △ADB ,至少选用哪些条件可证得△ACB≌ △ADB。ABCD△ACB≌ △ADBSASAB=AB∠CAB= ∠ DABAC=ADSBC=BD3.如图,已知AB=DE,AC=DF,要说明△ABC≌△DEF,还需增加一个什么条件?●●●●4.如图:己知AD∥BC,AE=CF,AD=BC,E、F都在直线AC上,试说明DE∥BF。1.已知:如图,AB=CB,∠1=∠2。△ABD 和△CBD 全等吗?ABCD12变式1:已知:如图,AB=CB,∠1= ∠2
求证:(1) AD=CD (2)BD 平分∠ ADCABCD变式2:
已知:AD=CD,BD平分∠ADC
求证:∠A=∠C12证明两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等而得到。2.如图,AC=BD,∠1= ∠2
求证:BC=AD变式1: 如图,AC=BD,BC=AD
求证:∠1= ∠2变式2: 如图,AC=BD,BC=AD
求证:∠C=∠D变式3: 如图,AC=BD,BC=AD
求证:∠A=∠BAC=DF(已知),
∠A=∠D (已证),
AB=DE (已证),
∴△EFD≌△BCA(SAS),证明:
∵AC∥DF,
∴∠A=∠D(两直线平行,内错角相等)
又∵ AE=DB,
∴ AE+BE=DB+BE,即AB=DE.
在△EFD和△BCA中,∴ ∠ABC=∠DEF(全等三角形的对应角相等)
∴EF‖BC(内错角相等,两直线平行)3.如图,点A,E,B,D在同一条直线上,AE=DB,AC=DF,AC∥DF.请探索BC与EF有怎样的位置关系?好好学习天天向上
