12.2三角形全等的判定3 课件
文档属性
| 名称 | 12.2三角形全等的判定3 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 768.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-12 21:04:52 | ||
图片预览



文档简介
课件23张PPT。§12.2 三角形全等的判定 (第3课时)1.探索并正确理解“ASA”和“AAS”判定方法.
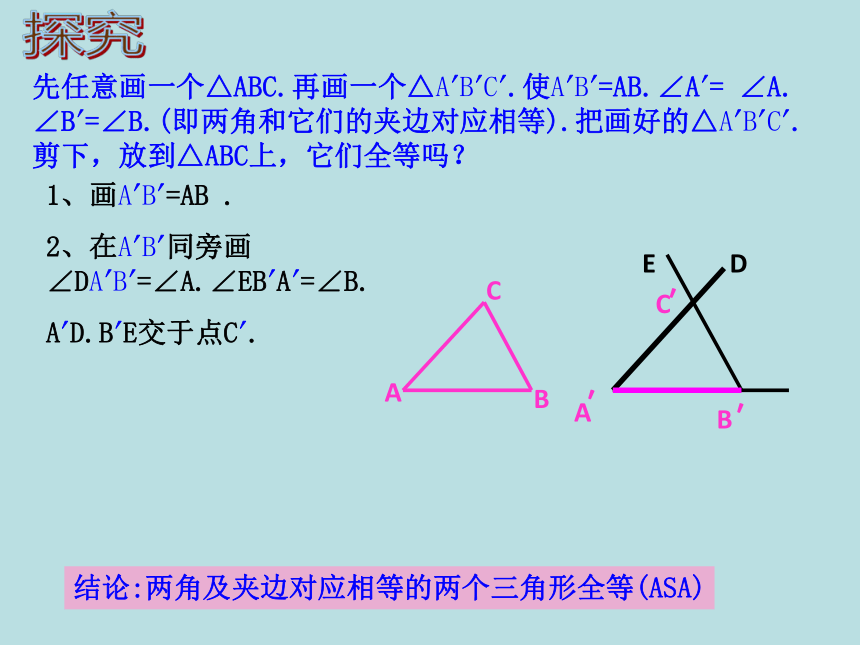
2.会用“ASA”和“AAS”判定方法证明两个三角形全等. 1.什么是全等三角形?2.我们已经学过了哪几种判定两个三角形全等的方法?能够完全重合的两个三角形叫做全等三角形.边边边(SSS)和边角边(SAS)结论:两角及夹边对应相等的两个三角形全等(ASA)A′EDCB′′先任意画一个△ABC.再画一个△A′B′C′.使A′B′=AB.∠A′= ∠A.
∠B′=∠B.(即两角和它们的夹边对应相等).把画好的△A′B′C′.剪下,放到△ABC上,它们全等吗?1、画A′B′=AB .
2、在A′B′同旁画∠DA′B′=∠A.∠EB′A′=∠B.
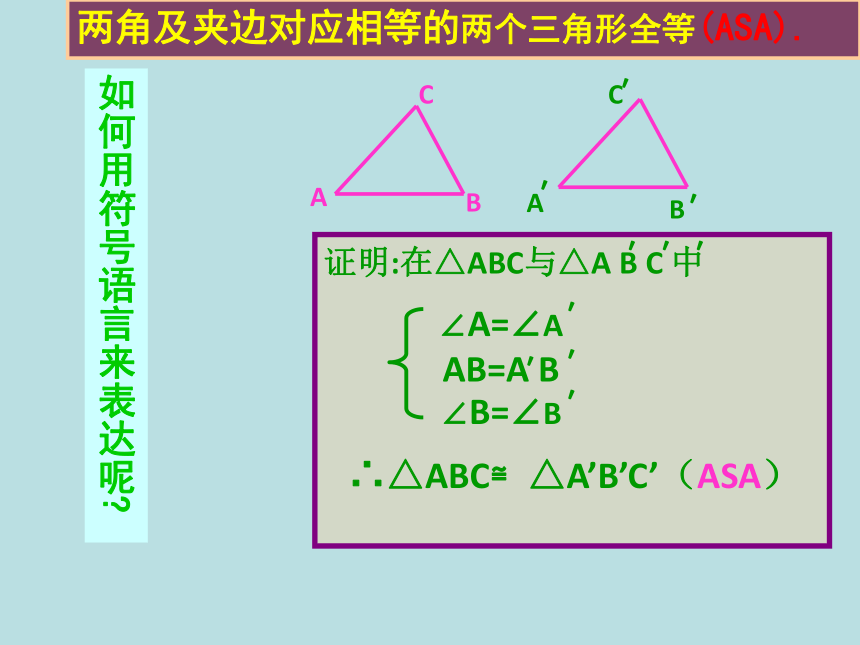
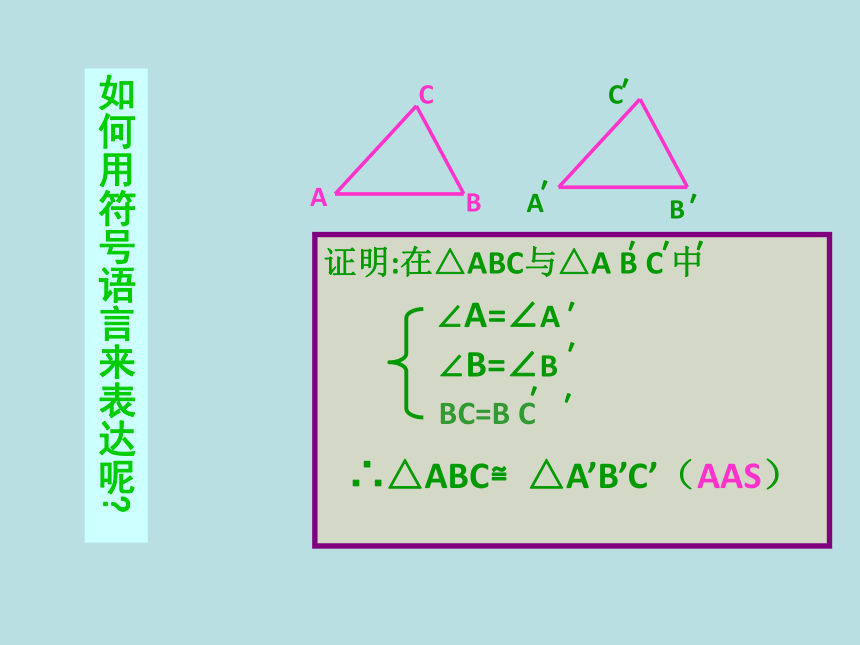
A′D.B′E交于点C′.探究如何用符号语言来表达呢?证明:在△ABC与△A B C 中∠A=∠A AB=A B∴△ABC≌△A’B’C’(ASA)ACB′′′′′′∠B=∠B′两角及夹边对应相等的两个三角形全等(ASA).证明:在△ABE 和△ACD 中,∴△ABE ≌△ACD(ASA).
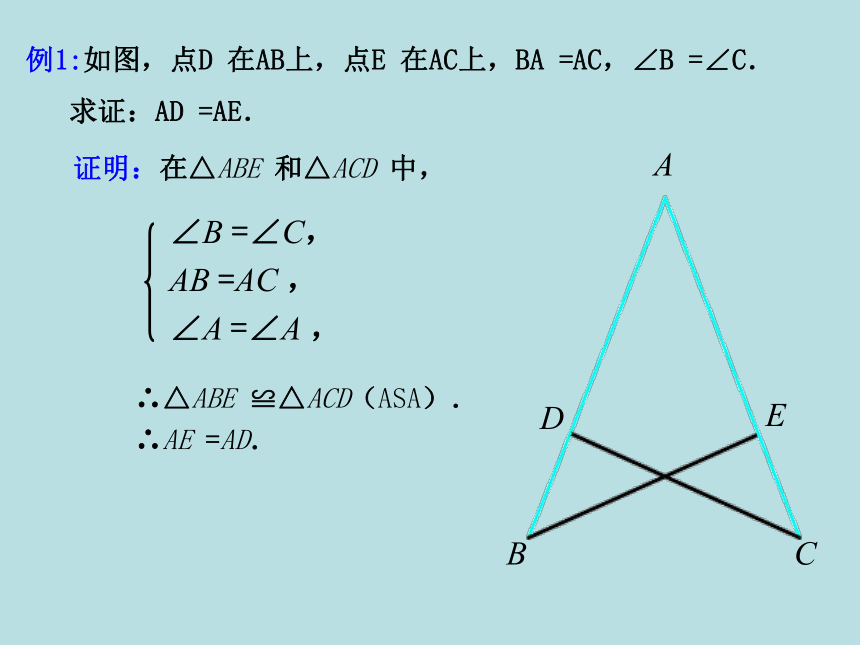
∴AE =AD. 例1:如图,点D 在AB上,点E 在AC上,BA =AC,∠B =∠C.
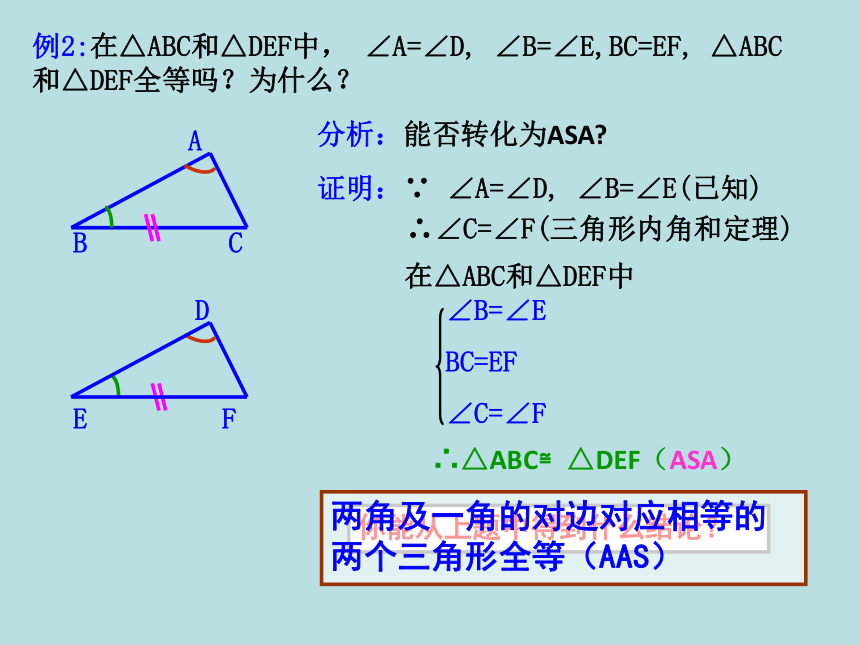
求证:AD =AE. ACBEDF分析:能否转化为ASA?证明:∵ ∠A=∠D, ∠B=∠E(已知) ∴∠C=∠F(三角形内角和定理)∠B=∠E
BC=EF
∠C=∠F在△ABC和△DEF中∴△ABC≌△DEF(ASA)你能从上题中得到什么结论?两角及一角的对边对应相等的两个三角形全等(AAS)例2:在△ABC和△DEF中, ∠A=∠D, ∠B=∠E,BC=EF, △ABC和△DEF全等吗?为什么?如何用符号语言来表达呢?证明:在△ABC与△A B C 中∠A=∠A∴△ABC≌△A’B’C’(AAS)ACB′′′′∠B=∠B′问题3 如图,小明、小强一起踢球,不小心把一块三角形的装饰玻璃踢碎了,摔成了3 块,两人决定赔偿.你能告诉他们只带其中哪一块去玻璃店,就可以买到一块完全一样的玻璃吗?1、如图,要测量河两岸相对两点A,B两点的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得DE的长就是AB的长,为什么?12ABCD2、如图,AB⊥BC, AD⊥DC ,∠1= ∠2,
求证:AB=AD在△ABD和△ABC中
∠1=∠2 (已知)
∠C=∠D (已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)1.已知,如图,∠1=∠2,∠C=∠D,求证:AC=AD12【证明】证明:∵ ∠DAB =∠EAC,
∴ ∠DAC =∠EAB.
∵ AE⊥BE,AD⊥DC,
∴ ∠D =∠E =90°.
在△ADC 和△AEB 中, 例2 如图,AE⊥BE,AD⊥DC,CD =BE,∠DAB
=∠EAC.求证:AB =AC. ∴ △ADC ≌△AEB(AAS).
∴ AC =AB. 例2 如图,AE⊥BE,AD⊥DC,CD =BE,∠DAB
=∠EAC.求证:AB =AC. 证明:例1 、如图 ,AB=AC,∠B=∠C,那么△ABE和△ACD全等吗?为什么?证明: 在△ABE与△ACD中
∠B=∠C (已知)
AB=AC (已知)
∠A= ∠A (公共角)
∴ △ABE ≌△ACD (ASA) 1.如图,AD=AE,∠B=∠C,那么BE和CD相等么?为什么?变一变BE=CD你还能得出其他
什么结论?O 练习 如图,E,F 在线段AC上,AD∥CB,AE =
CF.若∠B =∠D,求证:DF =BE.证明:∵ AD∥CB ,
∴ ∠A =∠C.
∵ AE =CF ,
∴ AF =CE.
在△ADF 和△CBE 中, 练习 如图,E,F 在线段AC上,AD∥CB,AE =
CF.若∠B =∠D,求证:DF =BE.∴ △ADF ≌△CBE(AAS).
∴ DF =BE.证明: 变式 若将条件 “∠B =∠D”变为“DF∥BE”,
那么原结论还成立吗?若成立,请证明;若不成立,请
说明理由.1、如图:已知AB∥DE,AC∥DF,BE=CF。求证:△ABC≌△DEF。考考你证明:∵ BE=CF(已知) ∴BC=EF(等式性质) ∠B=∠E 在△ABC和△DEF中BC=EF ∠C=∠F∴△ABC≌△DEF(ASA)∵ AB∥DE AC∥DF (已知) ∴ ∠B=∠DEF , ∠ACB=∠F2.(潼南·中考)如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连结AG,点E、F分别在AG上,连接BE、DF,∠1=∠2 , ∠3=∠4.
(1)证明:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长.【解析】 (1)∵四边形ABCD是正方形,∴AB=AD.
在△ABE和△DAF中,
∴△ABE≌△DAF(ASA).
(2)∵四边形ABCD是正方形,∴∠1+∠4=90°, ∵∠3=∠4,∴∠1+∠3=90°,∴∠AFD=90°,
在正方形ABCD中,AD∥BC,∴∠1=∠AGB=30°,
在Rt△ADF中,∠AFD=90°, AD=2,∴AF= ,DF =1,
由(1)得△ABE≌△DAF.∴AE=DF=1,∴EF=AF-AE= .1、边边边(SSS):三边对应相等
2、边角边(SAS):两边及夹角对应相等
3、角边角(ASA):ASA两角夹边对应相等
4、角角边(AAS):两角及一角的对边对应相等判定三角形全等的四种方法,它们分别是:
2.会用“ASA”和“AAS”判定方法证明两个三角形全等. 1.什么是全等三角形?2.我们已经学过了哪几种判定两个三角形全等的方法?能够完全重合的两个三角形叫做全等三角形.边边边(SSS)和边角边(SAS)结论:两角及夹边对应相等的两个三角形全等(ASA)A′EDCB′′先任意画一个△ABC.再画一个△A′B′C′.使A′B′=AB.∠A′= ∠A.
∠B′=∠B.(即两角和它们的夹边对应相等).把画好的△A′B′C′.剪下,放到△ABC上,它们全等吗?1、画A′B′=AB .
2、在A′B′同旁画∠DA′B′=∠A.∠EB′A′=∠B.
A′D.B′E交于点C′.探究如何用符号语言来表达呢?证明:在△ABC与△A B C 中∠A=∠A AB=A B∴△ABC≌△A’B’C’(ASA)ACB′′′′′′∠B=∠B′两角及夹边对应相等的两个三角形全等(ASA).证明:在△ABE 和△ACD 中,∴△ABE ≌△ACD(ASA).
∴AE =AD. 例1:如图,点D 在AB上,点E 在AC上,BA =AC,∠B =∠C.
求证:AD =AE. ACBEDF分析:能否转化为ASA?证明:∵ ∠A=∠D, ∠B=∠E(已知) ∴∠C=∠F(三角形内角和定理)∠B=∠E
BC=EF
∠C=∠F在△ABC和△DEF中∴△ABC≌△DEF(ASA)你能从上题中得到什么结论?两角及一角的对边对应相等的两个三角形全等(AAS)例2:在△ABC和△DEF中, ∠A=∠D, ∠B=∠E,BC=EF, △ABC和△DEF全等吗?为什么?如何用符号语言来表达呢?证明:在△ABC与△A B C 中∠A=∠A∴△ABC≌△A’B’C’(AAS)ACB′′′′∠B=∠B′问题3 如图,小明、小强一起踢球,不小心把一块三角形的装饰玻璃踢碎了,摔成了3 块,两人决定赔偿.你能告诉他们只带其中哪一块去玻璃店,就可以买到一块完全一样的玻璃吗?1、如图,要测量河两岸相对两点A,B两点的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得DE的长就是AB的长,为什么?12ABCD2、如图,AB⊥BC, AD⊥DC ,∠1= ∠2,
求证:AB=AD在△ABD和△ABC中
∠1=∠2 (已知)
∠C=∠D (已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)1.已知,如图,∠1=∠2,∠C=∠D,求证:AC=AD12【证明】证明:∵ ∠DAB =∠EAC,
∴ ∠DAC =∠EAB.
∵ AE⊥BE,AD⊥DC,
∴ ∠D =∠E =90°.
在△ADC 和△AEB 中, 例2 如图,AE⊥BE,AD⊥DC,CD =BE,∠DAB
=∠EAC.求证:AB =AC. ∴ △ADC ≌△AEB(AAS).
∴ AC =AB. 例2 如图,AE⊥BE,AD⊥DC,CD =BE,∠DAB
=∠EAC.求证:AB =AC. 证明:例1 、如图 ,AB=AC,∠B=∠C,那么△ABE和△ACD全等吗?为什么?证明: 在△ABE与△ACD中
∠B=∠C (已知)
AB=AC (已知)
∠A= ∠A (公共角)
∴ △ABE ≌△ACD (ASA) 1.如图,AD=AE,∠B=∠C,那么BE和CD相等么?为什么?变一变BE=CD你还能得出其他
什么结论?O 练习 如图,E,F 在线段AC上,AD∥CB,AE =
CF.若∠B =∠D,求证:DF =BE.证明:∵ AD∥CB ,
∴ ∠A =∠C.
∵ AE =CF ,
∴ AF =CE.
在△ADF 和△CBE 中, 练习 如图,E,F 在线段AC上,AD∥CB,AE =
CF.若∠B =∠D,求证:DF =BE.∴ △ADF ≌△CBE(AAS).
∴ DF =BE.证明: 变式 若将条件 “∠B =∠D”变为“DF∥BE”,
那么原结论还成立吗?若成立,请证明;若不成立,请
说明理由.1、如图:已知AB∥DE,AC∥DF,BE=CF。求证:△ABC≌△DEF。考考你证明:∵ BE=CF(已知) ∴BC=EF(等式性质) ∠B=∠E 在△ABC和△DEF中BC=EF ∠C=∠F∴△ABC≌△DEF(ASA)∵ AB∥DE AC∥DF (已知) ∴ ∠B=∠DEF , ∠ACB=∠F2.(潼南·中考)如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连结AG,点E、F分别在AG上,连接BE、DF,∠1=∠2 , ∠3=∠4.
(1)证明:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长.【解析】 (1)∵四边形ABCD是正方形,∴AB=AD.
在△ABE和△DAF中,
∴△ABE≌△DAF(ASA).
(2)∵四边形ABCD是正方形,∴∠1+∠4=90°, ∵∠3=∠4,∴∠1+∠3=90°,∴∠AFD=90°,
在正方形ABCD中,AD∥BC,∴∠1=∠AGB=30°,
在Rt△ADF中,∠AFD=90°, AD=2,∴AF= ,DF =1,
由(1)得△ABE≌△DAF.∴AE=DF=1,∴EF=AF-AE= .1、边边边(SSS):三边对应相等
2、边角边(SAS):两边及夹角对应相等
3、角边角(ASA):ASA两角夹边对应相等
4、角角边(AAS):两角及一角的对边对应相等判定三角形全等的四种方法,它们分别是:
