13.1.2线段垂直平分线性质 课件
文档属性
| 名称 | 13.1.2线段垂直平分线性质 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 486.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-12 21:08:24 | ||
图片预览





文档简介
课件34张PPT。§13.1.2 线段垂直平分线的性质1.了解轴对称及线段垂直平分线的性质和判定.
2.会应用线段垂直平分线的性质和判定解题.
3.依据轴对称的性质找出两个图形成轴对称及轴对称图形的对称轴.
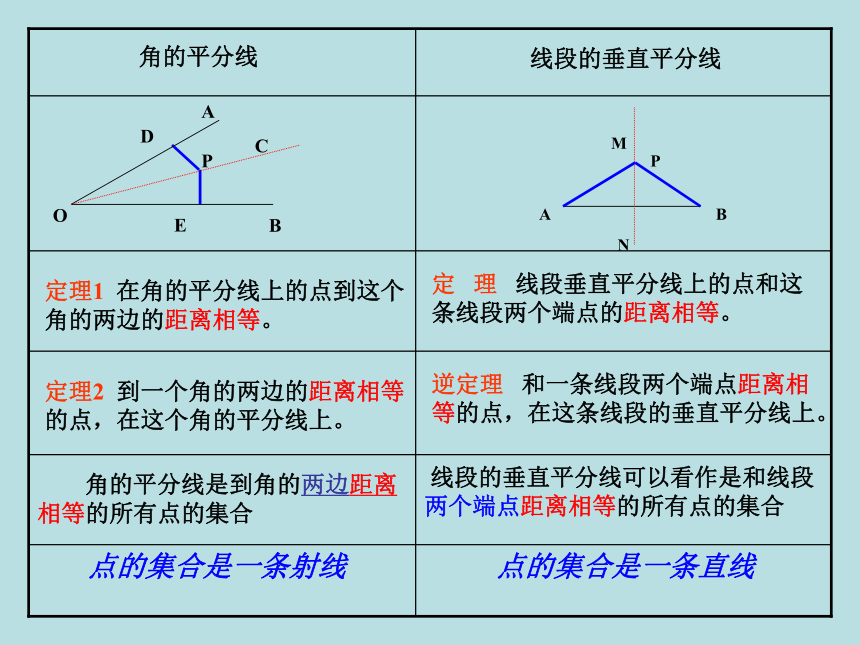
4.作出轴对称图形的对称轴,即线段垂直平分线的尺规作图.如果一个平面图形沿一条直线 .直线两旁的部分能够 ,这个图形就叫做轴对称图形.折痕所在的这条直线叫做_________. 对称轴折叠互相重合忆一忆把一个图形沿着某一条直线_______,如果它能够______________________,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做_________.折叠与另一个图形重合对称点画线段AB的垂直平分线l,在l上任意取点P,量一量点P到A与B的距离.你有什么发现?再取几个点试试.你能说明理由吗?PAB┓发现: P到A的距离与P到B的距离相等.C已知:如图.AC=BC. PC⊥AB,P是MN上任意一点.求证:PA=PB.∴△PCA≌△PCB(SAS)
∴PA=PB(全等三角形的对应边相等)证明:∵MN⊥AB,
∴ ∠PCA=∠PCB=90°在△APC与△BPC中:PC=PC(公共边)
∠PCA=∠PCB(已证)
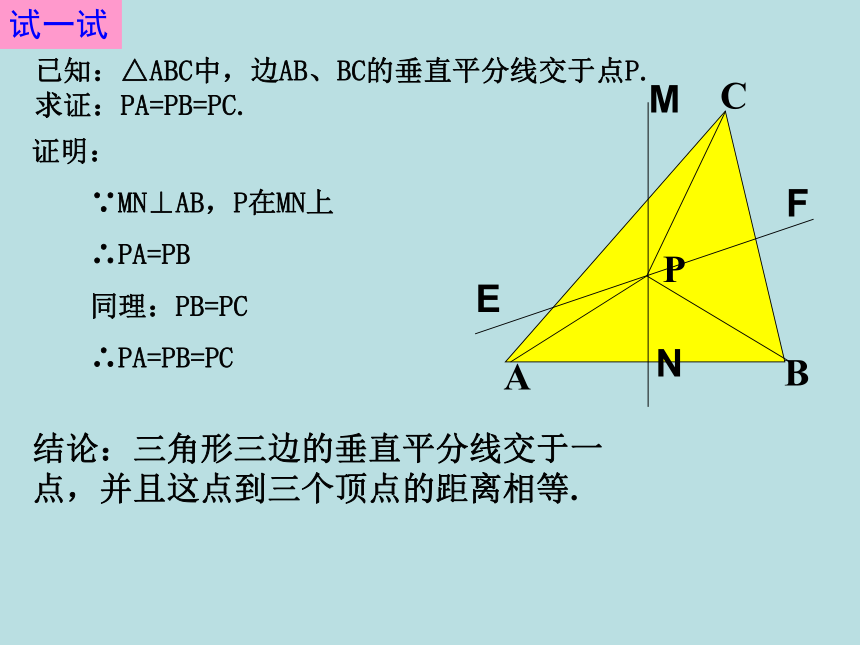
AC=BC(已知)反过来,若AP=BP,则P在线段AB的垂直平分线上.结论:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.AB已知: 两点A、B,和点A、B的距离相等的点应在什么位置?性质定理:在线段垂直平分线上的点到线段两个端点距离都相等.逆定理:与线段两个端点距离相等的点都在线段的垂直平分线上.线段垂直平分线可以看作是与线段两个端点距离相等的所有点的集合.常用于证明线段相等定理1 在角的平分线上的点到这个角的两边的距离相等。定理2 到一个角的两边的距离相等的点,在这个角的平分线上。 角的平分线是到角的两边距离相等的所有点的集合线段的垂直平分线定 理 线段垂直平分线上的点和这条线段两个端点的距离相等。逆定理 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。 线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合ABMNP点的集合是一条射线点的集合是一条直线结论:三角形三边的垂直平分线交于一 点,并且这点到三个顶点的距离相等.证明:
∵MN⊥AB,P在MN上
∴PA=PB
同理:PB=PC
∴PA=PB=PCMFEN已知:△ABC中,边AB、BC的垂直平分线交于点P.
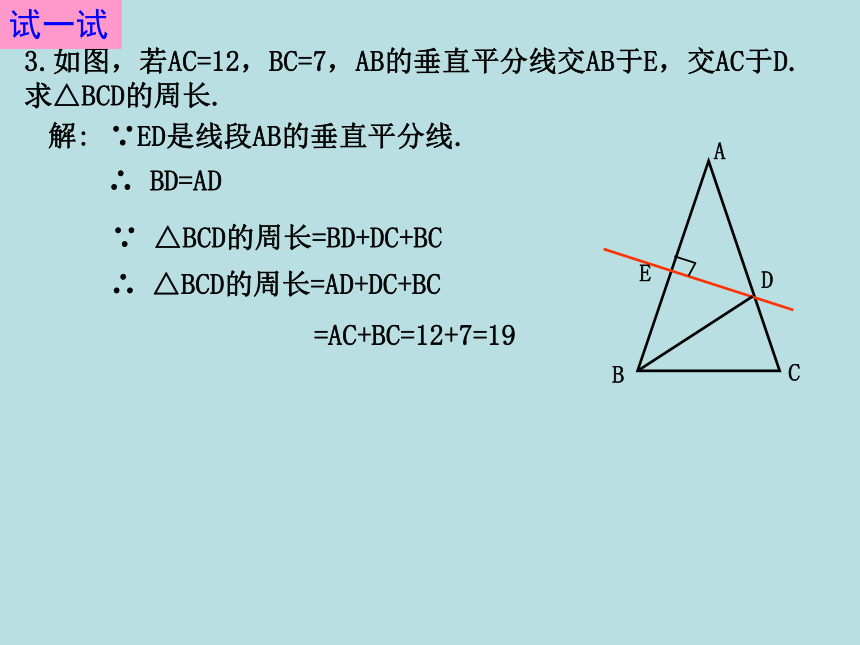
求证:PA=PB=PC.试一试DCBEA3.如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D.求△BCD的周长.∵ED是线段AB的垂直平分线.解:∴ BD=AD∵ △BCD的周长=BD+DC+BC∴ △BCD的周长=AD+DC+BC=AC+BC=12+7=19试一试1.在直线AB的另一侧任取一点K.
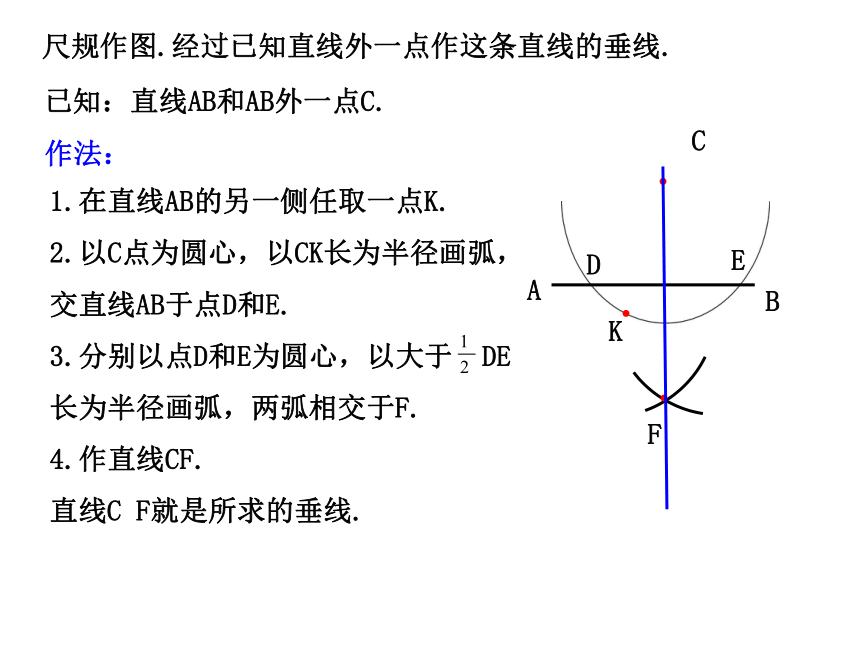
2.以C点为圆心,以CK长为半径画弧,交直线AB于点D和E.
3.分别以点D和E为圆心,以大于 DE长为半径画弧,两弧相交于F.
4.作直线CF.
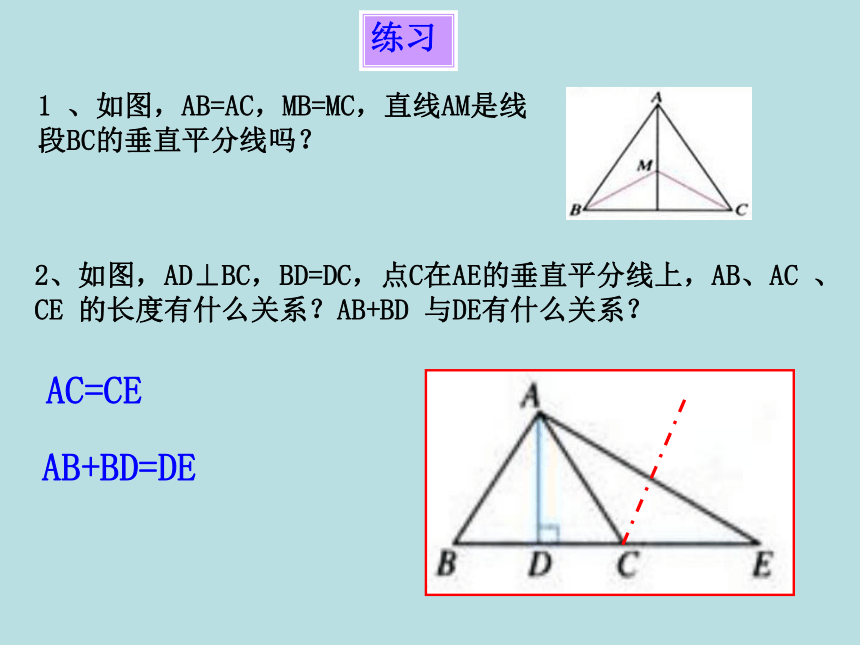
直线C F就是所求的垂线.尺规作图.经过已知直线外一点作这条直线的垂线.已知:直线AB和AB外一点C.作法:ABCKDEF2、如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC 、CE 的长度有什么关系?AB+BD 与DE有什么关系?AC=CEAB+BD=DE1 、如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?练习2.如图,NM是线段AB的垂直平分线,下列说
法正确的有: .
①AB⊥MN,②AD=DB, ③MN⊥AB,
④MD=DN,⑤AB是MN的垂直平分线.①②③1.下列说法:
①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB;
②若PA=PB,EA=EB,则直线PE垂直平分线段AB;
③若PA=PB,则点P必是线段AB的垂直平分线上的点;
④若EA=EB,则过点E的直线垂直平分线段AB.
其中正确的个数有 ( )
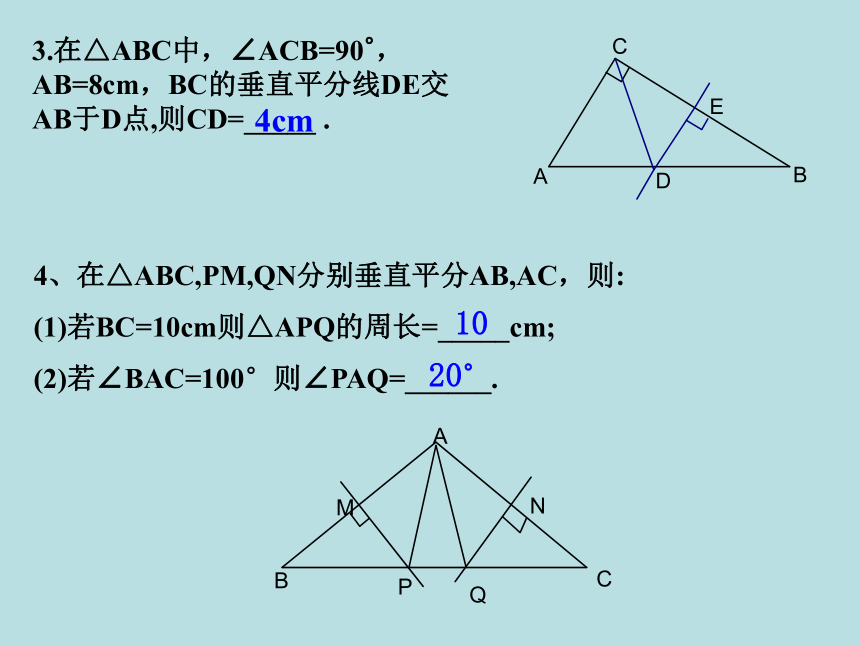
A.1个 B.2个 C.3个 D.4个C练一练3.在△ABC中,∠ACB=90°,AB=8cm,BC的垂直平分线DE交AB于D点,则CD=_____ .4cm4、在△ABC,PM,QN分别垂直平分AB,AC,则:
(1)若BC=10cm则△APQ的周长=_____cm;
(2)若∠BAC=100°则∠PAQ=______. 1020°6、如图,在△ABC中,ED垂直平分AB,
1) 若BD=10,则AD= .
2) 若∠A=50°,则∠ABD= .
3) 若AC=14,△BCD的周长为24,则BC= .
5、如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长.小结1、性质定理:线段垂直平分线上的点和这条线段两个端点
的距离相等.2、逆定理:和一条线段两个端点距离相等的点,在这条线
段的垂直平分线上.3、线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是和线段两个端点距离相等
的所有点的集合.好好学习天天向上第二课时§13.1.2 线段垂直平分线的性质1.能用尺规作线段的垂直平分线.
2.进一步了解作图的一般步骤和作图语言,了解作图的依据.
3.运用尺规作图的方法解决简单的作图问题.
学习重点:
作线段的垂直平分线. 轴对称的性质是什么? 如何判断一条直线是否是线段的垂直平分线? 说一说 线段垂直平分线的性质. 忆一忆(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作一个角的平分线;
(4)经过已知直线外一点作这条直线的垂线. 那么利用尺规还能解决什么作图问题呢? 我们已能用尺规完成:不折叠图形,你能准确地作出轴对称图形的对称轴吗? 有时我们感觉两个平面图形是轴对称的,如何验证呢?如果两个图形成轴对称,怎样作出图形的对称轴? 如果两个图形成轴对称,其对称轴是任何一对对应点所连线段的垂直平分线.因此.只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.作线段AB 的垂直平分线 例2 如图,点A 和点B 关于某条直线成轴对称,你能作出这条直线吗? 作法:连接A,B 1.分别以点A.B为圆心.以大于 AB的长为半径作弧,两弧相交于C,D 两点;2.作直线CD.
CD 就是所求作的直线. 这种作法的依据是什么?
这种作图方法还有哪些作用?
确定线段的中点. 如图中的五角星,请作出它的一条对称轴. 作轴对称图形的对称轴对于轴对称图形.只要找到任意一组对应点.作出对应点所连线段的垂直平分线.就得到此图形的对称轴.作法:
1.找出五角星的一对
对应点A和B,连接AB.
2.作出线段AB的垂直平分线n.
则n就是这个五角星的一条对称轴. AB五角星的对称轴有什么特点? 你能作出这个五角星的其他对称轴吗?它共有几条对称轴?相交于一点. 作轴对称图形的对称轴练习1.作出下列图形的一条对称轴.和同学比较一下.你们作出的对称轴一样吗?2.如图,角是轴对称图形吗?如果是,它的对称轴是什么?练习3.如图,与图形A 成轴对称的是哪个图形?画出它的对称轴.练习1.正方形ABCD边长为a,点E,F分别是对角线BD上的两点,过点E,F分别作AD,AB的平行线,如图所示,则图中阴影部分的面积之和等于 .做一做运用轴对称、转化的思想,阴影部分面积等于正方形面积的一半.2. 有A,B,C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置.ABC【提示】学校在连接任意两点的两条线段的垂直平分线的交点处.3.如图,如果△ACD的周长为18cm,△ABC的周长为28cm, DE是BC的垂直平分线,根据这些条件,你可以求出哪条线段的长? (1)△ACD的周长=AD +CD+AC=18cm.
(2)△ABC的周长=AB+AC+BC=28cm.(3)由DE是BC的垂直平分线得:BD=CD;
所以AD+CD=AD+BD=AB.(4)由(2)中式子-(1)中式子得BC=10cm.【解析】【提示】连接AB,作AB的垂直平分线,则与公路的交点就是要建的公共汽车站.4.如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?5.求作一点P,使它和已△ABC的三个顶点距离相等.·P解:试一试1.了解轴对称及线段的垂直平分线的有关性质.
2.会灵活运用这些性质来解决问题.
3.用尺规作出线段的垂直平分线.并据此得到作出一个
轴对称图形的一条对称轴的方法.
4.找出轴对称图形的任意一对对应点,连接这对对应点,
作出连线的垂直平分线,该垂直平分线就是这个轴对称图形
的一条对称轴.小结通过本课时的学习,需要我们:好好学习天天向上
2.会应用线段垂直平分线的性质和判定解题.
3.依据轴对称的性质找出两个图形成轴对称及轴对称图形的对称轴.
4.作出轴对称图形的对称轴,即线段垂直平分线的尺规作图.如果一个平面图形沿一条直线 .直线两旁的部分能够 ,这个图形就叫做轴对称图形.折痕所在的这条直线叫做_________. 对称轴折叠互相重合忆一忆把一个图形沿着某一条直线_______,如果它能够______________________,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做_________.折叠与另一个图形重合对称点画线段AB的垂直平分线l,在l上任意取点P,量一量点P到A与B的距离.你有什么发现?再取几个点试试.你能说明理由吗?PAB┓发现: P到A的距离与P到B的距离相等.C已知:如图.AC=BC. PC⊥AB,P是MN上任意一点.求证:PA=PB.∴△PCA≌△PCB(SAS)
∴PA=PB(全等三角形的对应边相等)证明:∵MN⊥AB,
∴ ∠PCA=∠PCB=90°在△APC与△BPC中:PC=PC(公共边)
∠PCA=∠PCB(已证)
AC=BC(已知)反过来,若AP=BP,则P在线段AB的垂直平分线上.结论:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.AB已知: 两点A、B,和点A、B的距离相等的点应在什么位置?性质定理:在线段垂直平分线上的点到线段两个端点距离都相等.逆定理:与线段两个端点距离相等的点都在线段的垂直平分线上.线段垂直平分线可以看作是与线段两个端点距离相等的所有点的集合.常用于证明线段相等定理1 在角的平分线上的点到这个角的两边的距离相等。定理2 到一个角的两边的距离相等的点,在这个角的平分线上。 角的平分线是到角的两边距离相等的所有点的集合线段的垂直平分线定 理 线段垂直平分线上的点和这条线段两个端点的距离相等。逆定理 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。 线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合ABMNP点的集合是一条射线点的集合是一条直线结论:三角形三边的垂直平分线交于一 点,并且这点到三个顶点的距离相等.证明:
∵MN⊥AB,P在MN上
∴PA=PB
同理:PB=PC
∴PA=PB=PCMFEN已知:△ABC中,边AB、BC的垂直平分线交于点P.
求证:PA=PB=PC.试一试DCBEA3.如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D.求△BCD的周长.∵ED是线段AB的垂直平分线.解:∴ BD=AD∵ △BCD的周长=BD+DC+BC∴ △BCD的周长=AD+DC+BC=AC+BC=12+7=19试一试1.在直线AB的另一侧任取一点K.
2.以C点为圆心,以CK长为半径画弧,交直线AB于点D和E.
3.分别以点D和E为圆心,以大于 DE长为半径画弧,两弧相交于F.
4.作直线CF.
直线C F就是所求的垂线.尺规作图.经过已知直线外一点作这条直线的垂线.已知:直线AB和AB外一点C.作法:ABCKDEF2、如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC 、CE 的长度有什么关系?AB+BD 与DE有什么关系?AC=CEAB+BD=DE1 、如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?练习2.如图,NM是线段AB的垂直平分线,下列说
法正确的有: .
①AB⊥MN,②AD=DB, ③MN⊥AB,
④MD=DN,⑤AB是MN的垂直平分线.①②③1.下列说法:
①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB;
②若PA=PB,EA=EB,则直线PE垂直平分线段AB;
③若PA=PB,则点P必是线段AB的垂直平分线上的点;
④若EA=EB,则过点E的直线垂直平分线段AB.
其中正确的个数有 ( )
A.1个 B.2个 C.3个 D.4个C练一练3.在△ABC中,∠ACB=90°,AB=8cm,BC的垂直平分线DE交AB于D点,则CD=_____ .4cm4、在△ABC,PM,QN分别垂直平分AB,AC,则:
(1)若BC=10cm则△APQ的周长=_____cm;
(2)若∠BAC=100°则∠PAQ=______. 1020°6、如图,在△ABC中,ED垂直平分AB,
1) 若BD=10,则AD= .
2) 若∠A=50°,则∠ABD= .
3) 若AC=14,△BCD的周长为24,则BC= .
5、如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长.小结1、性质定理:线段垂直平分线上的点和这条线段两个端点
的距离相等.2、逆定理:和一条线段两个端点距离相等的点,在这条线
段的垂直平分线上.3、线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是和线段两个端点距离相等
的所有点的集合.好好学习天天向上第二课时§13.1.2 线段垂直平分线的性质1.能用尺规作线段的垂直平分线.
2.进一步了解作图的一般步骤和作图语言,了解作图的依据.
3.运用尺规作图的方法解决简单的作图问题.
学习重点:
作线段的垂直平分线. 轴对称的性质是什么? 如何判断一条直线是否是线段的垂直平分线? 说一说 线段垂直平分线的性质. 忆一忆(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作一个角的平分线;
(4)经过已知直线外一点作这条直线的垂线. 那么利用尺规还能解决什么作图问题呢? 我们已能用尺规完成:不折叠图形,你能准确地作出轴对称图形的对称轴吗? 有时我们感觉两个平面图形是轴对称的,如何验证呢?如果两个图形成轴对称,怎样作出图形的对称轴? 如果两个图形成轴对称,其对称轴是任何一对对应点所连线段的垂直平分线.因此.只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.作线段AB 的垂直平分线 例2 如图,点A 和点B 关于某条直线成轴对称,你能作出这条直线吗? 作法:连接A,B 1.分别以点A.B为圆心.以大于 AB的长为半径作弧,两弧相交于C,D 两点;2.作直线CD.
CD 就是所求作的直线. 这种作法的依据是什么?
这种作图方法还有哪些作用?
确定线段的中点. 如图中的五角星,请作出它的一条对称轴. 作轴对称图形的对称轴对于轴对称图形.只要找到任意一组对应点.作出对应点所连线段的垂直平分线.就得到此图形的对称轴.作法:
1.找出五角星的一对
对应点A和B,连接AB.
2.作出线段AB的垂直平分线n.
则n就是这个五角星的一条对称轴. AB五角星的对称轴有什么特点? 你能作出这个五角星的其他对称轴吗?它共有几条对称轴?相交于一点. 作轴对称图形的对称轴练习1.作出下列图形的一条对称轴.和同学比较一下.你们作出的对称轴一样吗?2.如图,角是轴对称图形吗?如果是,它的对称轴是什么?练习3.如图,与图形A 成轴对称的是哪个图形?画出它的对称轴.练习1.正方形ABCD边长为a,点E,F分别是对角线BD上的两点,过点E,F分别作AD,AB的平行线,如图所示,则图中阴影部分的面积之和等于 .做一做运用轴对称、转化的思想,阴影部分面积等于正方形面积的一半.2. 有A,B,C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置.ABC【提示】学校在连接任意两点的两条线段的垂直平分线的交点处.3.如图,如果△ACD的周长为18cm,△ABC的周长为28cm, DE是BC的垂直平分线,根据这些条件,你可以求出哪条线段的长? (1)△ACD的周长=AD +CD+AC=18cm.
(2)△ABC的周长=AB+AC+BC=28cm.(3)由DE是BC的垂直平分线得:BD=CD;
所以AD+CD=AD+BD=AB.(4)由(2)中式子-(1)中式子得BC=10cm.【解析】【提示】连接AB,作AB的垂直平分线,则与公路的交点就是要建的公共汽车站.4.如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?5.求作一点P,使它和已△ABC的三个顶点距离相等.·P解:试一试1.了解轴对称及线段的垂直平分线的有关性质.
2.会灵活运用这些性质来解决问题.
3.用尺规作出线段的垂直平分线.并据此得到作出一个
轴对称图形的一条对称轴的方法.
4.找出轴对称图形的任意一对对应点,连接这对对应点,
作出连线的垂直平分线,该垂直平分线就是这个轴对称图形
的一条对称轴.小结通过本课时的学习,需要我们:好好学习天天向上
