10.1.2相交平面课件-2022-2023学年高二下学期数学沪教版(2020)必修第三册(共11张PPT)
文档属性
| 名称 | 10.1.2相交平面课件-2022-2023学年高二下学期数学沪教版(2020)必修第三册(共11张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 271.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 14:41:34 | ||
图片预览

文档简介
(共11张PPT)
10.1.2 相交平面
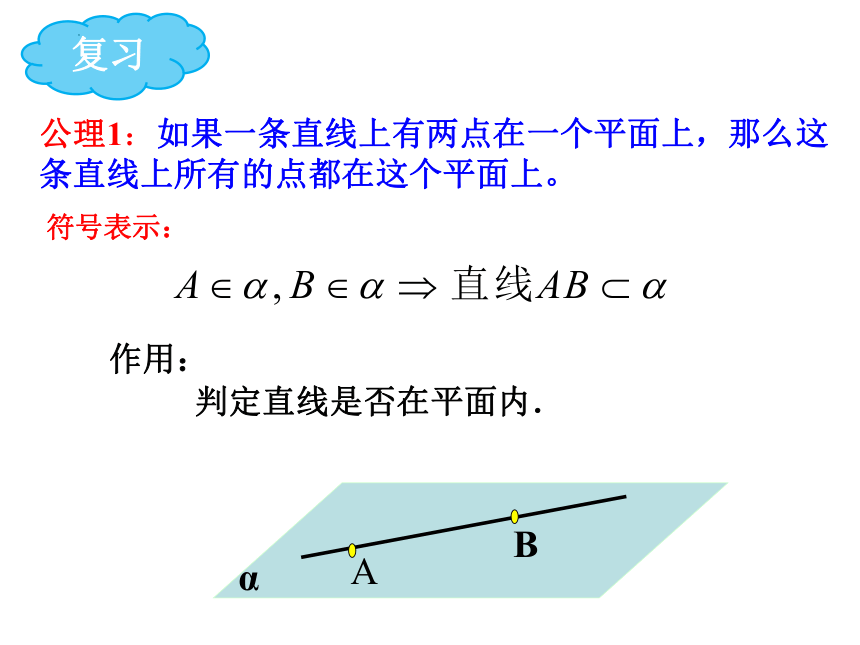
公理1:如果一条直线上有两点在一个平面上,那么这条直线上所有的点都在这个平面上。
α
A
B
符号表示:
作用:
判定直线是否在平面内.
复习
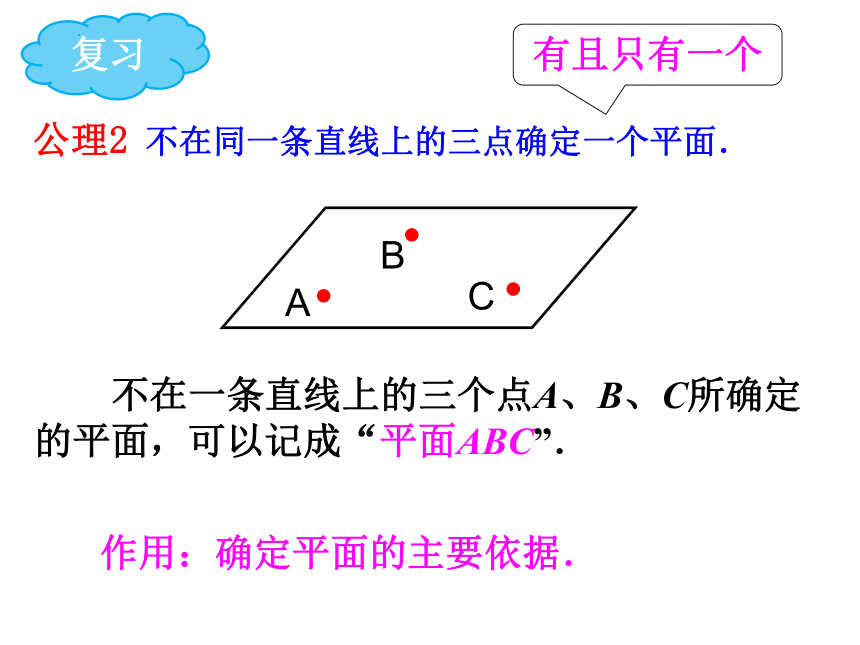
作用:确定平面的主要依据.
不在一条直线上的三个点A、B、C所确定的平面,可以记成“平面ABC”.
公理2 不在同一条直线上的三点确定一个平面.
有且只有一个
A
B
C
复习
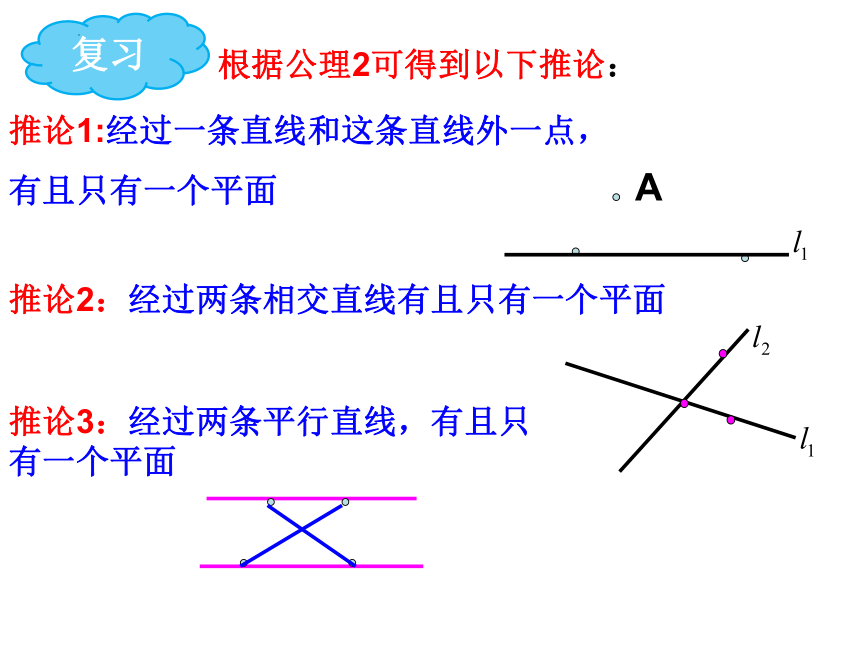
根据公理2可得到以下推论:
推论1:经过一条直线和这条直线外一点,
有且只有一个平面
A
推论2:经过两条相交直线有且只有一个平面
推论3:经过两条平行直线,有且只 有一个平面
复习
A
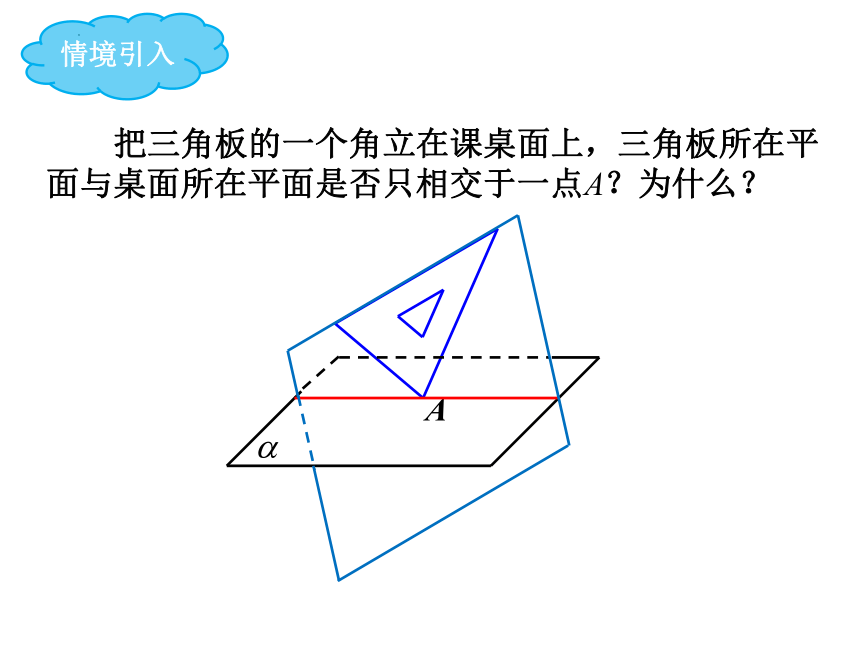
把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点A?为什么?
情境引入
公理3 如果两个平面有一个公共点,那么它们有且只有一条过该点的公共直线.
作用:
①判断两个平面相交的依据.
②判断点在直线上.
l
P
新课讲授
例3:如图,在长方体ABCD-A1B1C1D1中,找出下列各对平面的交线:
(1)平面ABCD与平面AA1B1B;
(2)平面A1BD与平面C1BD;
(3)平面ACC1A1与平面BDD1B1;
(4)平面ABCD与平面BB1D1.
例题讲解
练习1:画三个平面,使其中的两个平面互相平行,而第三个平面与这两个平面都相交.
巩固练习
练习2:用硬纸板作为平面的模型,摆出三个平面两两相交各种不同的情况.
巩固练习
练习3:如图,在长方体ABCD-A1B1C1D1中,
(1)设AC与BD的交点为O,O必为平面 与
平面 的公共点;
(2)画出平面A1BCD1与平面B1BDD1的交线.
巩固练习
课堂小结
公理3 如果两个平面有一个公共点,那么它们有且只有一条过该点的公共直线.
作用:
①判断两个平面相交的依据.
②判断点在直线上.
10.1.2 相交平面
公理1:如果一条直线上有两点在一个平面上,那么这条直线上所有的点都在这个平面上。
α
A
B
符号表示:
作用:
判定直线是否在平面内.
复习
作用:确定平面的主要依据.
不在一条直线上的三个点A、B、C所确定的平面,可以记成“平面ABC”.
公理2 不在同一条直线上的三点确定一个平面.
有且只有一个
A
B
C
复习
根据公理2可得到以下推论:
推论1:经过一条直线和这条直线外一点,
有且只有一个平面
A
推论2:经过两条相交直线有且只有一个平面
推论3:经过两条平行直线,有且只 有一个平面
复习
A
把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点A?为什么?
情境引入
公理3 如果两个平面有一个公共点,那么它们有且只有一条过该点的公共直线.
作用:
①判断两个平面相交的依据.
②判断点在直线上.
l
P
新课讲授
例3:如图,在长方体ABCD-A1B1C1D1中,找出下列各对平面的交线:
(1)平面ABCD与平面AA1B1B;
(2)平面A1BD与平面C1BD;
(3)平面ACC1A1与平面BDD1B1;
(4)平面ABCD与平面BB1D1.
例题讲解
练习1:画三个平面,使其中的两个平面互相平行,而第三个平面与这两个平面都相交.
巩固练习
练习2:用硬纸板作为平面的模型,摆出三个平面两两相交各种不同的情况.
巩固练习
练习3:如图,在长方体ABCD-A1B1C1D1中,
(1)设AC与BD的交点为O,O必为平面 与
平面 的公共点;
(2)画出平面A1BCD1与平面B1BDD1的交线.
巩固练习
课堂小结
公理3 如果两个平面有一个公共点,那么它们有且只有一条过该点的公共直线.
作用:
①判断两个平面相交的依据.
②判断点在直线上.
同课章节目录
