人教版(2019)选择性必修第一册 1.5 弹性碰撞和非弹性碰撞课件(共16张PPT)
文档属性
| 名称 | 人教版(2019)选择性必修第一册 1.5 弹性碰撞和非弹性碰撞课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-05-23 15:29:41 | ||
图片预览




文档简介
(共16张PPT)
5
弹性碰撞和非弹性碰撞
陨石撞地球
球拍打网球
碰撞是自然界常见的现象。陨石撞击地球而对地表产生破坏,网球受球拍撞击而改变运动状态……
物体碰撞中动量的变化情况,前面已进行了研究。那么,在各种碰撞中能量又是如何变化的?
问题
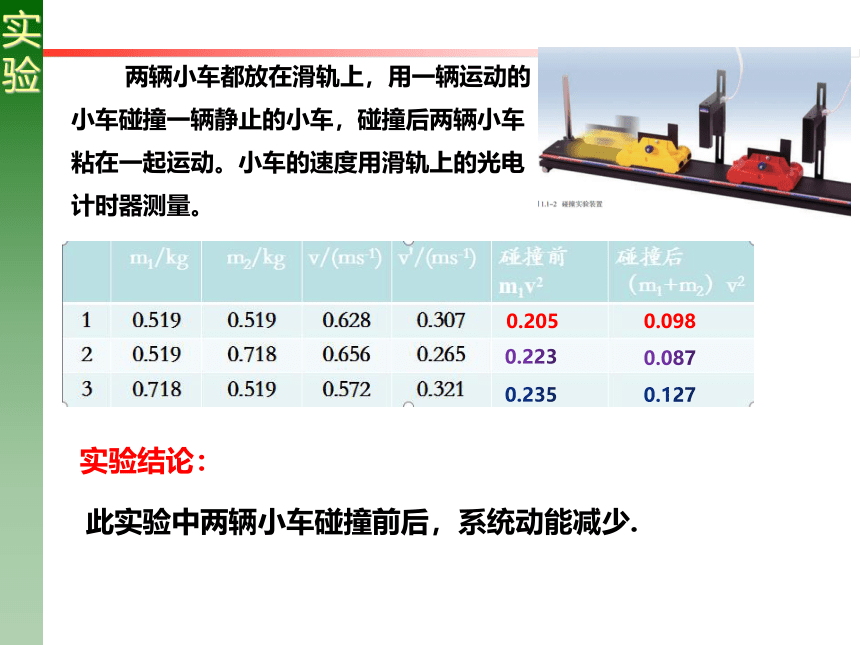
两辆小车都放在滑轨上,用一辆运动的小车碰撞一辆静止的小车,碰撞后两辆小车粘在一起运动。小车的速度用滑轨上的光电计时器测量。
实验
实验结论:
此实验中两辆小车碰撞前后,系统动能减少.
0.205
0.098
0.223
0.087
0.235
0.127
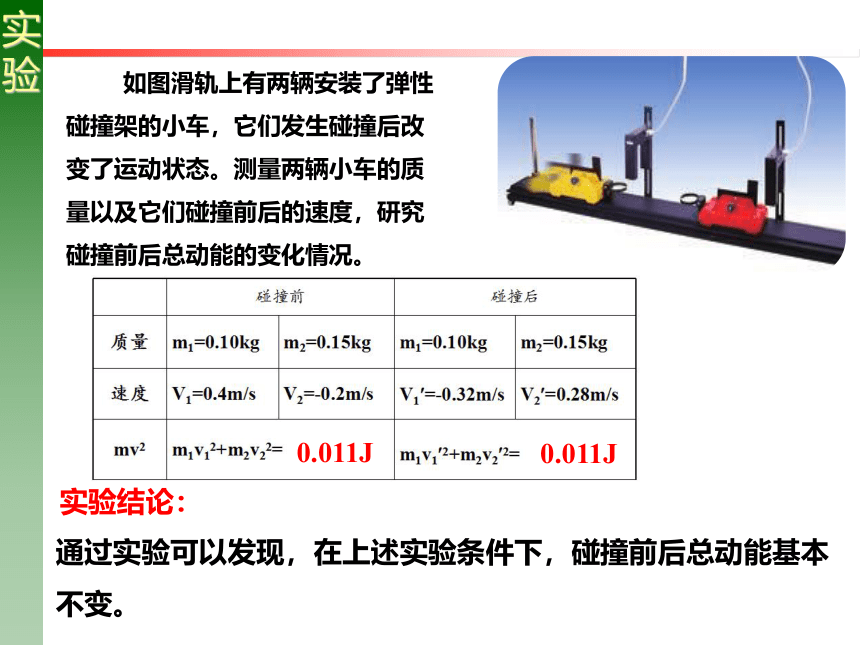
如图滑轨上有两辆安装了弹性碰撞架的小车,它们发生碰撞后改变了运动状态。测量两辆小车的质量以及它们碰撞前后的速度,研究碰撞前后总动能的变化情况。
实验
通过实验可以发现,在上述实验条件下,碰撞前后总动能基本不变。
实验结论:
0.011J
0.011J
如果系统在碰撞前后动能不变,这类碰撞叫作弹性碰撞。
弹性碰撞和非弹性碰撞
滑块碰撞后分开
弹性碰撞
授课
钢球、玻璃球碰撞时,动能损失很小,它们的碰撞可以看作弹性碰撞。
2.非弹性碰撞:
如果系统在碰撞后动能减少,这类碰撞叫作非弹性碰撞。
1.弹性碰撞:
特点:碰撞时物体的形变是弹性形变
特点:碰撞时物体的形变是非弹性形变
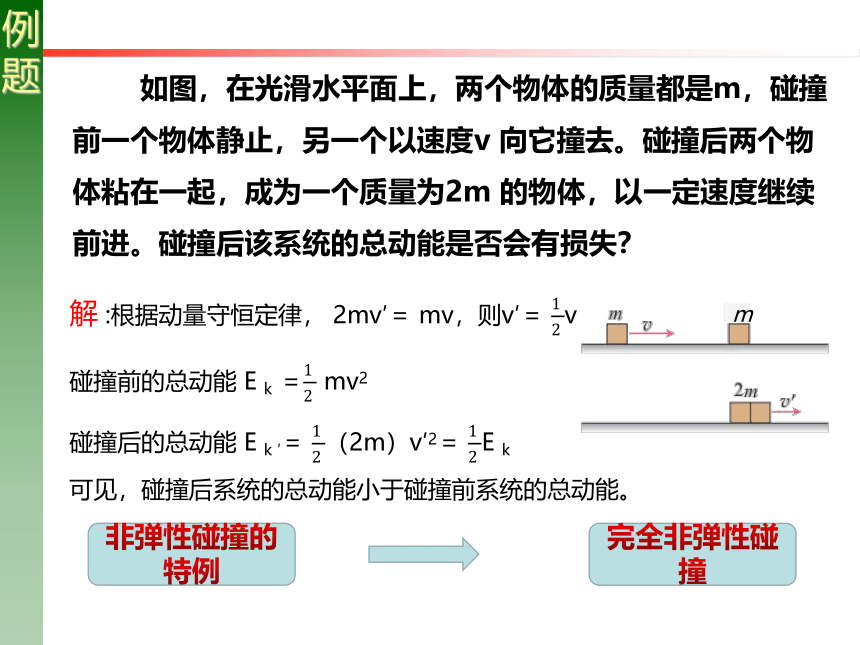
如图,在光滑水平面上,两个物体的质量都是m,碰撞前一个物体静止,另一个以速度v 向它撞去。碰撞后两个物体粘在一起,成为一个质量为2m 的物体,以一定速度继续前进。碰撞后该系统的总动能是否会有损失?
m
例题
如图,在光滑水平面上,两个物体的质量都是m,碰撞前一个物体静止,另一个以速度v 向它撞去。碰撞后两个物体粘在一起,成为一个质量为2m 的物体,以一定速度继续前进。碰撞后该系统的总动能是否会有损失?
m
解 :根据动量守恒定律, 2mv′= mv,则v′= v
碰撞前的总动能 E k = mv2
碰撞后的总动能 E k ′= (2m)v′2= E k
可见,碰撞后系统的总动能小于碰撞前系统的总动能。
非弹性碰撞的特例
完全非弹性碰撞
例题
碰撞后两物体合为一体或者具有共同速度,这种碰撞动能损失最大,称为完全非弹性碰撞。
特点:碰撞时物体的形变是非弹性形变,系统动量守恒,动能损失最大。
授课
3.完全非弹性碰撞:
对心碰撞:碰撞前后速度都沿同一条直线,即正碰
非对心碰撞:碰撞前后速度不沿同一条直线
v'1
m1
m2
v'2
v1
m1
m2
v1
m1
m2
v'1
m1
m2
v'2
碰撞的种类(从碰撞前后轨迹分类)
教授
弹性碰撞的实例分析:一动碰一静
碰前:m1速度v1,m2静止
碰后:m1速度v1′,m2速度v2 ′
动量守恒:
动能守恒:
m1
m2
m1
m2
v1
v1'
v2'
解得:
探究
1.若m1=m2时
2.若m1>>m2时
3.若m1<弹性碰撞的实例分析:一动碰一静
牛顿摆
保龄球击打球瓶
乒乓球撞篮球
讨论
1.系统动量守恒原则:碰撞前后系统的总动量守恒.
2.动能不增加原则:碰撞后系统的总动能小于或等于碰撞前系统的总动能,即系统的总动能不增加.
3.物理情景可行性原则:
①若碰前两物体同向运动,则应有v后>v前,碰后原来在前的物体速度一定增大,若碰后两物体同向运动,则应有v前′≥v后′。(否则碰撞没有结束,还要发生碰撞)
②碰前两物体相向运动,碰后两物体的运动方向不可能都不改变。
v1
m1
m2
v1′
m1
m2
v2′
碰撞三原则
规律
速度为 10 m/s 的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的 4 倍,碰撞是弹性的,求碰撞后两球的速度。
课后习题
速度为 10 m/s 的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的 4 倍,碰撞是弹性的,求碰撞后两球的速度。
答:以塑料球初速度的方向为正,设碰撞后塑料球和钢球的速度分别为 v′1 、 v′2,质量分别为 m1、m2,两球发生弹性碰撞,动量守恒,且机械能守恒,因此有:v′1= ,v′2= ,因为钢球的质量是塑料球的四倍,则有 4m1=m2 ,代入数据解得: v′1=- v1=-6m/s , v′2= v1=4 m/s 。
课后习题
在气垫导轨上,一个质量为 400 g 的滑块以 15 m/s 的速度与另一个质量为 200 g、速度为 10 m/s 并沿相反方向运动的滑块迎面相撞,碰撞后两个滑块粘在一起。
(1)求碰撞后滑块速度的大小和方向;
(2)这次碰撞,两滑块共损失了多少机械能?
课后习题
在气垫导轨上,一个质量为 400 g 的滑块以 15 m/s 的速度与另一个质量为 200 g、速度为 10 m/s 并沿相反方向运动的滑块迎面相撞,碰撞后两个滑块粘在一起。
(1)求碰撞后滑块速度的大小和方向;
(2)这次碰撞,两滑块共损失了多少机械能?
课后习题
答:(1)两滑块组成的系统动量守恒,以 0.4 kg的滑块运动的方向为正方向。由动量守恒定律可得:m1v1-m2v2=(m1+m2)v′,代入数据解得 v′= cm/s=6.7 cm/s
(2)ΔE= m1v12+ m2v22-(m1+m2)v′2,
代入数据解得: ΔE=4.2×10-3J
5
弹性碰撞和非弹性碰撞
陨石撞地球
球拍打网球
碰撞是自然界常见的现象。陨石撞击地球而对地表产生破坏,网球受球拍撞击而改变运动状态……
物体碰撞中动量的变化情况,前面已进行了研究。那么,在各种碰撞中能量又是如何变化的?
问题
两辆小车都放在滑轨上,用一辆运动的小车碰撞一辆静止的小车,碰撞后两辆小车粘在一起运动。小车的速度用滑轨上的光电计时器测量。
实验
实验结论:
此实验中两辆小车碰撞前后,系统动能减少.
0.205
0.098
0.223
0.087
0.235
0.127
如图滑轨上有两辆安装了弹性碰撞架的小车,它们发生碰撞后改变了运动状态。测量两辆小车的质量以及它们碰撞前后的速度,研究碰撞前后总动能的变化情况。
实验
通过实验可以发现,在上述实验条件下,碰撞前后总动能基本不变。
实验结论:
0.011J
0.011J
如果系统在碰撞前后动能不变,这类碰撞叫作弹性碰撞。
弹性碰撞和非弹性碰撞
滑块碰撞后分开
弹性碰撞
授课
钢球、玻璃球碰撞时,动能损失很小,它们的碰撞可以看作弹性碰撞。
2.非弹性碰撞:
如果系统在碰撞后动能减少,这类碰撞叫作非弹性碰撞。
1.弹性碰撞:
特点:碰撞时物体的形变是弹性形变
特点:碰撞时物体的形变是非弹性形变
如图,在光滑水平面上,两个物体的质量都是m,碰撞前一个物体静止,另一个以速度v 向它撞去。碰撞后两个物体粘在一起,成为一个质量为2m 的物体,以一定速度继续前进。碰撞后该系统的总动能是否会有损失?
m
例题
如图,在光滑水平面上,两个物体的质量都是m,碰撞前一个物体静止,另一个以速度v 向它撞去。碰撞后两个物体粘在一起,成为一个质量为2m 的物体,以一定速度继续前进。碰撞后该系统的总动能是否会有损失?
m
解 :根据动量守恒定律, 2mv′= mv,则v′= v
碰撞前的总动能 E k = mv2
碰撞后的总动能 E k ′= (2m)v′2= E k
可见,碰撞后系统的总动能小于碰撞前系统的总动能。
非弹性碰撞的特例
完全非弹性碰撞
例题
碰撞后两物体合为一体或者具有共同速度,这种碰撞动能损失最大,称为完全非弹性碰撞。
特点:碰撞时物体的形变是非弹性形变,系统动量守恒,动能损失最大。
授课
3.完全非弹性碰撞:
对心碰撞:碰撞前后速度都沿同一条直线,即正碰
非对心碰撞:碰撞前后速度不沿同一条直线
v'1
m1
m2
v'2
v1
m1
m2
v1
m1
m2
v'1
m1
m2
v'2
碰撞的种类(从碰撞前后轨迹分类)
教授
弹性碰撞的实例分析:一动碰一静
碰前:m1速度v1,m2静止
碰后:m1速度v1′,m2速度v2 ′
动量守恒:
动能守恒:
m1
m2
m1
m2
v1
v1'
v2'
解得:
探究
1.若m1=m2时
2.若m1>>m2时
3.若m1<
牛顿摆
保龄球击打球瓶
乒乓球撞篮球
讨论
1.系统动量守恒原则:碰撞前后系统的总动量守恒.
2.动能不增加原则:碰撞后系统的总动能小于或等于碰撞前系统的总动能,即系统的总动能不增加.
3.物理情景可行性原则:
①若碰前两物体同向运动,则应有v后>v前,碰后原来在前的物体速度一定增大,若碰后两物体同向运动,则应有v前′≥v后′。(否则碰撞没有结束,还要发生碰撞)
②碰前两物体相向运动,碰后两物体的运动方向不可能都不改变。
v1
m1
m2
v1′
m1
m2
v2′
碰撞三原则
规律
速度为 10 m/s 的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的 4 倍,碰撞是弹性的,求碰撞后两球的速度。
课后习题
速度为 10 m/s 的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的 4 倍,碰撞是弹性的,求碰撞后两球的速度。
答:以塑料球初速度的方向为正,设碰撞后塑料球和钢球的速度分别为 v′1 、 v′2,质量分别为 m1、m2,两球发生弹性碰撞,动量守恒,且机械能守恒,因此有:v′1= ,v′2= ,因为钢球的质量是塑料球的四倍,则有 4m1=m2 ,代入数据解得: v′1=- v1=-6m/s , v′2= v1=4 m/s 。
课后习题
在气垫导轨上,一个质量为 400 g 的滑块以 15 m/s 的速度与另一个质量为 200 g、速度为 10 m/s 并沿相反方向运动的滑块迎面相撞,碰撞后两个滑块粘在一起。
(1)求碰撞后滑块速度的大小和方向;
(2)这次碰撞,两滑块共损失了多少机械能?
课后习题
在气垫导轨上,一个质量为 400 g 的滑块以 15 m/s 的速度与另一个质量为 200 g、速度为 10 m/s 并沿相反方向运动的滑块迎面相撞,碰撞后两个滑块粘在一起。
(1)求碰撞后滑块速度的大小和方向;
(2)这次碰撞,两滑块共损失了多少机械能?
课后习题
答:(1)两滑块组成的系统动量守恒,以 0.4 kg的滑块运动的方向为正方向。由动量守恒定律可得:m1v1-m2v2=(m1+m2)v′,代入数据解得 v′= cm/s=6.7 cm/s
(2)ΔE= m1v12+ m2v22-(m1+m2)v′2,
代入数据解得: ΔE=4.2×10-3J
