人教版(2019)选择性必修第一册 1.5 碰撞 课件(共18张PPT)
文档属性
| 名称 | 人教版(2019)选择性必修第一册 1.5 碰撞 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-05-23 15:29:09 | ||
图片预览



文档简介
(共18张PPT)
碰撞
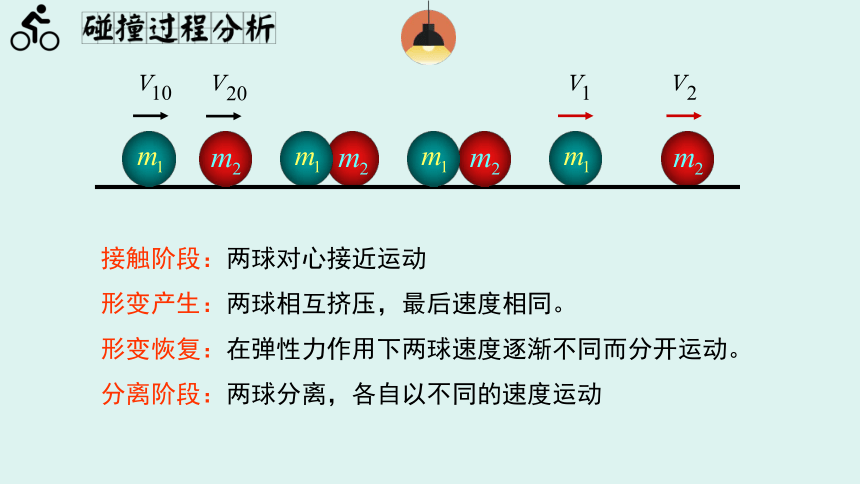
接触阶段:两球对心接近运动
形变产生:两球相互挤压,最后速度相同。
形变恢复:在弹性力作用下两球速度逐渐不同而分开运动。
分离阶段:两球分离,各自以不同的速度运动
一个钢球与另一个静止的钢球相碰,如果两个钢球的质量相等,第一个钢球停止运动,第二个钢球能摆到同样的高度,说明这个碰撞过程中没有能量损失,碰撞过程能量守恒。
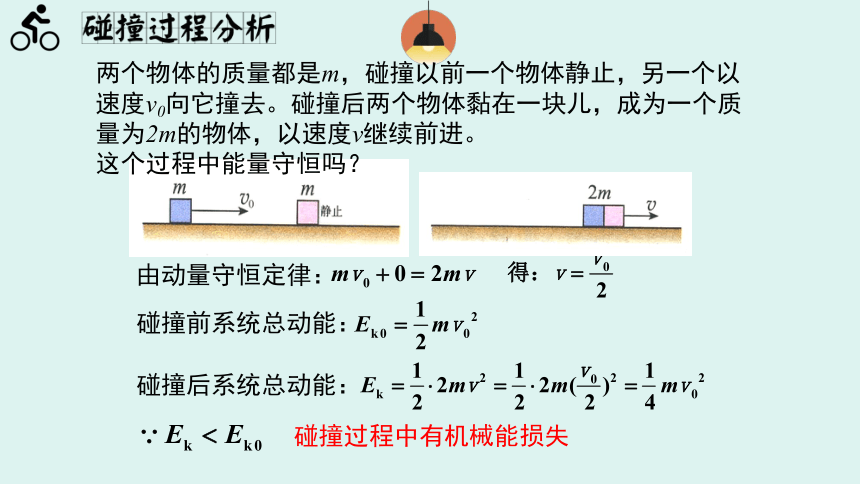
两个物体的质量都是m,碰撞以前一个物体静止,另一个以速度v0向它撞去。碰撞后两个物体黏在一块儿,成为一个质量为2m的物体,以速度v继续前进。
这个过程中能量守恒吗?
由动量守恒定律:
碰撞前系统总动能:
碰撞后系统总动能:
碰撞过程中有机械能损失
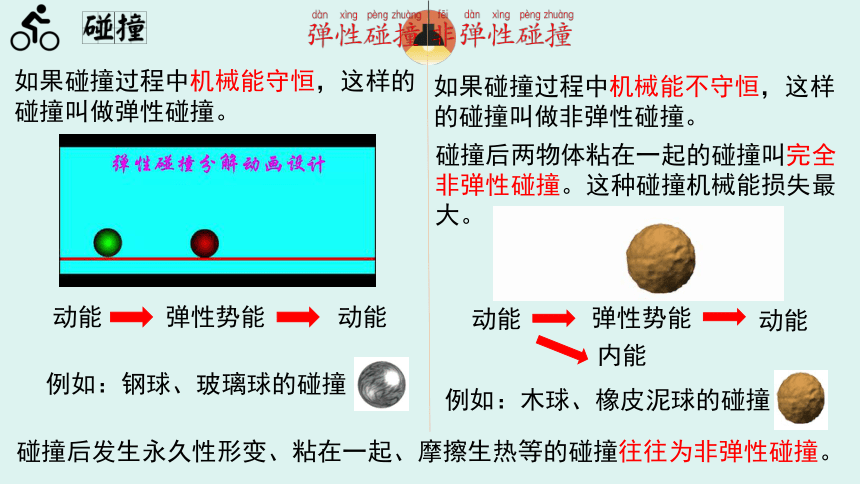
如果碰撞过程中机械能守恒,这样的碰撞叫做弹性碰撞。
如果碰撞过程中机械能不守恒,这样的碰撞叫做非弹性碰撞。
碰撞后两物体粘在一起的碰撞叫完全非弹性碰撞。这种碰撞机械能损失最大。
动能
动能
弹性势能
动能
动能
弹性势能
内能
例如:钢球、玻璃球的碰撞
例如:木球、橡皮泥球的碰撞
碰撞后发生永久性形变、粘在一起、摩擦生热等的碰撞往往为非弹性碰撞。
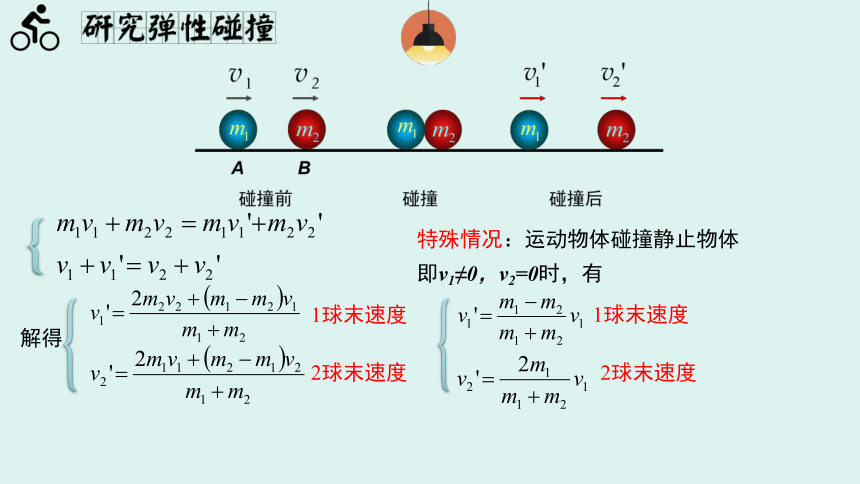
动量守恒
机械能守恒
整理得
解得
1球趋近2球的相对速度
2球远离1球的相对速度
等于
解得
1球末速度
2球末速度
特殊情况:运动物体碰撞静止物体
即v1≠0,v2=0时,有
1球末速度
2球末速度
碰后实现动量和动能的全部转移(即交换了速度)
碰后m1速度几乎没变,仍按原速度运动 ,质量小物体以m1的速度的两倍向前运动。
碰后m1被按原来速率弹回,m2几乎末动。
1.m1=m2
2.m1>>m2
3.m1<动量守恒
机械能有损失
或者
动量守恒
解得
机械能损失最大
1.系统动量守恒原则:碰撞前后系统的总动量守恒.
2.动能不增加原则:碰撞后系统的总动能小于或等于碰撞前系统的总动能,即系统的总动能不增加.
3.物理情景可行性原则:若碰后两物体同向运动,则碰撞后后面物体的速度一定小于或等于前面物体的速度(否则碰撞没有结束,还要发生碰撞).
1.对心碰撞
如图所示,一个运动的球与一个静止的球碰撞,碰撞之前球的运动速度与两球心在同一直线上,碰撞之后两球的速度仍会沿着这条直线。这种碰撞称为正碰,也叫对心碰撞。
2.非对心碰撞
一个运动的球与一个静止的球碰撞,碰撞之前球的运动速度与两球心的连线不在同一条直线上,碰撞之后两球的速度都会偏离原来两球心的连线。这种碰撞称为非对心碰撞,也叫斜碰。
与宏观物体碰撞不同的是,微观粒子相互接近时并不发生直接碰撞,因此微观粒子的碰撞又叫做散射。由于粒子与物质微粒发生对心碰撞的概率很小,所以多数粒子在碰撞后飞向四面八方。
金箔原子对粒子的散射
由于原子之间强大的相互作用,碰撞时原子相当于质量极大的物体,不会移动。
一弹丸在飞行到距离地面5 m高时仅有向右的水平速度v0=2 m/s,爆炸成为甲、乙两块水平飞出,甲、乙的质量比为3∶1.不计质量损失,取重力加速度g=10 m/s2.则下列图中两块弹片飞行的轨迹可能正确的是
√
在光滑水平面上,有A、B两个小球向右沿同一直线运动,取向右为正,两球的动量分别是pA=5kg·m/s,pB=7kg·m/s,如图所示.若能发生正碰,则碰后两球的动量增量△pA、△pB可能是 ( )
A.△pA=-3kg·m/s;△pB =3kg·m/s
B.△pA=3kg·m/s;△pB =3kg·m/s
C.△pA= -10kg·m/s;△pB =10kg·m/s D.△pA=3kg·m/s;△pB = -3kg·m/s
A
质量为m速度为v的A球,跟质量为3m的静止B球发生正碰,碰撞可能是弹性,也可能非弹性,碰后B球的速度可能是以下值吗?
(A)0.6v (B)0.4v (C)0.2v
解:B球速度的最小值发生在完全非弹性碰撞情形
由动量守恒:
B球速度的最大值发生在弹性碰撞时:
∵所以,只有0.4v是速度可能值
在光滑水平面上,一质量为m,速度大小为v的A球与质量为2m静止的B球碰撞后,A球的速度方向与碰撞前相反,则碰撞后B球的速度大小可能是
A.0.6v B.0.4v C.0.3v D.0.2v
√
A、B两球在水平方向上合外力为零,A球和B球碰撞的过程中动量守恒,设A、B两球碰撞后的速度分别为v1、v2,以v的方向为正方向,由动量守恒定律有:
mv=mv1+2mv2①,
假设碰后A球静止,即v1=0,可得v2=0.5v
由题意可知A被反弹,所以球B的速度有:v2>0.5v②
A、B两球碰撞过程能量可能有损失,由能量关系有:
碰撞
接触阶段:两球对心接近运动
形变产生:两球相互挤压,最后速度相同。
形变恢复:在弹性力作用下两球速度逐渐不同而分开运动。
分离阶段:两球分离,各自以不同的速度运动
一个钢球与另一个静止的钢球相碰,如果两个钢球的质量相等,第一个钢球停止运动,第二个钢球能摆到同样的高度,说明这个碰撞过程中没有能量损失,碰撞过程能量守恒。
两个物体的质量都是m,碰撞以前一个物体静止,另一个以速度v0向它撞去。碰撞后两个物体黏在一块儿,成为一个质量为2m的物体,以速度v继续前进。
这个过程中能量守恒吗?
由动量守恒定律:
碰撞前系统总动能:
碰撞后系统总动能:
碰撞过程中有机械能损失
如果碰撞过程中机械能守恒,这样的碰撞叫做弹性碰撞。
如果碰撞过程中机械能不守恒,这样的碰撞叫做非弹性碰撞。
碰撞后两物体粘在一起的碰撞叫完全非弹性碰撞。这种碰撞机械能损失最大。
动能
动能
弹性势能
动能
动能
弹性势能
内能
例如:钢球、玻璃球的碰撞
例如:木球、橡皮泥球的碰撞
碰撞后发生永久性形变、粘在一起、摩擦生热等的碰撞往往为非弹性碰撞。
动量守恒
机械能守恒
整理得
解得
1球趋近2球的相对速度
2球远离1球的相对速度
等于
解得
1球末速度
2球末速度
特殊情况:运动物体碰撞静止物体
即v1≠0,v2=0时,有
1球末速度
2球末速度
碰后实现动量和动能的全部转移(即交换了速度)
碰后m1速度几乎没变,仍按原速度运动 ,质量小物体以m1的速度的两倍向前运动。
碰后m1被按原来速率弹回,m2几乎末动。
1.m1=m2
2.m1>>m2
3.m1<
机械能有损失
或者
动量守恒
解得
机械能损失最大
1.系统动量守恒原则:碰撞前后系统的总动量守恒.
2.动能不增加原则:碰撞后系统的总动能小于或等于碰撞前系统的总动能,即系统的总动能不增加.
3.物理情景可行性原则:若碰后两物体同向运动,则碰撞后后面物体的速度一定小于或等于前面物体的速度(否则碰撞没有结束,还要发生碰撞).
1.对心碰撞
如图所示,一个运动的球与一个静止的球碰撞,碰撞之前球的运动速度与两球心在同一直线上,碰撞之后两球的速度仍会沿着这条直线。这种碰撞称为正碰,也叫对心碰撞。
2.非对心碰撞
一个运动的球与一个静止的球碰撞,碰撞之前球的运动速度与两球心的连线不在同一条直线上,碰撞之后两球的速度都会偏离原来两球心的连线。这种碰撞称为非对心碰撞,也叫斜碰。
与宏观物体碰撞不同的是,微观粒子相互接近时并不发生直接碰撞,因此微观粒子的碰撞又叫做散射。由于粒子与物质微粒发生对心碰撞的概率很小,所以多数粒子在碰撞后飞向四面八方。
金箔原子对粒子的散射
由于原子之间强大的相互作用,碰撞时原子相当于质量极大的物体,不会移动。
一弹丸在飞行到距离地面5 m高时仅有向右的水平速度v0=2 m/s,爆炸成为甲、乙两块水平飞出,甲、乙的质量比为3∶1.不计质量损失,取重力加速度g=10 m/s2.则下列图中两块弹片飞行的轨迹可能正确的是
√
在光滑水平面上,有A、B两个小球向右沿同一直线运动,取向右为正,两球的动量分别是pA=5kg·m/s,pB=7kg·m/s,如图所示.若能发生正碰,则碰后两球的动量增量△pA、△pB可能是 ( )
A.△pA=-3kg·m/s;△pB =3kg·m/s
B.△pA=3kg·m/s;△pB =3kg·m/s
C.△pA= -10kg·m/s;△pB =10kg·m/s D.△pA=3kg·m/s;△pB = -3kg·m/s
A
质量为m速度为v的A球,跟质量为3m的静止B球发生正碰,碰撞可能是弹性,也可能非弹性,碰后B球的速度可能是以下值吗?
(A)0.6v (B)0.4v (C)0.2v
解:B球速度的最小值发生在完全非弹性碰撞情形
由动量守恒:
B球速度的最大值发生在弹性碰撞时:
∵所以,只有0.4v是速度可能值
在光滑水平面上,一质量为m,速度大小为v的A球与质量为2m静止的B球碰撞后,A球的速度方向与碰撞前相反,则碰撞后B球的速度大小可能是
A.0.6v B.0.4v C.0.3v D.0.2v
√
A、B两球在水平方向上合外力为零,A球和B球碰撞的过程中动量守恒,设A、B两球碰撞后的速度分别为v1、v2,以v的方向为正方向,由动量守恒定律有:
mv=mv1+2mv2①,
假设碰后A球静止,即v1=0,可得v2=0.5v
由题意可知A被反弹,所以球B的速度有:v2>0.5v②
A、B两球碰撞过程能量可能有损失,由能量关系有:
