数学八年级上人教新课标(新版)11.3多边形及其内角和课件
文档属性
| 名称 | 数学八年级上人教新课标(新版)11.3多边形及其内角和课件 |  | |
| 格式 | zip | ||
| 文件大小 | 699.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-13 09:10:04 | ||
图片预览



文档简介
课件19张PPT。八年级 上册11.3 多边形及其内角和 (第1课时)课件说明本课是在学生已经学习了三角形的有关概念和性质
的基础上,利用学习三角形的经验方法进一步研究
多边形的有关概念和性质.学习目标:
1.了解多边形的有关概念,感悟类比方法的价值.
2.探索并证明多边形内角和公式,体会化归思想和
从具体到抽象的研究问题方法.
3.运用多边形内角和公式解决简单问题.
学习重点:
多边形内角和公式的探索与证明过程.
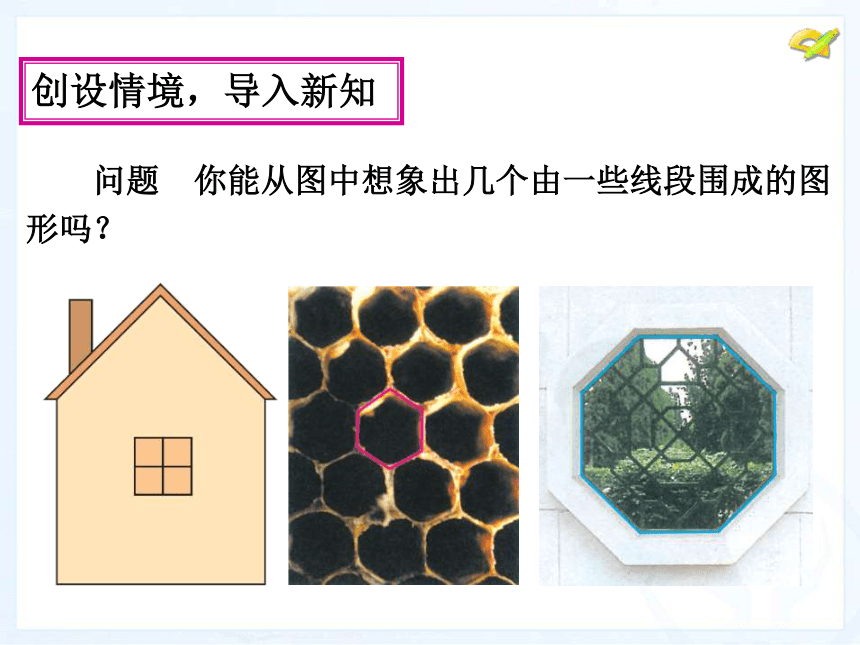
课件说明创设情境,导入新知 问题 你能从图中想象出几个由一些线段围成的图
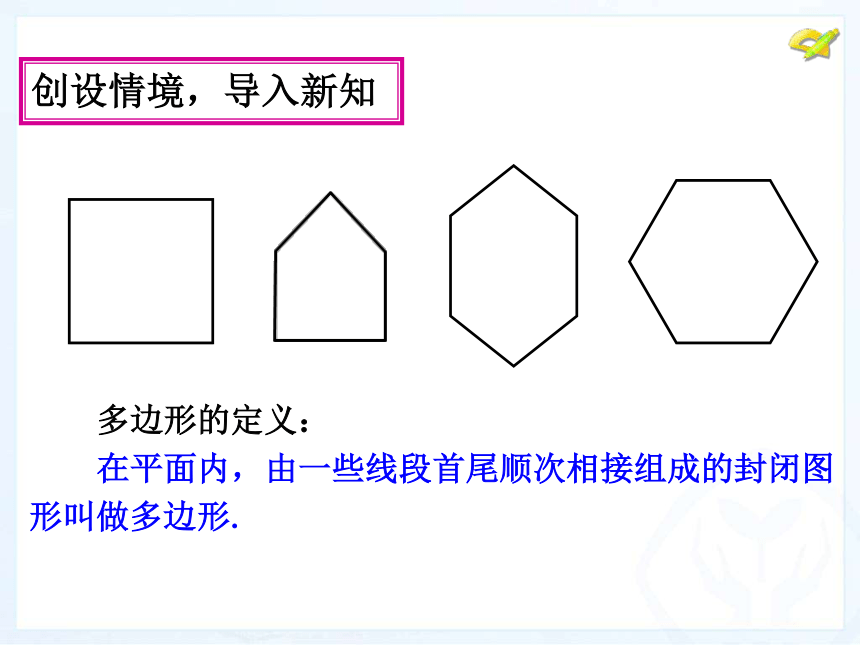
形吗?创设情境,导入新知 多边形的定义:
在平面内,由一些线段首尾顺次相接组成的封闭图
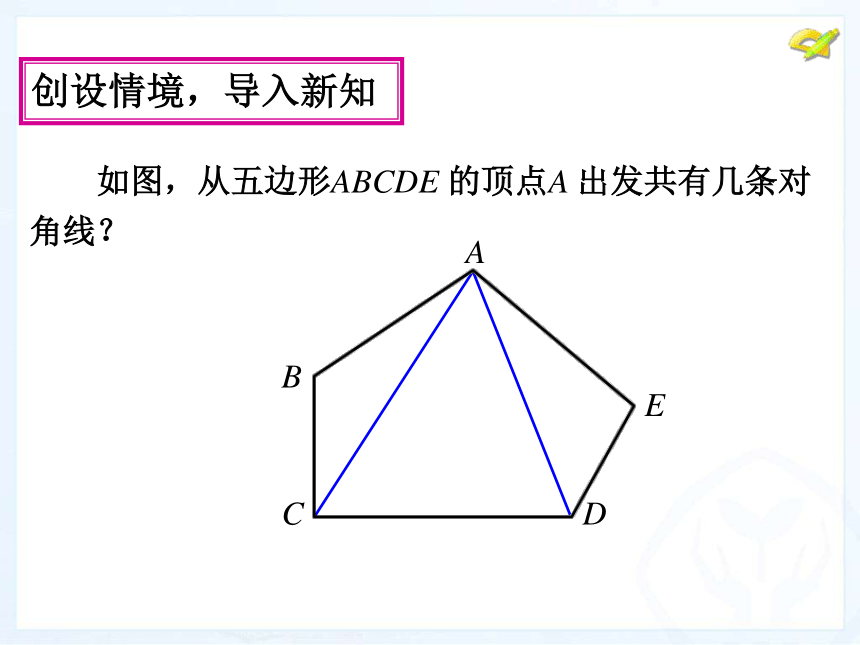
形叫做多边形.创设情境,导入新知 如图,从五边形ABCDE 的顶点A 出发共有几条对
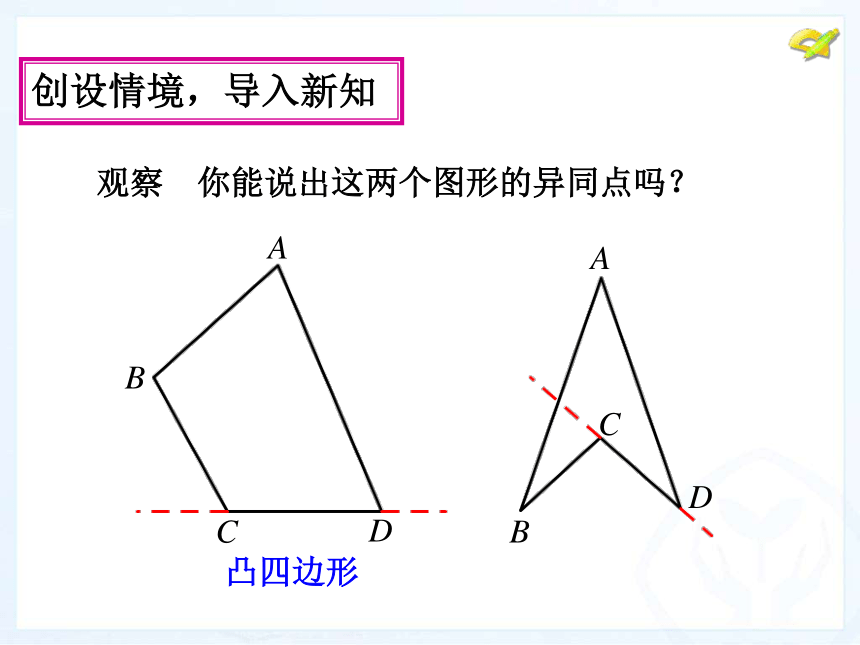
角线?凸四边形创设情境,导入新知 观察 你能说出这两个图形的异同点吗?创设情境,导入新知 想一想 正方形的边、角有什么特点?各个角都相等,各条边都相等的多边形叫做正多边形. 回忆 长方形、正方形的内角和等于______.360° 创设情境,导入新知 思考 任意一个四边形的内角和是否也等于360° 呢?动手操作,探究新知 探究 你能利用三角形内角和定理证明你的结论
吗?证明:连接AC,
∠BAD +∠B +∠BCD +∠D
=(∠BAC +∠BCA +∠B)
+ (∠DAC +∠DCA +∠D),
= 180° + 180° = 360° .动手操作,探究新知 探究 你能利用三角形内角和定理证明你的结论
吗? 从四边形的一个顶点出发,
可以作_____条对角线,它们将
四边形分为 个三角形,
四边形的内角和等于
180°×____= °.122360动手操作,探究新知 探究 类比前面的过程,你能探索五边形的内角和
吗?六边形呢? 如图,从五边形的一个顶点
出发,可以作 条对角线,它
们将五边形分为____个三角形,
五边形的内角和等于
180°× = °.233540动手操作,探究新知 如图,从六边形的一个顶点出发,可以作_____条
对角线,它们将六边形分为_____个三角形,六边形的
内角和等于180°×____=_______°.344720C 从n 边形的一个顶点出发,可以作(n -3)条对角
线,它们将n 边形分为(n -2)个三角形,这(n -2)
个三角形的内角和就是n 边形的内角和,所以,n 边形
的内角和等于(n -2)×180°.归纳总结,获得新知 思考 你能从四边形、五边形、六边形的内角和的
研究过程获得启发,发现多边形的内角和与边数的关系
吗?能证明你发现的结论吗?······归纳总结,梳理新知03 -3 =4 -3 =5 -3 =6 -3 =n -3 1233 -2 =14 -2 =25 -2 =3 6 -2 =4 n -2 ( n -2 )·180o180o360o 540o720o··················1 4408动脑思考,例题解析 例1 填空:
(1)十边形的内角和为 度.
(2)已知一个多边形的内角和为1 080°,则它的边数
为______.解:如图,四边形ABCD 中,
∠A +∠C =180°.
∵ ∠A +∠B +∠C +∠D
=(4 - 2)×180° =360°,
∴ ∠B +∠D
=360°-(∠A + ∠C) =360°- 180° =180°. 动脑思考,例题解析 例2 如果一个四边形的一组对角互补,那么另一
组对角有什么关系?如果四边形的一组对角互补,那么另一组对角也互补.(1)本节课学习了哪些主要内容?
(2)我们是怎样得到多边形内角和公式的?
(3)在探究多边形内角和公式中,连接对角线起到
什么作用?课堂小结 教科书习题11.3第1、2、4、5题.布置作业
的基础上,利用学习三角形的经验方法进一步研究
多边形的有关概念和性质.学习目标:
1.了解多边形的有关概念,感悟类比方法的价值.
2.探索并证明多边形内角和公式,体会化归思想和
从具体到抽象的研究问题方法.
3.运用多边形内角和公式解决简单问题.
学习重点:
多边形内角和公式的探索与证明过程.
课件说明创设情境,导入新知 问题 你能从图中想象出几个由一些线段围成的图
形吗?创设情境,导入新知 多边形的定义:
在平面内,由一些线段首尾顺次相接组成的封闭图
形叫做多边形.创设情境,导入新知 如图,从五边形ABCDE 的顶点A 出发共有几条对
角线?凸四边形创设情境,导入新知 观察 你能说出这两个图形的异同点吗?创设情境,导入新知 想一想 正方形的边、角有什么特点?各个角都相等,各条边都相等的多边形叫做正多边形. 回忆 长方形、正方形的内角和等于______.360° 创设情境,导入新知 思考 任意一个四边形的内角和是否也等于360° 呢?动手操作,探究新知 探究 你能利用三角形内角和定理证明你的结论
吗?证明:连接AC,
∠BAD +∠B +∠BCD +∠D
=(∠BAC +∠BCA +∠B)
+ (∠DAC +∠DCA +∠D),
= 180° + 180° = 360° .动手操作,探究新知 探究 你能利用三角形内角和定理证明你的结论
吗? 从四边形的一个顶点出发,
可以作_____条对角线,它们将
四边形分为 个三角形,
四边形的内角和等于
180°×____= °.122360动手操作,探究新知 探究 类比前面的过程,你能探索五边形的内角和
吗?六边形呢? 如图,从五边形的一个顶点
出发,可以作 条对角线,它
们将五边形分为____个三角形,
五边形的内角和等于
180°× = °.233540动手操作,探究新知 如图,从六边形的一个顶点出发,可以作_____条
对角线,它们将六边形分为_____个三角形,六边形的
内角和等于180°×____=_______°.344720C 从n 边形的一个顶点出发,可以作(n -3)条对角
线,它们将n 边形分为(n -2)个三角形,这(n -2)
个三角形的内角和就是n 边形的内角和,所以,n 边形
的内角和等于(n -2)×180°.归纳总结,获得新知 思考 你能从四边形、五边形、六边形的内角和的
研究过程获得启发,发现多边形的内角和与边数的关系
吗?能证明你发现的结论吗?······归纳总结,梳理新知03 -3 =4 -3 =5 -3 =6 -3 =n -3 1233 -2 =14 -2 =25 -2 =3 6 -2 =4 n -2 ( n -2 )·180o180o360o 540o720o··················1 4408动脑思考,例题解析 例1 填空:
(1)十边形的内角和为 度.
(2)已知一个多边形的内角和为1 080°,则它的边数
为______.解:如图,四边形ABCD 中,
∠A +∠C =180°.
∵ ∠A +∠B +∠C +∠D
=(4 - 2)×180° =360°,
∴ ∠B +∠D
=360°-(∠A + ∠C) =360°- 180° =180°. 动脑思考,例题解析 例2 如果一个四边形的一组对角互补,那么另一
组对角有什么关系?如果四边形的一组对角互补,那么另一组对角也互补.(1)本节课学习了哪些主要内容?
(2)我们是怎样得到多边形内角和公式的?
(3)在探究多边形内角和公式中,连接对角线起到
什么作用?课堂小结 教科书习题11.3第1、2、4、5题.布置作业
