3.1.2 第1课时 椭圆的几何性质 课件(共25张PPT)
文档属性
| 名称 | 3.1.2 第1课时 椭圆的几何性质 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 15.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 16:18:57 | ||
图片预览






文档简介
(共25张PPT)
3.1.2 椭圆的简单几何性质
第1课时 椭圆的几何性质
第三章 圆锥曲线的方程
问题引入
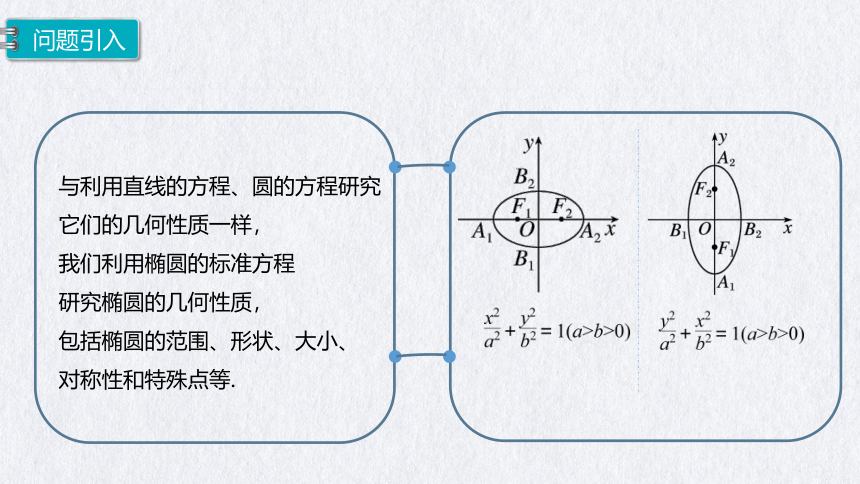
与利用直线的方程、圆的方程研究
它们的几何性质一样,
我们利用椭圆的标准方程
研究椭圆的几何性质,
包括椭圆的范围、形状、大小、
对称性和特殊点等.
新知探索
椭圆的简单几何性质
1. 对称性
对于椭圆=1(a>b>0)标准方程,把 x 换成-x,或把 y 换成- y,
或把 x、y 同时换成- x、 - y,方程都不变,
所以椭圆=1(a>b>0)是以 x 轴、y轴为对称轴的轴对称图形,
且是以原点为对称中心的中心对称图形,这个对称中心称为椭圆的中心.
新知探索
椭圆的简单几何性质
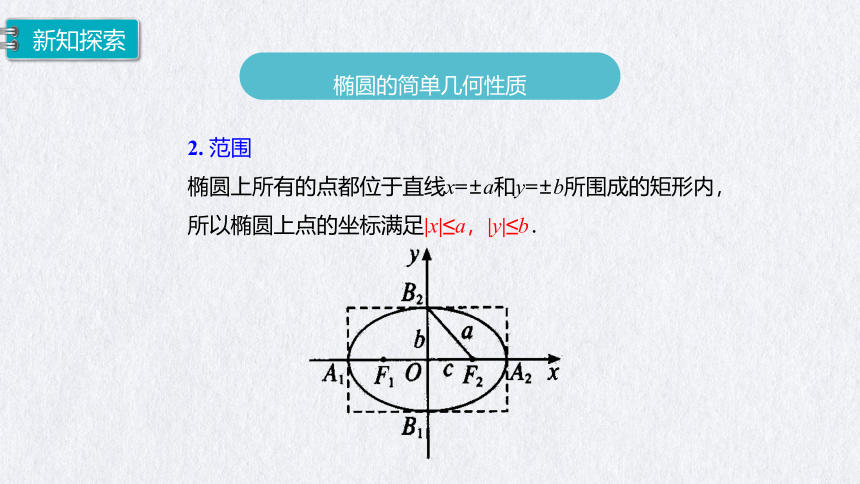
2. 范围
椭圆上所有的点都位于直线x=±a和y=±b所围成的矩形内,
所以椭圆上点的坐标满足|x|≤a,|y|≤b.
新知探索
椭圆的简单几何性质
3. 顶点
①椭圆的对称轴与椭圆的交点称为椭圆的顶点.
②椭圆=1(a>b>0)与坐标轴的四个交点即为椭圆的四个顶点,
坐标分别为A1(-a,0),A2(a,0),B1(0,-b),B2(0,b).
③线段A1A2,B1B2分别叫做椭圆的长轴和短轴,|A1A2|=2a,|B1B2|=2b.
a和b分别叫做椭圆的长半轴长和短半轴长.
新知探索
椭圆的简单几何性质
4.离心率
① 椭圆的焦距与长轴长度的比叫做椭圆的离心率,用 e 表示,记作e==.
② 因为 a>c>0,所以 e 的取值范围是 0<e<1.e 越接近1,则 c 就越接近 a,从而b=越小,因此椭圆越扁;反之,e 越接近于0,c 就越接近0,
从而 b 越接近于 a,这时椭圆就越接近于圆.当且仅当 a = b 时,c = 0,
这时两个焦点重合,图形变为圆,方程为 x2 + y2 = a2.
新知探索
椭圆的简单几何性质
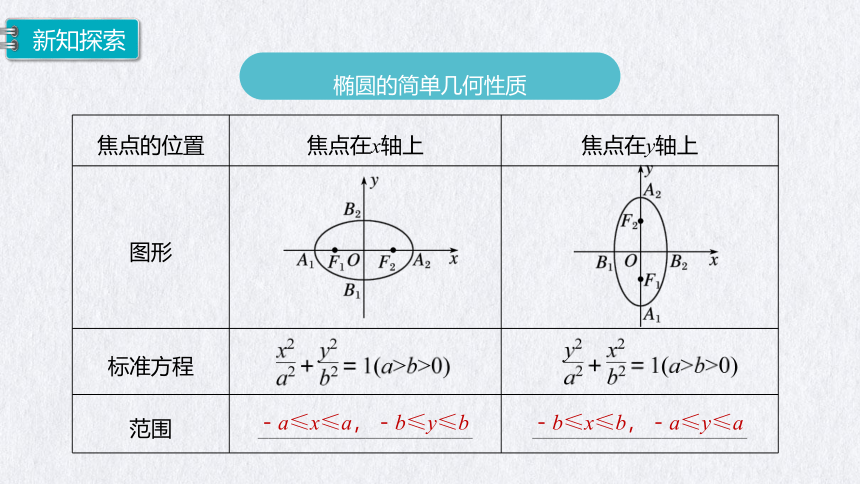
焦点的位置 焦点在x轴上 焦点在y轴上
图形
标准方程
范围 ____________________ ____________________
-a≤x≤a,-b≤y≤b
-b≤x≤b,-a≤y≤a
顶点 ______________________ ______________________ ______________________
______________________
轴长 短轴长= ,长轴长=____
焦点
焦距 |F1F2|=
对称性 对称轴: 对称中心:_____
离心率 e= ∈_____
A1(-a,0),A2(a,0),
B1(0,-b),B2(0,b)
A1(0,-a),A2(0,a),
B1(-b,0),B2(b,0)
2b
2a
x轴、y轴
原点
(0,1)
典例精析
题型一:由方程研究椭圆的几何性质
例1 求椭圆x2+4y2=16的长轴和短轴的长、离心率、焦点和顶点的坐标.
解 由已知,方程可化为+=1.
∴a=4,b=2,c=2.
∴长轴长为2a=8,短轴长为2b=4,
离心率e==,
焦点坐标为F1(-2,0),F2(2,0),
四个顶点坐标分别为A1(-4,0),A2(4,0),B1(0,-2),B2(0,2).
例2 设椭圆方程mx2+4y2=4m(m>0)的离心率为,试求椭圆的长轴长和短轴长、焦点坐标及顶点坐标.
典例精析
题型一:由方程研究椭圆的几何性质
解 椭圆方程可化为+=1.
(1)当0<m<4时,a=2,b=,c=,
∴e===,
∴m=3,∴b=,c=1,
∴椭圆的长轴长和短轴长分别是4,2,焦点坐标为F1(-1,0),F2(1,0),
顶点坐标为A1(-2,0),A2(2,0),B1(0,-),B2(0,).
(2)当m>4时,a=,b=2,c=,
∴e===,
∴m=,∴a=,c=,
∴椭圆的长轴长和短轴长分别是, 4,焦点坐标为F1(0, ),F2(0, ),
顶点坐标为A1(0, ),A2(0, ),B1(-2,0),B2(2,).
例2 设椭圆方程mx2+4y2=4m(m>0)的离心率为,试求椭圆的长轴长和短轴长、焦点坐标及顶点坐标.
典例精析
题型一:由方程研究椭圆的几何性质
典例精析
题型二:由几何性质求方程
例3 根据下列条件,求中心在原点,对称轴在坐标轴上的椭圆方程.
(1)焦点在x轴上,一个焦点与短轴的两端点连线互相垂直,且半焦距为6;
(2)与椭圆+=1有相同的焦点,且离心率e=;
(3)以直线3x+4y-12=0与两坐标轴的交点为一个顶点和一个焦点.
解 (1)依题意有b=c=6,
∴a2=b2+c2=72.
∴所求的椭圆方程为+=1.
(2)∵c==,
∴所求椭圆的焦点为(-,0),(,0).
设所求椭圆的方程为+=1(a>b>0).
∵e=,c=,∴a=5,b2=a2-c2=20.
∴所求椭圆的方程为+=1.
典例精析
题型二:由几何性质求方程
例3 根据下列条件,求中心在原点,对称轴在坐标轴上的椭圆方程.
(3)以直线3x+4y-12=0与两坐标轴的交点为一个顶点和一个焦点.
(3)直线3x+4y-12=0与两坐标轴的交点分别为(0,3),(4,0).
①若以(4,0)为一个焦点,则c=4,b=3,a=5.
∴椭圆的标准方程为+=1.
②若以(0,3)为一个焦点,则c=3,b=4,a=5.
∴椭圆的标准方程为+=1.
综上,所求椭圆的方程为+=1或+=1.
典例精析
题型三:求椭圆的离心率
例4 (1)设椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为_____.
解 方法一 由题意可设|PF2|=m,
结合条件可知|PF1|=2m,|F1F2|=m,
故离心率e=====.
方法二 由PF2⊥F1F2可知P点的横坐标为c,
将x=c代入椭圆方程可解得y=±,
所以|PF2|=.
又由∠PF1F2=30°可得|F1F2|=|PF2|,
故2c=·
变形可得(a2-c2)=2ac,
等式两边同除以a2,得(1-e2)=2e,
解得e=或e=-(舍去).
典例精析
题型三:求椭圆的离心率
(2)已知F1,F2分别是椭圆+=1(a>b>0)的左、右焦点,P是以F1F2为直径的圆与该椭圆的一个交点,且∠PF1F2=2∠PF2F1,则这个椭圆的离心率是________.
解 由题意知△PF1F2为直角三角形,
且∠F1PF2=90°,∠PF1F2=60°,|F1F2|=2c,
则|PF1|=c,|PF2|=c,由椭圆的定义知,
|PF1|+|PF2|=2a,即c+c=2a,
得离心率e==-1.
-1
典例精析
题型三:求椭圆的离心率
(3)若椭圆+=1(a>b>0)上存在一点M,使得∠F1MF2=90°(F1,F2分别为椭圆的左、右焦点),则椭圆的离心率e的取值范围为________.
解 方法一:设点M的坐标是(x0,y0),则|x0|∵F1(-c,0),F2(c,0),
∴=(-c-x0,-y0),=(c-x0,-y0).
∵∠F1MF2=90°,∴·=0,∴x02+y02=c2.
又y02=b2-x02,∴x02+y02=b2+x02∈[b2,a2),
即c2∈[b2,a2),∴c2≥b2=a2-c2,∴≥,∴e≥或e≤-,
又0典例精析
题型三:求椭圆的离心率
(3)若椭圆+=1(a>b>0)上存在一点M,使得∠F1MF2=90°(F1,F2分别为椭圆的左、右焦点),则椭圆的离心率e的取值范围为________.
方法二:设点M的坐标是(x0,y0),则|x0|由,消去y0,得x02=.
∵0≤x02由①得c2≥b2,即c2≥a2-c2,
∴a2≤2c2,∴e2=≥.
又0由②得c2-b2综上所述,
椭圆的离心率e的取值范围是[,1).
典例精析
题型三:求椭圆的离心率
(3)若椭圆+=1(a>b>0)上存在一点M,使得∠F1MF2=90°(F1,F2分别为椭圆的左、右焦点),则椭圆的离心率e的取值范围为________.
方法三:设椭圆与y轴的一个交点为P,连接PF1,PF2.
∵椭圆上存在一点M,使∠F1MF2=90°,
∴∠F1PF2≥90°,则c≥b,
∴c2≥b2=a2-c2,∴≥,∴e≥或e≤-,
又0跟踪练习
则a=6,∴b2=a2-c2=27,
√
跟踪练习
2.若椭圆的两个焦点与短轴的一个端点构成一个正三角形,则该椭圆的离心率为
√
解 不妨设椭圆的左、右焦点分别为F1,F2,B为椭圆的上顶点.
依题意可知,△BF1F2是正三角形.
∵在Rt△OBF2中,|OF2|=c,
|BF2|=a,∠OF2B=60°,
跟踪练习
跟踪练习
跟踪练习
4.如图所示,圆柱形玻璃杯中的水液面呈椭圆形状,则该椭圆的离心率为( )
A. B. C. D.
解 椭圆的短轴长为圆柱的直径,椭圆的长轴、圆柱底面的直径和母线三者组成一个直角三角形,且长轴与母线的夹角为30°,b=r,a==2r,
所以c==r,e==.
D
课堂小结
本
课
结
束
3.1.2 椭圆的简单几何性质
第1课时 椭圆的几何性质
第三章 圆锥曲线的方程
问题引入
与利用直线的方程、圆的方程研究
它们的几何性质一样,
我们利用椭圆的标准方程
研究椭圆的几何性质,
包括椭圆的范围、形状、大小、
对称性和特殊点等.
新知探索
椭圆的简单几何性质
1. 对称性
对于椭圆=1(a>b>0)标准方程,把 x 换成-x,或把 y 换成- y,
或把 x、y 同时换成- x、 - y,方程都不变,
所以椭圆=1(a>b>0)是以 x 轴、y轴为对称轴的轴对称图形,
且是以原点为对称中心的中心对称图形,这个对称中心称为椭圆的中心.
新知探索
椭圆的简单几何性质
2. 范围
椭圆上所有的点都位于直线x=±a和y=±b所围成的矩形内,
所以椭圆上点的坐标满足|x|≤a,|y|≤b.
新知探索
椭圆的简单几何性质
3. 顶点
①椭圆的对称轴与椭圆的交点称为椭圆的顶点.
②椭圆=1(a>b>0)与坐标轴的四个交点即为椭圆的四个顶点,
坐标分别为A1(-a,0),A2(a,0),B1(0,-b),B2(0,b).
③线段A1A2,B1B2分别叫做椭圆的长轴和短轴,|A1A2|=2a,|B1B2|=2b.
a和b分别叫做椭圆的长半轴长和短半轴长.
新知探索
椭圆的简单几何性质
4.离心率
① 椭圆的焦距与长轴长度的比叫做椭圆的离心率,用 e 表示,记作e==.
② 因为 a>c>0,所以 e 的取值范围是 0<e<1.e 越接近1,则 c 就越接近 a,从而b=越小,因此椭圆越扁;反之,e 越接近于0,c 就越接近0,
从而 b 越接近于 a,这时椭圆就越接近于圆.当且仅当 a = b 时,c = 0,
这时两个焦点重合,图形变为圆,方程为 x2 + y2 = a2.
新知探索
椭圆的简单几何性质
焦点的位置 焦点在x轴上 焦点在y轴上
图形
标准方程
范围 ____________________ ____________________
-a≤x≤a,-b≤y≤b
-b≤x≤b,-a≤y≤a
顶点 ______________________ ______________________ ______________________
______________________
轴长 短轴长= ,长轴长=____
焦点
焦距 |F1F2|=
对称性 对称轴: 对称中心:_____
离心率 e= ∈_____
A1(-a,0),A2(a,0),
B1(0,-b),B2(0,b)
A1(0,-a),A2(0,a),
B1(-b,0),B2(b,0)
2b
2a
x轴、y轴
原点
(0,1)
典例精析
题型一:由方程研究椭圆的几何性质
例1 求椭圆x2+4y2=16的长轴和短轴的长、离心率、焦点和顶点的坐标.
解 由已知,方程可化为+=1.
∴a=4,b=2,c=2.
∴长轴长为2a=8,短轴长为2b=4,
离心率e==,
焦点坐标为F1(-2,0),F2(2,0),
四个顶点坐标分别为A1(-4,0),A2(4,0),B1(0,-2),B2(0,2).
例2 设椭圆方程mx2+4y2=4m(m>0)的离心率为,试求椭圆的长轴长和短轴长、焦点坐标及顶点坐标.
典例精析
题型一:由方程研究椭圆的几何性质
解 椭圆方程可化为+=1.
(1)当0<m<4时,a=2,b=,c=,
∴e===,
∴m=3,∴b=,c=1,
∴椭圆的长轴长和短轴长分别是4,2,焦点坐标为F1(-1,0),F2(1,0),
顶点坐标为A1(-2,0),A2(2,0),B1(0,-),B2(0,).
(2)当m>4时,a=,b=2,c=,
∴e===,
∴m=,∴a=,c=,
∴椭圆的长轴长和短轴长分别是, 4,焦点坐标为F1(0, ),F2(0, ),
顶点坐标为A1(0, ),A2(0, ),B1(-2,0),B2(2,).
例2 设椭圆方程mx2+4y2=4m(m>0)的离心率为,试求椭圆的长轴长和短轴长、焦点坐标及顶点坐标.
典例精析
题型一:由方程研究椭圆的几何性质
典例精析
题型二:由几何性质求方程
例3 根据下列条件,求中心在原点,对称轴在坐标轴上的椭圆方程.
(1)焦点在x轴上,一个焦点与短轴的两端点连线互相垂直,且半焦距为6;
(2)与椭圆+=1有相同的焦点,且离心率e=;
(3)以直线3x+4y-12=0与两坐标轴的交点为一个顶点和一个焦点.
解 (1)依题意有b=c=6,
∴a2=b2+c2=72.
∴所求的椭圆方程为+=1.
(2)∵c==,
∴所求椭圆的焦点为(-,0),(,0).
设所求椭圆的方程为+=1(a>b>0).
∵e=,c=,∴a=5,b2=a2-c2=20.
∴所求椭圆的方程为+=1.
典例精析
题型二:由几何性质求方程
例3 根据下列条件,求中心在原点,对称轴在坐标轴上的椭圆方程.
(3)以直线3x+4y-12=0与两坐标轴的交点为一个顶点和一个焦点.
(3)直线3x+4y-12=0与两坐标轴的交点分别为(0,3),(4,0).
①若以(4,0)为一个焦点,则c=4,b=3,a=5.
∴椭圆的标准方程为+=1.
②若以(0,3)为一个焦点,则c=3,b=4,a=5.
∴椭圆的标准方程为+=1.
综上,所求椭圆的方程为+=1或+=1.
典例精析
题型三:求椭圆的离心率
例4 (1)设椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为_____.
解 方法一 由题意可设|PF2|=m,
结合条件可知|PF1|=2m,|F1F2|=m,
故离心率e=====.
方法二 由PF2⊥F1F2可知P点的横坐标为c,
将x=c代入椭圆方程可解得y=±,
所以|PF2|=.
又由∠PF1F2=30°可得|F1F2|=|PF2|,
故2c=·
变形可得(a2-c2)=2ac,
等式两边同除以a2,得(1-e2)=2e,
解得e=或e=-(舍去).
典例精析
题型三:求椭圆的离心率
(2)已知F1,F2分别是椭圆+=1(a>b>0)的左、右焦点,P是以F1F2为直径的圆与该椭圆的一个交点,且∠PF1F2=2∠PF2F1,则这个椭圆的离心率是________.
解 由题意知△PF1F2为直角三角形,
且∠F1PF2=90°,∠PF1F2=60°,|F1F2|=2c,
则|PF1|=c,|PF2|=c,由椭圆的定义知,
|PF1|+|PF2|=2a,即c+c=2a,
得离心率e==-1.
-1
典例精析
题型三:求椭圆的离心率
(3)若椭圆+=1(a>b>0)上存在一点M,使得∠F1MF2=90°(F1,F2分别为椭圆的左、右焦点),则椭圆的离心率e的取值范围为________.
解 方法一:设点M的坐标是(x0,y0),则|x0|
∴=(-c-x0,-y0),=(c-x0,-y0).
∵∠F1MF2=90°,∴·=0,∴x02+y02=c2.
又y02=b2-x02,∴x02+y02=b2+x02∈[b2,a2),
即c2∈[b2,a2),∴c2≥b2=a2-c2,∴≥,∴e≥或e≤-,
又0
题型三:求椭圆的离心率
(3)若椭圆+=1(a>b>0)上存在一点M,使得∠F1MF2=90°(F1,F2分别为椭圆的左、右焦点),则椭圆的离心率e的取值范围为________.
方法二:设点M的坐标是(x0,y0),则|x0|
∵0≤x02
∴a2≤2c2,∴e2=≥.
又0
椭圆的离心率e的取值范围是[,1).
典例精析
题型三:求椭圆的离心率
(3)若椭圆+=1(a>b>0)上存在一点M,使得∠F1MF2=90°(F1,F2分别为椭圆的左、右焦点),则椭圆的离心率e的取值范围为________.
方法三:设椭圆与y轴的一个交点为P,连接PF1,PF2.
∵椭圆上存在一点M,使∠F1MF2=90°,
∴∠F1PF2≥90°,则c≥b,
∴c2≥b2=a2-c2,∴≥,∴e≥或e≤-,
又0
则a=6,∴b2=a2-c2=27,
√
跟踪练习
2.若椭圆的两个焦点与短轴的一个端点构成一个正三角形,则该椭圆的离心率为
√
解 不妨设椭圆的左、右焦点分别为F1,F2,B为椭圆的上顶点.
依题意可知,△BF1F2是正三角形.
∵在Rt△OBF2中,|OF2|=c,
|BF2|=a,∠OF2B=60°,
跟踪练习
跟踪练习
跟踪练习
4.如图所示,圆柱形玻璃杯中的水液面呈椭圆形状,则该椭圆的离心率为( )
A. B. C. D.
解 椭圆的短轴长为圆柱的直径,椭圆的长轴、圆柱底面的直径和母线三者组成一个直角三角形,且长轴与母线的夹角为30°,b=r,a==2r,
所以c==r,e==.
D
课堂小结
本
课
结
束
