3.1.2 第2课时 椭圆的标准方程及性质的应用 课件(共22张PPT)
文档属性
| 名称 | 3.1.2 第2课时 椭圆的标准方程及性质的应用 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
第三章 圆锥曲线的方程
3.1.2 椭圆的简单几何性质
第2课时 椭圆的标准方程及性质的应用
问题引入
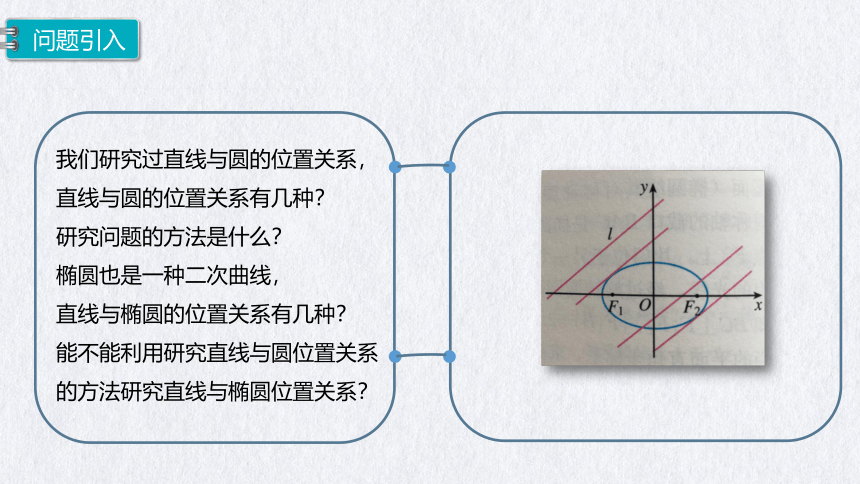
我们研究过直线与圆的位置关系,
直线与圆的位置关系有几种?
研究问题的方法是什么?
椭圆也是一种二次曲线,
直线与椭圆的位置关系有几种?
能不能利用研究直线与圆位置关系的方法研究直线与椭圆位置关系?
新知探索
直线与椭圆的位置关系
通过解直线方程与椭圆方程组成的方程组,对解的个数进行讨论.
通常消去方程组中的一个变量,得到关于另一变量的一元二次方程.
(1)Δ>0 直线与椭圆相交 有两个不同的公共点;
(2)Δ=0 直线与椭圆相切 有且只有一个公共点;
(3)Δ<0 直线与椭圆相离 无公共点.
新知探索
弦长问题
通常将直线方程与椭圆方程联立,得到关于x(或y)的一元二次方程,
然后利用根与系数的关系求弦长,从而绕过求直线与椭圆的交点坐标.
若直线y=kx+b与椭圆相交于A(x1,y1),B(x2,y2)两点,
则|AB|=|x1-x2|= ·,
或|AB|=·|y1-y2|= · .
新知探索
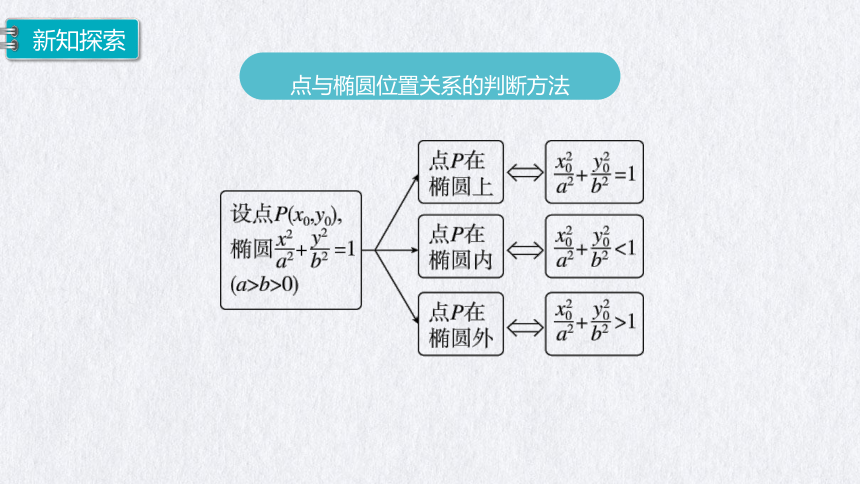
点与椭圆位置关系的判断方法
新知探索
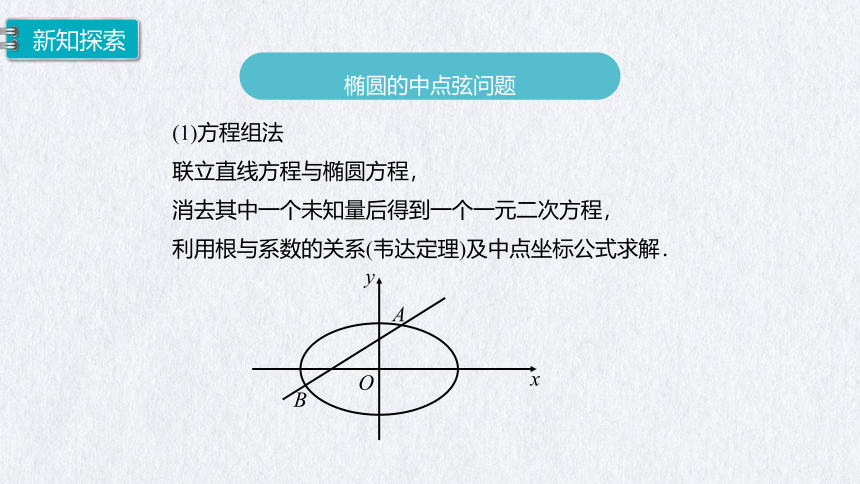
椭圆的中点弦问题
(1)方程组法
联立直线方程与椭圆方程,
消去其中一个未知量后得到一个一元二次方程,
利用根与系数的关系(韦达定理)及中点坐标公式求解.
y
A
B
O
x
新知探索
椭圆的中点弦问题
(2)点差法
设直线与椭圆+=1(m>0,n>0,m≠n)的交点(弦的端点)
坐标为A(x1,y1),B(x2,y2),弦AB的中点(x0,y0),
将这两点代入椭圆的方程并对所得两式作差,
得到kAB==-·=-·.
y
A
B
O
x
典例精析
题型一:直线与椭圆的位置关系
例1 已知直线y=x+m和椭圆4x2+y2=1.当直线与椭圆有公共点时,
求实数m的取值范围.
解 由方程组,
消去y,整理得5x2+2mx+m2-1=0.
Δ=4m2-20(m2-1)=20-16m2.
由Δ≥0,得20-16m2≥0,解得-≤m≤.
例2 若直线y=kx+1与焦点在x轴上的椭圆+=1总有公共点,求m的取值范围.
典例精析
题型一:直线与椭圆的位置关系
解 方法一:由,消去y,
得(m+5k2)x2+10kx+5(1-m)=0.
∵直线与椭圆总有公共点,
∴Δ=100k2-20(m+5k2)(1-m)≥0.
又∵m>0,∴m≥1-5k2.
而1-5k2的最大值为1,则m≥1.
又m<5,则1≤m<5.
方法二:∵直线y=kx+1恒过定点(0,1),
∴若直线与椭圆总有公共点,
则点(0,1)不在椭圆外部.
∴+≤1,又∵m>0,∴m≥1.
又椭圆焦点在x轴上,∴m<5.
∴1≤m<5.
典例精析
题型一:直线与椭圆的位置关系
例3 已知直线l:x+y=6,P为椭圆+=1上一点,求P到l的最大距离.
y
O
x
解 设直线x+y=m与椭圆相切,
由,消去y,
得5x2-8mx+4m2-20=0.
令Δ=(-8m)2-4×5×(4m2-20)=0,
得m=5或m=-5.
∴所求最大距离即为直线x+y=-5与直线l间的距离,
∴最大距离为=.
例4 已知A(6,0),B(0,6),C为椭圆+=1上一点,求△ABC面积的最小值.
典例精析
题型一:直线与椭圆的位置关系
解 由题意知直线AB的方程为x+y=6,
设直线x+y=m与椭圆相切,
联立方程,消去y,
得5x2-8mx+4m2-20=0.
由Δ=0,得m=5或-5.
∴C到直线AB的最小距离为.
∴S△ABC的最小值为×|AB|=3.
典例精析
题型二:弦长问题
例5 (1)已知斜率为1的直线l过椭圆+y2=1的右焦点交椭圆于A,B两点,求弦AB的长.
解 设直线l与椭圆的交点为A(x1,y1),B(x2,y2),
且椭圆方程中a2=4,b2=1,c2=3,
所以右焦点的坐标为(,0).
所以直线l的方程为y=x-.
将上式代入+y2=1,
整理可得5x2-8x+8=0,
则Δ=(-8)2-4×5×8=32>0,
故x1+x2=,x1x2=.
所以|AB|=|x1-x2|
=×
= .
跟踪练习
典例精析
题型二:弦长问题
(2)已知椭圆4x2+y2=1及直线y=x+m,求被椭圆截得的最长弦所在的直线方程.
解 设直线与椭圆交于两点A(x1,y1),B(x2,y2).
则x1,x2是方程5x2+2mx+m2-1=0的两根.
由Δ>0,得4m2-20(m2-1)>0,解得m2<.
由韦达定理,得x1+x2=-,x1·x2=.
∴弦长= ·
=
=≤,
当且仅当m=0时取等号,
此时直线方程为y=x.
例6 已知一直线与椭圆4x2+9y2=36相交于A,B两点,弦AB的中点坐标为M(1,1),求直线AB的方程.
跟踪练习
典例精析
题型三:中点弦问题
解 方法一:设通过点M(1,1)的
直线AB的方程为y=k(x-1)+1,
代入椭圆方程,整理得
(9k2+4)x2+18k(1-k)x+9(1-k)2-36=0.
则Δ=32k2+8k+12=32+>0.
设A,B的横坐标分别为x1,x2,
则==1,解得k=-.
故AB的方程为y=-(x-1)+1,
即4x+9y-13=0.
方法二:设A(x1,y1),B(x2,y2),
则
两式相减得
4(x2-x1)(x2+x1)+9(y2-y1)(y2+y1)=0.
∵M为AB中点,∴x1+x2=2,y1+y2=2.
∴4(x2-x1)+9(y2-y1)=0.
例6 已知一直线与椭圆4x2+9y2=36相交于A,B两点,弦AB的中点坐标为M(1,1),求直线AB的方程.
跟踪练习
典例精析
题型三:中点弦问题
∴=-,即kAB=-.
由点斜式得AB的方程为 y-1=-(x-1),
即4x+9y-13=0.
跟踪练习
1.直线l:kx-y-k=0与椭圆+=1的位置关系是( )
A.相交 B.相离
C.相切 D.不确定
解 ∵kx-y-k=0,∴y=k(x-1),
即直线过定点(1,0),
而(1,0)点在+=1的内部,
故直线l与椭圆+=1相交.
A
跟踪练习
2.若直线y=kx+2与椭圆+=1相切,则斜率k的值是( )
A. B.-
C.± D.±
C
解 把y=kx+2代入+=1,
得(3k2+2)x2+12kx+6=0,
因为直线与椭圆相切,
所以Δ=(12k)2-4(3k2+2)×6=0,解得k=±.
跟踪练习
3.已知椭圆+y2=1,求过点P(, )且被 P 平分的弦所在的直线方程.
解 法一:设所求直线的斜率为k,则直线方程为y-=k(x-).
代入椭圆方程,并整理得(1+2k2)x2-(2k2-2k)x+k2-k-=0
由韦达定理得x1+x2=.
∵P 是弦中点,∴x1+x2 = 1.故得k=- .
所以所求直线方程为 2x+4y- 3=0.
跟踪练习
解 法二:设过P(, )的直线与椭圆交于A(x1, y1)、B(x2, y2) ,
则由题意得,
两式相减得
即=-,即直线的斜率为-.
所求直线方程为2x+4y- 3=0 .
3.已知椭圆+y2=1,求过点P(, )且被 P 平分的弦所在的直线方程.
4.已知椭圆ax2+by2=1与直线x+y-1=0相交于A,B两点,C是AB的中点.
若AB=2,OC的斜率为,求椭圆的方程.
跟踪练习
解 设A(x1,y1),B(x2,y2),
代入椭圆方程并作差得a(x1+x2)(x1-x2)+b(y1+y2)(y1-y2)=0.
=-1,=kOC=,代入上式可得b=a.
由|AB|=|x2-x1|=|x2-x1|=2,
其中x1,x2是方程(a+b)x2-2bx+b-1=0的两根,
故|x2-x1|2=(x1+x2)2-4x1x2=4.
将b=a代入得a=,所以b=.所以椭圆方程是+=1.
课堂小结
本
课
结
束
第三章 圆锥曲线的方程
3.1.2 椭圆的简单几何性质
第2课时 椭圆的标准方程及性质的应用
问题引入
我们研究过直线与圆的位置关系,
直线与圆的位置关系有几种?
研究问题的方法是什么?
椭圆也是一种二次曲线,
直线与椭圆的位置关系有几种?
能不能利用研究直线与圆位置关系的方法研究直线与椭圆位置关系?
新知探索
直线与椭圆的位置关系
通过解直线方程与椭圆方程组成的方程组,对解的个数进行讨论.
通常消去方程组中的一个变量,得到关于另一变量的一元二次方程.
(1)Δ>0 直线与椭圆相交 有两个不同的公共点;
(2)Δ=0 直线与椭圆相切 有且只有一个公共点;
(3)Δ<0 直线与椭圆相离 无公共点.
新知探索
弦长问题
通常将直线方程与椭圆方程联立,得到关于x(或y)的一元二次方程,
然后利用根与系数的关系求弦长,从而绕过求直线与椭圆的交点坐标.
若直线y=kx+b与椭圆相交于A(x1,y1),B(x2,y2)两点,
则|AB|=|x1-x2|= ·,
或|AB|=·|y1-y2|= · .
新知探索
点与椭圆位置关系的判断方法
新知探索
椭圆的中点弦问题
(1)方程组法
联立直线方程与椭圆方程,
消去其中一个未知量后得到一个一元二次方程,
利用根与系数的关系(韦达定理)及中点坐标公式求解.
y
A
B
O
x
新知探索
椭圆的中点弦问题
(2)点差法
设直线与椭圆+=1(m>0,n>0,m≠n)的交点(弦的端点)
坐标为A(x1,y1),B(x2,y2),弦AB的中点(x0,y0),
将这两点代入椭圆的方程并对所得两式作差,
得到kAB==-·=-·.
y
A
B
O
x
典例精析
题型一:直线与椭圆的位置关系
例1 已知直线y=x+m和椭圆4x2+y2=1.当直线与椭圆有公共点时,
求实数m的取值范围.
解 由方程组,
消去y,整理得5x2+2mx+m2-1=0.
Δ=4m2-20(m2-1)=20-16m2.
由Δ≥0,得20-16m2≥0,解得-≤m≤.
例2 若直线y=kx+1与焦点在x轴上的椭圆+=1总有公共点,求m的取值范围.
典例精析
题型一:直线与椭圆的位置关系
解 方法一:由,消去y,
得(m+5k2)x2+10kx+5(1-m)=0.
∵直线与椭圆总有公共点,
∴Δ=100k2-20(m+5k2)(1-m)≥0.
又∵m>0,∴m≥1-5k2.
而1-5k2的最大值为1,则m≥1.
又m<5,则1≤m<5.
方法二:∵直线y=kx+1恒过定点(0,1),
∴若直线与椭圆总有公共点,
则点(0,1)不在椭圆外部.
∴+≤1,又∵m>0,∴m≥1.
又椭圆焦点在x轴上,∴m<5.
∴1≤m<5.
典例精析
题型一:直线与椭圆的位置关系
例3 已知直线l:x+y=6,P为椭圆+=1上一点,求P到l的最大距离.
y
O
x
解 设直线x+y=m与椭圆相切,
由,消去y,
得5x2-8mx+4m2-20=0.
令Δ=(-8m)2-4×5×(4m2-20)=0,
得m=5或m=-5.
∴所求最大距离即为直线x+y=-5与直线l间的距离,
∴最大距离为=.
例4 已知A(6,0),B(0,6),C为椭圆+=1上一点,求△ABC面积的最小值.
典例精析
题型一:直线与椭圆的位置关系
解 由题意知直线AB的方程为x+y=6,
设直线x+y=m与椭圆相切,
联立方程,消去y,
得5x2-8mx+4m2-20=0.
由Δ=0,得m=5或-5.
∴C到直线AB的最小距离为.
∴S△ABC的最小值为×|AB|=3.
典例精析
题型二:弦长问题
例5 (1)已知斜率为1的直线l过椭圆+y2=1的右焦点交椭圆于A,B两点,求弦AB的长.
解 设直线l与椭圆的交点为A(x1,y1),B(x2,y2),
且椭圆方程中a2=4,b2=1,c2=3,
所以右焦点的坐标为(,0).
所以直线l的方程为y=x-.
将上式代入+y2=1,
整理可得5x2-8x+8=0,
则Δ=(-8)2-4×5×8=32>0,
故x1+x2=,x1x2=.
所以|AB|=|x1-x2|
=×
= .
跟踪练习
典例精析
题型二:弦长问题
(2)已知椭圆4x2+y2=1及直线y=x+m,求被椭圆截得的最长弦所在的直线方程.
解 设直线与椭圆交于两点A(x1,y1),B(x2,y2).
则x1,x2是方程5x2+2mx+m2-1=0的两根.
由Δ>0,得4m2-20(m2-1)>0,解得m2<.
由韦达定理,得x1+x2=-,x1·x2=.
∴弦长= ·
=
=≤,
当且仅当m=0时取等号,
此时直线方程为y=x.
例6 已知一直线与椭圆4x2+9y2=36相交于A,B两点,弦AB的中点坐标为M(1,1),求直线AB的方程.
跟踪练习
典例精析
题型三:中点弦问题
解 方法一:设通过点M(1,1)的
直线AB的方程为y=k(x-1)+1,
代入椭圆方程,整理得
(9k2+4)x2+18k(1-k)x+9(1-k)2-36=0.
则Δ=32k2+8k+12=32+>0.
设A,B的横坐标分别为x1,x2,
则==1,解得k=-.
故AB的方程为y=-(x-1)+1,
即4x+9y-13=0.
方法二:设A(x1,y1),B(x2,y2),
则
两式相减得
4(x2-x1)(x2+x1)+9(y2-y1)(y2+y1)=0.
∵M为AB中点,∴x1+x2=2,y1+y2=2.
∴4(x2-x1)+9(y2-y1)=0.
例6 已知一直线与椭圆4x2+9y2=36相交于A,B两点,弦AB的中点坐标为M(1,1),求直线AB的方程.
跟踪练习
典例精析
题型三:中点弦问题
∴=-,即kAB=-.
由点斜式得AB的方程为 y-1=-(x-1),
即4x+9y-13=0.
跟踪练习
1.直线l:kx-y-k=0与椭圆+=1的位置关系是( )
A.相交 B.相离
C.相切 D.不确定
解 ∵kx-y-k=0,∴y=k(x-1),
即直线过定点(1,0),
而(1,0)点在+=1的内部,
故直线l与椭圆+=1相交.
A
跟踪练习
2.若直线y=kx+2与椭圆+=1相切,则斜率k的值是( )
A. B.-
C.± D.±
C
解 把y=kx+2代入+=1,
得(3k2+2)x2+12kx+6=0,
因为直线与椭圆相切,
所以Δ=(12k)2-4(3k2+2)×6=0,解得k=±.
跟踪练习
3.已知椭圆+y2=1,求过点P(, )且被 P 平分的弦所在的直线方程.
解 法一:设所求直线的斜率为k,则直线方程为y-=k(x-).
代入椭圆方程,并整理得(1+2k2)x2-(2k2-2k)x+k2-k-=0
由韦达定理得x1+x2=.
∵P 是弦中点,∴x1+x2 = 1.故得k=- .
所以所求直线方程为 2x+4y- 3=0.
跟踪练习
解 法二:设过P(, )的直线与椭圆交于A(x1, y1)、B(x2, y2) ,
则由题意得,
两式相减得
即=-,即直线的斜率为-.
所求直线方程为2x+4y- 3=0 .
3.已知椭圆+y2=1,求过点P(, )且被 P 平分的弦所在的直线方程.
4.已知椭圆ax2+by2=1与直线x+y-1=0相交于A,B两点,C是AB的中点.
若AB=2,OC的斜率为,求椭圆的方程.
跟踪练习
解 设A(x1,y1),B(x2,y2),
代入椭圆方程并作差得a(x1+x2)(x1-x2)+b(y1+y2)(y1-y2)=0.
=-1,=kOC=,代入上式可得b=a.
由|AB|=|x2-x1|=|x2-x1|=2,
其中x1,x2是方程(a+b)x2-2bx+b-1=0的两根,
故|x2-x1|2=(x1+x2)2-4x1x2=4.
将b=a代入得a=,所以b=.所以椭圆方程是+=1.
课堂小结
本
课
结
束
