3.2.1 第2课时 双曲线及其标准方程的应用 课件(共23张PPT)
文档属性
| 名称 | 3.2.1 第2课时 双曲线及其标准方程的应用 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 16:49:24 | ||
图片预览








文档简介
(共23张PPT)
第三章 圆锥曲线的方程
3.2.1 双曲线及其标准方程
第2课时 双曲线及其标准方程的应用
文字语言 平面内与两个定点F1,F2的距离的__________等于非零
常数(小于|F1F2|)的点的轨迹.
符号语言 ||PF1|-|PF2||=常数(常数<|F1F2|)
焦点 定点__________
焦距 ________的距离
差的绝对值
F1,F2
两焦点间
复习回顾
复习回顾
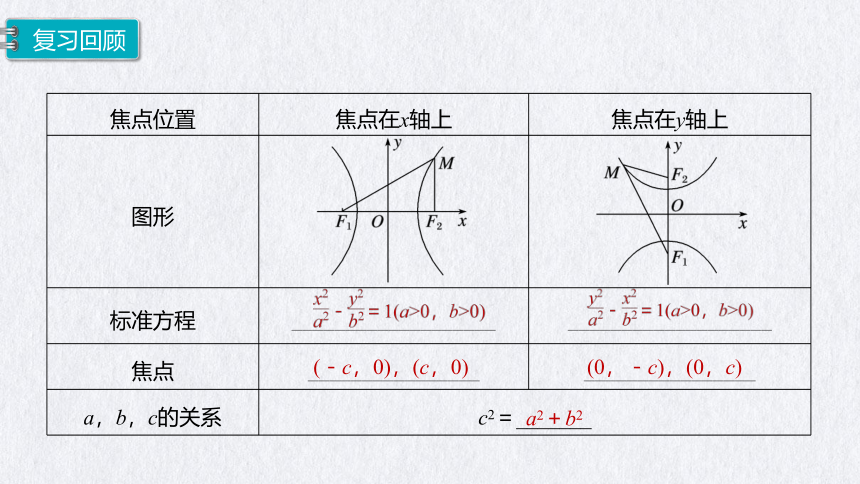
焦点位置 焦点在x轴上 焦点在y轴上
图形
标准方程 ___________________ ___________________
焦点 ________________ ________________
a,b,c的关系 c2=_______
(-c,0),(c,0)
(0,-c),(0,c)
a2+b2
典例精析
题型一:双曲线定义的应用
例1 如图,若F1,F2是双曲线-=1的两个焦点.
(1)若双曲线上一点P到它的一个焦点的距离等于16,求点P到另一个焦点的距离;
(2)若P是双曲线左支上的点,且|PF1|·|PF2|=32,试求△F1PF2的面积.
解 双曲线的标准方程为-=1,
故a=3,b=4,c=5.
(1)由双曲线的定义得||PF1|-|PF2||=2a=6,
又双曲线上一点P到它的一个焦点的距离等于16,
假设点P到另一个焦点的距离等于x,
则|16-x|=6,解得x=10或x=22.
故点P到另一个焦点的距离为10或22.
典例精析
题型一:双曲线定义的应用
例1 如图,若F1,F2是双曲线-=1的两个焦点.
(1)若双曲线上一点P到它的一个焦点的距离等于16,求点P到另一个焦点的距离;
(2)若P是双曲线左支上的点,且|PF1|·|PF2|=32,试求△F1PF2的面积.
(2)将||PF1|-|PF2|| =2a=6,两边平方得|PF1|2+|PF2|2-2|PF1|·|PF2|=36,
∴|PF1|2+|PF2|2=36+2|PF1|·|PF2|=36+2×32=100.
在△F1PF2中,由余弦定理得
cos ∠F1PF2==0,
∴∠F1PF2=90°,
∴S△F1PF2=|PF1|·|PF2|=×32=16.
典例精析
题型一:双曲线定义的应用
例2 △ABC中,A(-5,0),B(5,0),点C在双曲线-=1上,则=( )
A. B.± C.- D.±
解 在△ABC中,由正弦定理得==.
又∵|BC|-|AC|=±8,∴=±=±.
D
典例精析
题型二:与双曲线有关的轨迹问题
例3 已知两圆C1:(x+4)2+y2=2,C2:(x-4)2+y2=2,动圆M与圆C1外切,与圆C2内切,则动圆圆心M的轨迹方程为 .
解 设动圆圆心M(x,y),半径为r,
因为圆M与圆C1:(x+4)2+y2=2外切,与圆C2:(x-4)2+y2=2内切,
所以|MC1|=r+,|MC2|=r-,|MC1|-|MC2|=2<8.
由双曲线的定义知点M的轨迹
是以C1,C2为焦点的双曲线的右支,且a=,c=4,
故动圆圆心M的轨迹方程为=1(x≥).
=1(x≥)
典例精析
题型二:与双曲线有关的轨迹问题
例4 如图,在△ABC中,已知|AB|=4,且三内角A,B,C满足2sinA+sinC=2sinB,
建立适当的坐标系,求顶点C的轨迹方程.
解 以AB边所在的直线为x轴,AB的垂直平分线为y轴,
建立平面直角坐标系如图所示,则A(-2,0),B(2,0).
∵2sinA+sinC=2sinB,由正弦定理,
∴2|CB|+|AB|=2|CA|,
从而有|CA|-|CB|=|AB|=2<|AB|.
由双曲线的定义知,点C的轨迹为双曲线的右支(除去与x轴的交点).
∵a=,c=2,∴b2=c2-a2=6,
则顶点C的轨迹方程为-=1(x>).
例5 如图,设 A,B 两点的坐标分别为(-5,0),(5,0),直线 AM,BM 相交于点 M,且它们的斜率之积是,试求点M 的轨迹方程,并由点 M 的轨迹方程判断轨迹的形状,
解 设点M 的坐标为(x,y),
因为点A的坐标为(- 5,0), 所以直线 AM 的斜率kAM=.
同理,直线 BM 的斜率kBM=.
由已知,有×=,
化简,得点M 的轨迹方程为=1(x≠±5).
所以点M 的轨迹是除去(-5,0),(5,0)两点的双曲线.
典例精析
题型二:与双曲线有关的轨迹问题
典例精析
题型二:与双曲线有关的轨迹问题
例6 点P是双曲线-y2=1上一动点,O为坐标原点,M为线段OP的中点,求点M的轨迹方程.
解 设M(x,y),
再设P(x0,y0)为双曲线-y2=1上任意一点,
则∴
∵P为双曲线上任意一点,
∴-4y2=1,即x2-4y2=1.
∴点M的轨迹方程为x2-4y2=1.
例7 由甲导弹驱逐舰、乙导弹驱逐舰、丙综合补给舰组成的护航编队奔赴某海域执行
护航任务,对商船进行护航.某日,甲舰在乙舰正东方向6 km处,丙舰在乙舰北偏西30°
方向,相距4 km处,某时刻甲舰发现商船的求救信号,由于乙、丙两舰比甲舰距商船远,因此4 s后乙、丙两舰才同时发现这一信号,此信号的传播速度为1 km/s,若甲舰赶赴
救援,行进的方向角应是多少?
典例精析
题型三:双曲线方程的应用
解 设A,B,C,P分别表示甲舰、乙舰、丙舰和商船.如图所示,
以直线AB为x 轴,线段AB的垂直平分线为y 轴建立直角坐标系,
则A(3,0),B(-3,0),C(-5,2). ∵|PB|=|PC|,
∴点P在线段BC的垂直平分线上,
又易知kBC=-,线段BC的中点D(-4,),
∴直线PD的方程为y-=(x+4), ①
又|PB|-|PA|=4<6=|AB|,
∴点P在以A,B为焦点的双曲线的右支上,且a=2,c=3,
∴双曲线方程为-=1(x≥2), ②
联立①②,得P点坐标为(8,5),
∴kPA==,
因此甲舰行进的方向角为北偏东30°.
例8 某工程需要开挖一个横截面为半圆的柱形隧道,挖出的土只能沿道路AP,BP
运到P处(如图),|AP|=100 m,|BP|=150 m,∠APB=60°,试说明怎样运土才能最省工.
解 如图,以AB所在的直线为x轴,
AB的垂直平分线为y轴建立平面直角坐标系,
设M是分界线上的点,则|MA|+|AP|=|MB|+|BP|,
即|MA|-|MB|=|BP|-|AP|=150-100=50(m),
这说明分界线是以A,B为焦点的双曲线的右支,且a=25.
典例精析
题型三:双曲线方程的应用
在△APB中,|AB|2=|AP|2+|BP|2-2|AP|·|BP|·cos 60°=17 500,
从而c2=()2=4 375,b2=3 750,
故所求分界线的方程为-=1(x≥25).
即在运土时,将此分界线左侧的土沿道路AP运到P处,
右侧的土沿道路BP运到P处最省工.
跟踪练习
1.已知M(-2,0),N(2,0),|PM|-|PN|=4,则动点P的轨迹是 ( )
A.双曲线 B.双曲线左支
C.一条射线 D.双曲线右支
解 因为|PM|-|PN|=4=|MN|,所以动点P的轨迹是一条射线.
C
跟踪练习
2.已知双曲线=1的左、右焦点分别是F1,F2,若双曲线上一点P使得∠F1PF2=90°,求△F1PF2的面积.
解 在双曲线的方程中,a=3,b=4,则c=5.
设|PF1|=m,|PF2|=n(m>0,n>0).
由双曲线的定义可知,|m-n|=2a=6,
两边平方,得m2+n2-2mn=36.
又∵∠F1PF2=90°,
∴由勾股定理,得m2+n2=|F1F2|2=(2c)2=100.
∴mn=32,∴mn=16.
跟踪练习
3.设双曲线与椭圆=1有共同的焦点,且与椭圆的一个公共点的纵坐标为4,
求双曲线的标准方程.
解 由椭圆方程得焦点坐标为(0,±3),椭圆与双曲线的一个公共点为(,4).
设所求的双曲线方程为=1(a>0,b>0),
则解得
故所求双曲线的标准方程为=1.
4.如图所示,已知定圆F1:x2+y2+10x+24=0,定圆F2:x2+y2-10x+9=0,动圆M与定圆F1,F2都外切,求动圆圆心M的轨迹方程.
解 圆F1:(x+5)2+y2=1,圆心F1(-5,0),半径r1=1.
圆F2:(x-5)2+y2=42,圆心F2(5,0),半径r2=4.
设动圆M的半径为R,则有|MF1|=R+1,|MF2|=R+4,
∴|MF2|-|MF1|=3<10=|F1F2|.
∴点M的轨迹是以F1,F2为焦点的双曲线的左支,
且a=,c=5,于是b2=c2-a2=.
故动圆圆心M的轨迹方程为-=1(x≤).
跟踪练习
跟踪练习
5.已知点M(-3,0),N(3,0),B(1,0),动圆C与直线MN切于点B,过M,N与圆C相切的两直线相交于点P,则P点的轨迹方程为( )
A.x2-=1(x>1) B.x2-=1(x>0)
C.x2-=1(x>0) D.x2-=1(x>1)
解 设过点P的两切线分别与圆切于S,T,
则|PM|-|PN|=(|PS|+|SM|)-(|PT|+|TN|)
=|SM|-|TN|=|BM|-|BN|=4-2=2a,
所以曲线为双曲线的右支且不能与x轴相交,
a=1,c=3,所以b2=8,
故P点的轨迹方程为x2-=1(x>1).
A
跟踪练习
6. 一块面积为12公顷的三角形形状的农场.如图所示△PEF,已知tan∠PEF=,tan∠PFE=-2,试建立适当直角坐标系,求出分别以E,F为左、右焦点且过点P的双曲线方程.
解 以E,F所在直线为x轴,EF的垂直平分线为y轴建立直角坐标系.
设以E,F为焦点且过点P的双曲线方程为=1,
焦点为E(-c,0),F(c,0).
由tan∠PEF=, tan∠EFP=-2,
设∠PFx=α, 则tan α=tan(π-∠EFP)=2,
得直线PE和直线PF的方程分别为y=(x+c)和y=2(x-c).
联立两方程,解得x=c, y=c,
即P点坐标为.
∵在△EFP中,|EF|=2c,EF上的高为点P的纵坐标,
∴S△EFP=c2=12,∴c=3,即P点坐标为(5,4).
由两点间的距离公式|PE|==4,|PF|==2,
∴a=.又b2=c2-a2=4,
故所求双曲线的方程为=1.
课堂小结
本
课
结
束
第三章 圆锥曲线的方程
3.2.1 双曲线及其标准方程
第2课时 双曲线及其标准方程的应用
文字语言 平面内与两个定点F1,F2的距离的__________等于非零
常数(小于|F1F2|)的点的轨迹.
符号语言 ||PF1|-|PF2||=常数(常数<|F1F2|)
焦点 定点__________
焦距 ________的距离
差的绝对值
F1,F2
两焦点间
复习回顾
复习回顾
焦点位置 焦点在x轴上 焦点在y轴上
图形
标准方程 ___________________ ___________________
焦点 ________________ ________________
a,b,c的关系 c2=_______
(-c,0),(c,0)
(0,-c),(0,c)
a2+b2
典例精析
题型一:双曲线定义的应用
例1 如图,若F1,F2是双曲线-=1的两个焦点.
(1)若双曲线上一点P到它的一个焦点的距离等于16,求点P到另一个焦点的距离;
(2)若P是双曲线左支上的点,且|PF1|·|PF2|=32,试求△F1PF2的面积.
解 双曲线的标准方程为-=1,
故a=3,b=4,c=5.
(1)由双曲线的定义得||PF1|-|PF2||=2a=6,
又双曲线上一点P到它的一个焦点的距离等于16,
假设点P到另一个焦点的距离等于x,
则|16-x|=6,解得x=10或x=22.
故点P到另一个焦点的距离为10或22.
典例精析
题型一:双曲线定义的应用
例1 如图,若F1,F2是双曲线-=1的两个焦点.
(1)若双曲线上一点P到它的一个焦点的距离等于16,求点P到另一个焦点的距离;
(2)若P是双曲线左支上的点,且|PF1|·|PF2|=32,试求△F1PF2的面积.
(2)将||PF1|-|PF2|| =2a=6,两边平方得|PF1|2+|PF2|2-2|PF1|·|PF2|=36,
∴|PF1|2+|PF2|2=36+2|PF1|·|PF2|=36+2×32=100.
在△F1PF2中,由余弦定理得
cos ∠F1PF2==0,
∴∠F1PF2=90°,
∴S△F1PF2=|PF1|·|PF2|=×32=16.
典例精析
题型一:双曲线定义的应用
例2 △ABC中,A(-5,0),B(5,0),点C在双曲线-=1上,则=( )
A. B.± C.- D.±
解 在△ABC中,由正弦定理得==.
又∵|BC|-|AC|=±8,∴=±=±.
D
典例精析
题型二:与双曲线有关的轨迹问题
例3 已知两圆C1:(x+4)2+y2=2,C2:(x-4)2+y2=2,动圆M与圆C1外切,与圆C2内切,则动圆圆心M的轨迹方程为 .
解 设动圆圆心M(x,y),半径为r,
因为圆M与圆C1:(x+4)2+y2=2外切,与圆C2:(x-4)2+y2=2内切,
所以|MC1|=r+,|MC2|=r-,|MC1|-|MC2|=2<8.
由双曲线的定义知点M的轨迹
是以C1,C2为焦点的双曲线的右支,且a=,c=4,
故动圆圆心M的轨迹方程为=1(x≥).
=1(x≥)
典例精析
题型二:与双曲线有关的轨迹问题
例4 如图,在△ABC中,已知|AB|=4,且三内角A,B,C满足2sinA+sinC=2sinB,
建立适当的坐标系,求顶点C的轨迹方程.
解 以AB边所在的直线为x轴,AB的垂直平分线为y轴,
建立平面直角坐标系如图所示,则A(-2,0),B(2,0).
∵2sinA+sinC=2sinB,由正弦定理,
∴2|CB|+|AB|=2|CA|,
从而有|CA|-|CB|=|AB|=2<|AB|.
由双曲线的定义知,点C的轨迹为双曲线的右支(除去与x轴的交点).
∵a=,c=2,∴b2=c2-a2=6,
则顶点C的轨迹方程为-=1(x>).
例5 如图,设 A,B 两点的坐标分别为(-5,0),(5,0),直线 AM,BM 相交于点 M,且它们的斜率之积是,试求点M 的轨迹方程,并由点 M 的轨迹方程判断轨迹的形状,
解 设点M 的坐标为(x,y),
因为点A的坐标为(- 5,0), 所以直线 AM 的斜率kAM=.
同理,直线 BM 的斜率kBM=.
由已知,有×=,
化简,得点M 的轨迹方程为=1(x≠±5).
所以点M 的轨迹是除去(-5,0),(5,0)两点的双曲线.
典例精析
题型二:与双曲线有关的轨迹问题
典例精析
题型二:与双曲线有关的轨迹问题
例6 点P是双曲线-y2=1上一动点,O为坐标原点,M为线段OP的中点,求点M的轨迹方程.
解 设M(x,y),
再设P(x0,y0)为双曲线-y2=1上任意一点,
则∴
∵P为双曲线上任意一点,
∴-4y2=1,即x2-4y2=1.
∴点M的轨迹方程为x2-4y2=1.
例7 由甲导弹驱逐舰、乙导弹驱逐舰、丙综合补给舰组成的护航编队奔赴某海域执行
护航任务,对商船进行护航.某日,甲舰在乙舰正东方向6 km处,丙舰在乙舰北偏西30°
方向,相距4 km处,某时刻甲舰发现商船的求救信号,由于乙、丙两舰比甲舰距商船远,因此4 s后乙、丙两舰才同时发现这一信号,此信号的传播速度为1 km/s,若甲舰赶赴
救援,行进的方向角应是多少?
典例精析
题型三:双曲线方程的应用
解 设A,B,C,P分别表示甲舰、乙舰、丙舰和商船.如图所示,
以直线AB为x 轴,线段AB的垂直平分线为y 轴建立直角坐标系,
则A(3,0),B(-3,0),C(-5,2). ∵|PB|=|PC|,
∴点P在线段BC的垂直平分线上,
又易知kBC=-,线段BC的中点D(-4,),
∴直线PD的方程为y-=(x+4), ①
又|PB|-|PA|=4<6=|AB|,
∴点P在以A,B为焦点的双曲线的右支上,且a=2,c=3,
∴双曲线方程为-=1(x≥2), ②
联立①②,得P点坐标为(8,5),
∴kPA==,
因此甲舰行进的方向角为北偏东30°.
例8 某工程需要开挖一个横截面为半圆的柱形隧道,挖出的土只能沿道路AP,BP
运到P处(如图),|AP|=100 m,|BP|=150 m,∠APB=60°,试说明怎样运土才能最省工.
解 如图,以AB所在的直线为x轴,
AB的垂直平分线为y轴建立平面直角坐标系,
设M是分界线上的点,则|MA|+|AP|=|MB|+|BP|,
即|MA|-|MB|=|BP|-|AP|=150-100=50(m),
这说明分界线是以A,B为焦点的双曲线的右支,且a=25.
典例精析
题型三:双曲线方程的应用
在△APB中,|AB|2=|AP|2+|BP|2-2|AP|·|BP|·cos 60°=17 500,
从而c2=()2=4 375,b2=3 750,
故所求分界线的方程为-=1(x≥25).
即在运土时,将此分界线左侧的土沿道路AP运到P处,
右侧的土沿道路BP运到P处最省工.
跟踪练习
1.已知M(-2,0),N(2,0),|PM|-|PN|=4,则动点P的轨迹是 ( )
A.双曲线 B.双曲线左支
C.一条射线 D.双曲线右支
解 因为|PM|-|PN|=4=|MN|,所以动点P的轨迹是一条射线.
C
跟踪练习
2.已知双曲线=1的左、右焦点分别是F1,F2,若双曲线上一点P使得∠F1PF2=90°,求△F1PF2的面积.
解 在双曲线的方程中,a=3,b=4,则c=5.
设|PF1|=m,|PF2|=n(m>0,n>0).
由双曲线的定义可知,|m-n|=2a=6,
两边平方,得m2+n2-2mn=36.
又∵∠F1PF2=90°,
∴由勾股定理,得m2+n2=|F1F2|2=(2c)2=100.
∴mn=32,∴mn=16.
跟踪练习
3.设双曲线与椭圆=1有共同的焦点,且与椭圆的一个公共点的纵坐标为4,
求双曲线的标准方程.
解 由椭圆方程得焦点坐标为(0,±3),椭圆与双曲线的一个公共点为(,4).
设所求的双曲线方程为=1(a>0,b>0),
则解得
故所求双曲线的标准方程为=1.
4.如图所示,已知定圆F1:x2+y2+10x+24=0,定圆F2:x2+y2-10x+9=0,动圆M与定圆F1,F2都外切,求动圆圆心M的轨迹方程.
解 圆F1:(x+5)2+y2=1,圆心F1(-5,0),半径r1=1.
圆F2:(x-5)2+y2=42,圆心F2(5,0),半径r2=4.
设动圆M的半径为R,则有|MF1|=R+1,|MF2|=R+4,
∴|MF2|-|MF1|=3<10=|F1F2|.
∴点M的轨迹是以F1,F2为焦点的双曲线的左支,
且a=,c=5,于是b2=c2-a2=.
故动圆圆心M的轨迹方程为-=1(x≤).
跟踪练习
跟踪练习
5.已知点M(-3,0),N(3,0),B(1,0),动圆C与直线MN切于点B,过M,N与圆C相切的两直线相交于点P,则P点的轨迹方程为( )
A.x2-=1(x>1) B.x2-=1(x>0)
C.x2-=1(x>0) D.x2-=1(x>1)
解 设过点P的两切线分别与圆切于S,T,
则|PM|-|PN|=(|PS|+|SM|)-(|PT|+|TN|)
=|SM|-|TN|=|BM|-|BN|=4-2=2a,
所以曲线为双曲线的右支且不能与x轴相交,
a=1,c=3,所以b2=8,
故P点的轨迹方程为x2-=1(x>1).
A
跟踪练习
6. 一块面积为12公顷的三角形形状的农场.如图所示△PEF,已知tan∠PEF=,tan∠PFE=-2,试建立适当直角坐标系,求出分别以E,F为左、右焦点且过点P的双曲线方程.
解 以E,F所在直线为x轴,EF的垂直平分线为y轴建立直角坐标系.
设以E,F为焦点且过点P的双曲线方程为=1,
焦点为E(-c,0),F(c,0).
由tan∠PEF=, tan∠EFP=-2,
设∠PFx=α, 则tan α=tan(π-∠EFP)=2,
得直线PE和直线PF的方程分别为y=(x+c)和y=2(x-c).
联立两方程,解得x=c, y=c,
即P点坐标为.
∵在△EFP中,|EF|=2c,EF上的高为点P的纵坐标,
∴S△EFP=c2=12,∴c=3,即P点坐标为(5,4).
由两点间的距离公式|PE|==4,|PF|==2,
∴a=.又b2=c2-a2=4,
故所求双曲线的方程为=1.
课堂小结
本
课
结
束
