3.2.2 第1课时 双曲线的简单几何性质 课件(共26张PPT)
文档属性
| 名称 | 3.2.2 第1课时 双曲线的简单几何性质 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 16:50:05 | ||
图片预览



文档简介
(共26张PPT)
3.2.2 双曲线的简单几何性质
第1课时 双曲线的简单几何性质
第三章 圆锥曲线的方程
问题引入
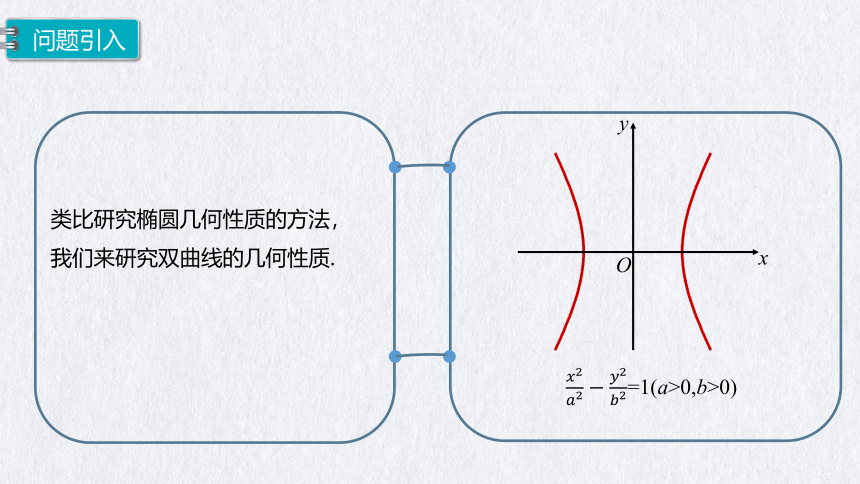
类比研究椭圆几何性质的方法,我们来研究双曲线的几何性质.
O
x
y
=1(a>0,b>0)
新知探索
双曲线的简单几何性质
1.范围
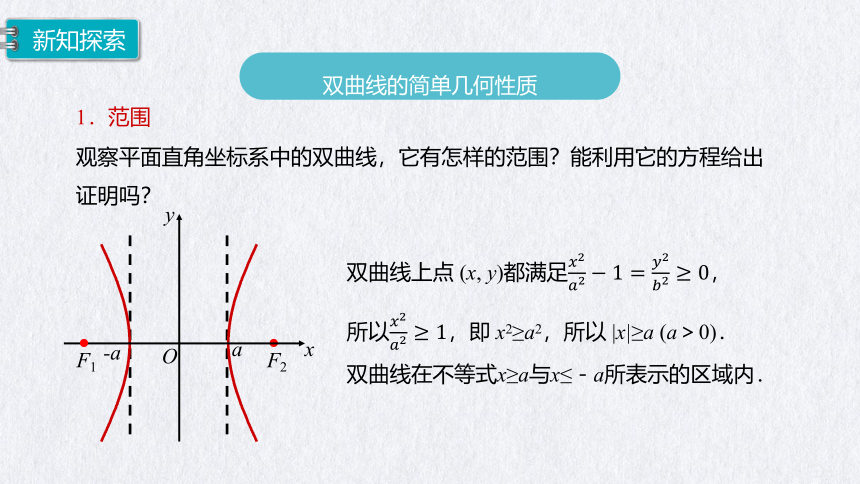
观察平面直角坐标系中的双曲线,它有怎样的范围?能利用它的方程给出证明吗?
a
-a
O
x
F1
F2
y
双曲线上点 (x, y)都满足,
所以,即 x2≥a2,所以 |x|≥a (a>0).
双曲线在不等式x≥a与x≤-a所表示的区域内.
新知探索
双曲线的简单几何性质
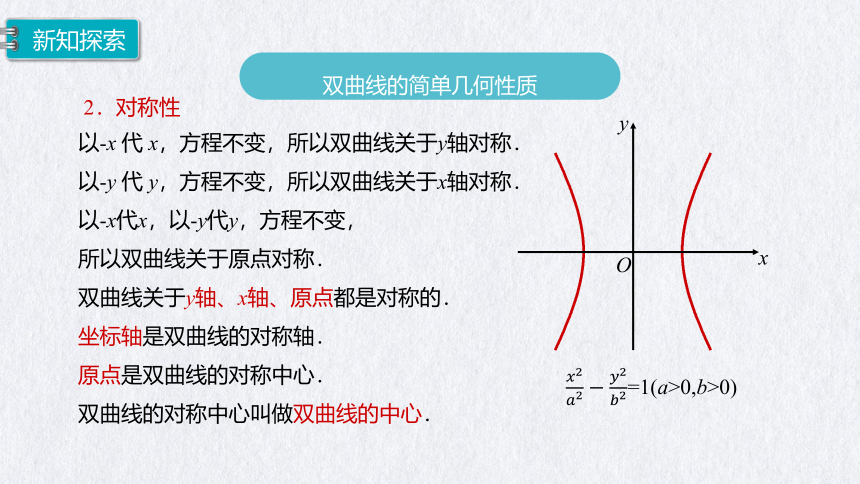
2.对称性
以-x 代 x,方程不变,所以双曲线关于y轴对称.
以-y 代 y,方程不变,所以双曲线关于x轴对称.
以-x代x,以-y代y,方程不变,
所以双曲线关于原点对称.
双曲线关于y轴、x轴、原点都是对称的.
坐标轴是双曲线的对称轴.
原点是双曲线的对称中心.
双曲线的对称中心叫做双曲线的中心.
O
x
y
=1(a>0,b>0)
新知探索
双曲线的简单几何性质
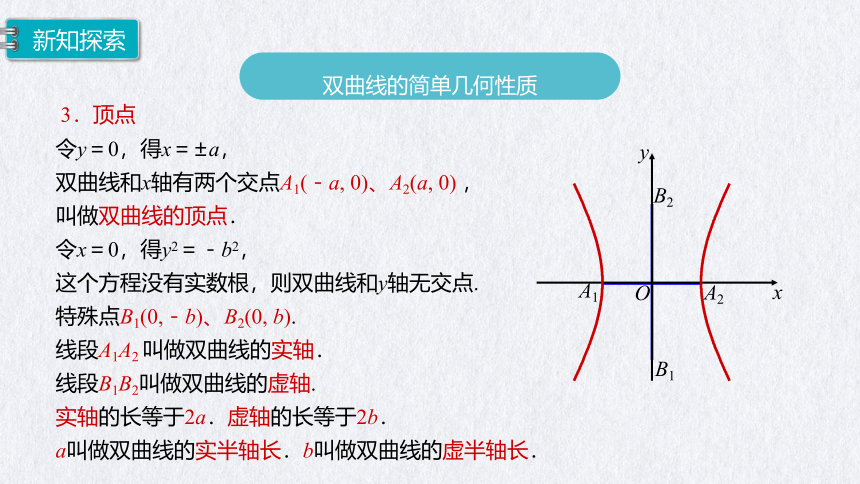
3.顶点
令y=0,得x=±a,
双曲线和x轴有两个交点A1(-a, 0)、A2(a, 0) ,
叫做双曲线的顶点.
令x=0,得y2=-b2,
这个方程没有实数根,则双曲线和y轴无交点.
特殊点B1(0,-b)、B2(0, b).
线段A1A2 叫做双曲线的实轴.
线段B1B2叫做双曲线的虚轴.
实轴的长等于2a.虚轴的长等于2b.
a叫做双曲线的实半轴长.b叫做双曲线的虚半轴长.
y
O
x
A1
A2
B2
B1
新知探索
双曲线的简单几何性质
y
O
x
A1
A2
B2
B1
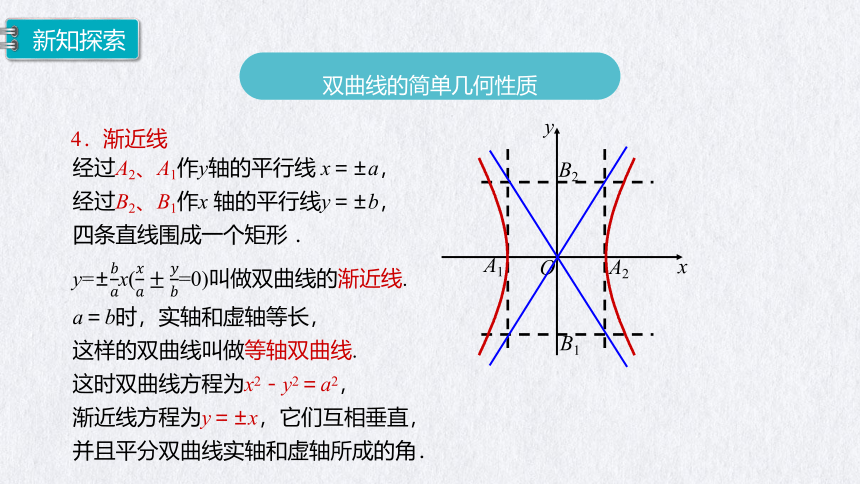
经过A2、A1作y轴的平行线 x=±a,
经过B2、B1作x 轴的平行线y=±b,
四条直线围成一个矩形 .
y=±x(=0)叫做双曲线的渐近线.
a=b时,实轴和虚轴等长,
这样的双曲线叫做等轴双曲线.
这时双曲线方程为x2-y2=a2,
渐近线方程为y=±x,它们互相垂直,并且平分双曲线实轴和虚轴所成的角.
4.渐近线
新知探索
双曲线的简单几何性质
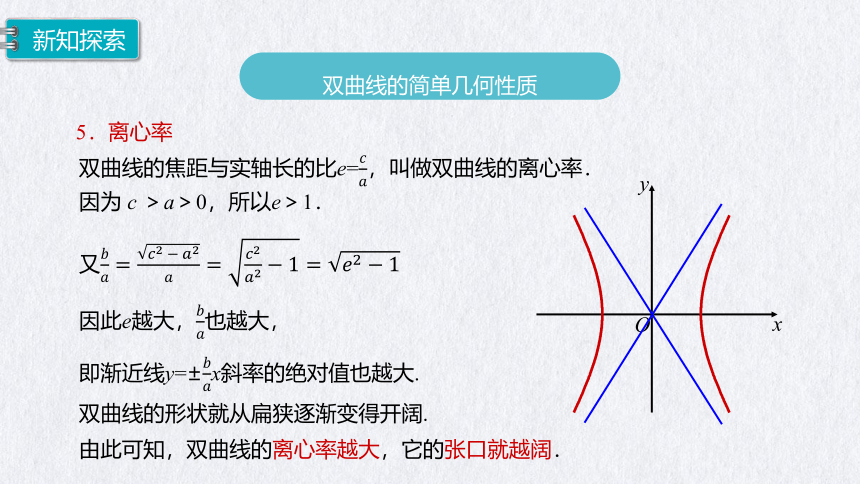
5.离心率
双曲线的焦距与实轴长的比e=,叫做双曲线的离心率.
因为 c >a>0,所以e>1.
又
因此e越大,也越大,
即渐近线y=±x斜率的绝对值也越大.
双曲线的形状就从扁狭逐渐变得开阔.
由此可知,双曲线的离心率越大,它的张口就越阔.
y
O
x
新知探索
双曲线的简单几何性质
标准方程
图形
性质 范围 _____________ ______________
对称性 对称轴:坐标轴;对称中心:原点
顶点坐标 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
渐近线 ________ ________
离心率 e= ,e∈(1,+∞),其中c=
a,b,c间的关系 c2= (c>a>0,c>b>0)
x≥a或x≤-a
y≤-a或y≥a
a2+b2
典例精析
题型一:由双曲线方程研究其几何性质
例1 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率、渐近线方程.
解 将9y2-4x2=-36化为标准方程为-=1,
所以a=3,b=2,c=.
因此顶点坐标为A1(-3,0),A2(3,0),
焦点坐标为F1(-,0),F2(,0),
实轴长2a=6,虚轴长2b=4,
离心率e==,
渐近线方程为y=±x=±x.
典例精析
题型二:由双曲线的几何性质求标准方程
例2 根据以下条件,求双曲线的标准方程.
(1)过点P(3,-),离心率为;
解 (1)若双曲线的焦点在x轴上,
设其方程为=1(a>0,b>0),
∵e=,∴=2,即a2=b2. ①
又双曲线过P(3,-),∴=1, ②
由①②得a2=b2=4,
故双曲线方程为=1.
若双曲线的焦点在y轴上,
设其方程为=1(a>0,b>0),
同理有a2=b2, ③
=1, ④
由③④得a2=b2=-4(舍去).
综上,双曲线的标准方程为=1.
典例精析
题型二:由双曲线的几何性质求标准方程
例2 根据以下条件,求双曲线的标准方程.
(2)与椭圆=1有公共焦点,且离心率e=;
解 (2)由椭圆方程=1,
知半焦距为,
∴焦点是F1(-,0),F2(,0).
因此双曲线的焦点为(-,0),(,0).
设双曲线方程为=1(a>0,b>0),
由已知条件,有
解得
∴所求双曲线的标准方程为-y2=1.
例2 根据以下条件,求双曲线的标准方程.
(3)与双曲线=1有共同渐近线,且过点(-3,2).
典例精析
题型二:由双曲线的几何性质求标准方程
解 (3)设所求双曲线方程为=λ(λ≠0),
将点(-3,2)代入得λ=,
∴双曲线方程为,
即双曲线的标准方程为=1.
典例精析
题型三:求双曲线的离心率
例3 (1)如果双曲线的渐近线方程是y=±x,求离心率.
解 方法一:若双曲线焦点在x轴上,
设双曲线方程为=1(a>0,b>0).
由题意知,又∵c2=a2+b2,
∴e2==1+=1+=,∴e=.
若双曲线的焦点在y轴上,
设双曲线方程为=1(a>0,b>0).
由题意知,
e2==1+=1+=,
∴e=.
综上知e=或e=.
方法二:设具有渐近线y=±x的双曲线方程为
-=λ(λ≠0),即-=1.
若λ>0,焦点在x轴上,
a2=16λ,b2=9λ,c2=a2+b2=25λ,
∴e2==,∴e=.
典例精析
题型三:求双曲线的离心率
例3 (1)如果双曲线的渐近线方程是y=±x,求离心率.
若λ<0,焦点在y轴上,
a2=-9λ,b2=-16λ,
c2=a2+b2=-25λ,
∴e2==,∴e=.
综上知e=或e=.
典例精析
题型三:求双曲线的离心率
解 直线l的方程为=1,
即bx+ay-ab=0.
所以原点到l的距离d=.
由题意,得=c.
所以ab=c2=(a2+b2),
化为a2-4ab+b2=0.
(2)设双曲线=1(b>a>0)的半焦距为c,直线l过点(a,0),(0,b),已知原点
到直线l的距离为c,求双曲线的离心率.
解之,得a=b或a=b(舍去).
所以c==2a.
所以离心率e=2.
典例精析
题型三:求双曲线的离心率
解 在△PF1F2中,
由正弦定理可得,
所以e=,
即|PF1|=|PF2|,
则点P在双曲线的右支上,
且点P不在直线F1F2上.
(3)已知双曲线=1(a>0,b>0)的左、右焦点分别为F1(-c,0),F2(c,0).
若双曲线上存在点P使,则该双曲线的离心率的取值范围是________.
由双曲线的定义知|PF1|-|PF2|=2a,
则|PF2|-|PF2|=2a,即|PF2|=.
又由双曲线的性质知|PF2|>c-a,
则>c-a,即c2-2ac-a2<0,
所以e2-2e-1<0,
解得-+1又e∈(1,+∞),所以e∈(1,+1).
典例精析
题型三:求双曲线的离心率
(4)设双曲线C的中心为点O,若有且只有一对相交于点O,所成角为60°的直线A1B1和A2B2,满足|A1B1|=|A2B2|,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( )
A. (,2] B. [,2) C. (,+∞) D. [,+∞)
解 设双曲线的方程为=1(a>0,b>0),
由|A1B1|=|A2B2|及双曲线的对称性知
A1与A2,B1与B2关于x轴对称,如图.
∵满足条件的直线只有一对,
∴tan30°<≤tan60°,即<≤.∴<≤3.
又b2=c2-a2,
∴<≤3,即∴跟踪练习
1.双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m的值为( )
A.4 B.-4 C.- D.
解 由双曲线方程mx2+y2=1,知m<0,
则双曲线方程可化为y2-=1,
则a2=1,a=1,又虚轴长是实轴长的2倍,
∴b=2,∴-=b2=4,∴m=-.
C
跟踪练习
2.(多选)若双曲线C的一个焦点F(5,0),P是双曲线上一点,且渐近线方程为y=±x,
则下列结论正确的是 ( )
A.C的方程为=1 B.C的离心率为
C.焦点到渐近线的距离为3 D.|PF|的最小值为2
解 双曲线C的一个焦点F(5,0),
且渐近线方程为y=±x,
可得c=5,焦点坐标在x轴上,
所以,因为c=5,所以b=4,a=3,
所以C的方程为=1,A正确;
离心率为e=,B不正确;
焦点到渐近线的距离为d==4,C不正确;
|PF|的最小值为c-a=2,D正确.
AD
√
跟踪练习
又由圆C:x2+y2-10y+21=0,可得圆心为C(0,5),半径r=2,
跟踪练习
4.中心在原点,焦点在x轴上,且一个焦点在直线3x-4y+12=0上的等轴双曲线的方程是 .
解 令y=0,得x=-4,
∴等轴双曲线的一个焦点为(-4,0),
∴c=4,a2=b2=c2=×16=8,
故等轴双曲线的方程为x2-y2=8.
x2-y2=8
跟踪练习
√
跟踪练习
6.求适合下列条件的双曲线的标准方程.
(1)焦点在x轴上,虚轴长为8,离心率为;
(2)过点(2,0),与双曲线=1离心率相等.
解 (1)设方程为=1(a>0,b>0),
由题意知2b=8,e=,
从而b=4,c=a,
代入c2=a2+b2,得a2=9,
故双曲线的标准方程为=1.
(2)由题意知,所求双曲线的焦点在x轴上,
故可设其方程为=λ(λ>0),
将点(2,0)的坐标代入方程得λ=,
故所求双曲线的标准方程为-y2=1.
课堂小结
本
课
结
束
3.2.2 双曲线的简单几何性质
第1课时 双曲线的简单几何性质
第三章 圆锥曲线的方程
问题引入
类比研究椭圆几何性质的方法,我们来研究双曲线的几何性质.
O
x
y
=1(a>0,b>0)
新知探索
双曲线的简单几何性质
1.范围
观察平面直角坐标系中的双曲线,它有怎样的范围?能利用它的方程给出证明吗?
a
-a
O
x
F1
F2
y
双曲线上点 (x, y)都满足,
所以,即 x2≥a2,所以 |x|≥a (a>0).
双曲线在不等式x≥a与x≤-a所表示的区域内.
新知探索
双曲线的简单几何性质
2.对称性
以-x 代 x,方程不变,所以双曲线关于y轴对称.
以-y 代 y,方程不变,所以双曲线关于x轴对称.
以-x代x,以-y代y,方程不变,
所以双曲线关于原点对称.
双曲线关于y轴、x轴、原点都是对称的.
坐标轴是双曲线的对称轴.
原点是双曲线的对称中心.
双曲线的对称中心叫做双曲线的中心.
O
x
y
=1(a>0,b>0)
新知探索
双曲线的简单几何性质
3.顶点
令y=0,得x=±a,
双曲线和x轴有两个交点A1(-a, 0)、A2(a, 0) ,
叫做双曲线的顶点.
令x=0,得y2=-b2,
这个方程没有实数根,则双曲线和y轴无交点.
特殊点B1(0,-b)、B2(0, b).
线段A1A2 叫做双曲线的实轴.
线段B1B2叫做双曲线的虚轴.
实轴的长等于2a.虚轴的长等于2b.
a叫做双曲线的实半轴长.b叫做双曲线的虚半轴长.
y
O
x
A1
A2
B2
B1
新知探索
双曲线的简单几何性质
y
O
x
A1
A2
B2
B1
经过A2、A1作y轴的平行线 x=±a,
经过B2、B1作x 轴的平行线y=±b,
四条直线围成一个矩形 .
y=±x(=0)叫做双曲线的渐近线.
a=b时,实轴和虚轴等长,
这样的双曲线叫做等轴双曲线.
这时双曲线方程为x2-y2=a2,
渐近线方程为y=±x,它们互相垂直,并且平分双曲线实轴和虚轴所成的角.
4.渐近线
新知探索
双曲线的简单几何性质
5.离心率
双曲线的焦距与实轴长的比e=,叫做双曲线的离心率.
因为 c >a>0,所以e>1.
又
因此e越大,也越大,
即渐近线y=±x斜率的绝对值也越大.
双曲线的形状就从扁狭逐渐变得开阔.
由此可知,双曲线的离心率越大,它的张口就越阔.
y
O
x
新知探索
双曲线的简单几何性质
标准方程
图形
性质 范围 _____________ ______________
对称性 对称轴:坐标轴;对称中心:原点
顶点坐标 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
渐近线 ________ ________
离心率 e= ,e∈(1,+∞),其中c=
a,b,c间的关系 c2= (c>a>0,c>b>0)
x≥a或x≤-a
y≤-a或y≥a
a2+b2
典例精析
题型一:由双曲线方程研究其几何性质
例1 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率、渐近线方程.
解 将9y2-4x2=-36化为标准方程为-=1,
所以a=3,b=2,c=.
因此顶点坐标为A1(-3,0),A2(3,0),
焦点坐标为F1(-,0),F2(,0),
实轴长2a=6,虚轴长2b=4,
离心率e==,
渐近线方程为y=±x=±x.
典例精析
题型二:由双曲线的几何性质求标准方程
例2 根据以下条件,求双曲线的标准方程.
(1)过点P(3,-),离心率为;
解 (1)若双曲线的焦点在x轴上,
设其方程为=1(a>0,b>0),
∵e=,∴=2,即a2=b2. ①
又双曲线过P(3,-),∴=1, ②
由①②得a2=b2=4,
故双曲线方程为=1.
若双曲线的焦点在y轴上,
设其方程为=1(a>0,b>0),
同理有a2=b2, ③
=1, ④
由③④得a2=b2=-4(舍去).
综上,双曲线的标准方程为=1.
典例精析
题型二:由双曲线的几何性质求标准方程
例2 根据以下条件,求双曲线的标准方程.
(2)与椭圆=1有公共焦点,且离心率e=;
解 (2)由椭圆方程=1,
知半焦距为,
∴焦点是F1(-,0),F2(,0).
因此双曲线的焦点为(-,0),(,0).
设双曲线方程为=1(a>0,b>0),
由已知条件,有
解得
∴所求双曲线的标准方程为-y2=1.
例2 根据以下条件,求双曲线的标准方程.
(3)与双曲线=1有共同渐近线,且过点(-3,2).
典例精析
题型二:由双曲线的几何性质求标准方程
解 (3)设所求双曲线方程为=λ(λ≠0),
将点(-3,2)代入得λ=,
∴双曲线方程为,
即双曲线的标准方程为=1.
典例精析
题型三:求双曲线的离心率
例3 (1)如果双曲线的渐近线方程是y=±x,求离心率.
解 方法一:若双曲线焦点在x轴上,
设双曲线方程为=1(a>0,b>0).
由题意知,又∵c2=a2+b2,
∴e2==1+=1+=,∴e=.
若双曲线的焦点在y轴上,
设双曲线方程为=1(a>0,b>0).
由题意知,
e2==1+=1+=,
∴e=.
综上知e=或e=.
方法二:设具有渐近线y=±x的双曲线方程为
-=λ(λ≠0),即-=1.
若λ>0,焦点在x轴上,
a2=16λ,b2=9λ,c2=a2+b2=25λ,
∴e2==,∴e=.
典例精析
题型三:求双曲线的离心率
例3 (1)如果双曲线的渐近线方程是y=±x,求离心率.
若λ<0,焦点在y轴上,
a2=-9λ,b2=-16λ,
c2=a2+b2=-25λ,
∴e2==,∴e=.
综上知e=或e=.
典例精析
题型三:求双曲线的离心率
解 直线l的方程为=1,
即bx+ay-ab=0.
所以原点到l的距离d=.
由题意,得=c.
所以ab=c2=(a2+b2),
化为a2-4ab+b2=0.
(2)设双曲线=1(b>a>0)的半焦距为c,直线l过点(a,0),(0,b),已知原点
到直线l的距离为c,求双曲线的离心率.
解之,得a=b或a=b(舍去).
所以c==2a.
所以离心率e=2.
典例精析
题型三:求双曲线的离心率
解 在△PF1F2中,
由正弦定理可得,
所以e=,
即|PF1|=|PF2|,
则点P在双曲线的右支上,
且点P不在直线F1F2上.
(3)已知双曲线=1(a>0,b>0)的左、右焦点分别为F1(-c,0),F2(c,0).
若双曲线上存在点P使,则该双曲线的离心率的取值范围是________.
由双曲线的定义知|PF1|-|PF2|=2a,
则|PF2|-|PF2|=2a,即|PF2|=.
又由双曲线的性质知|PF2|>c-a,
则>c-a,即c2-2ac-a2<0,
所以e2-2e-1<0,
解得-+1
典例精析
题型三:求双曲线的离心率
(4)设双曲线C的中心为点O,若有且只有一对相交于点O,所成角为60°的直线A1B1和A2B2,满足|A1B1|=|A2B2|,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( )
A. (,2] B. [,2) C. (,+∞) D. [,+∞)
解 设双曲线的方程为=1(a>0,b>0),
由|A1B1|=|A2B2|及双曲线的对称性知
A1与A2,B1与B2关于x轴对称,如图.
∵满足条件的直线只有一对,
∴tan30°<≤tan60°,即<≤.∴<≤3.
又b2=c2-a2,
∴<≤3,即
1.双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m的值为( )
A.4 B.-4 C.- D.
解 由双曲线方程mx2+y2=1,知m<0,
则双曲线方程可化为y2-=1,
则a2=1,a=1,又虚轴长是实轴长的2倍,
∴b=2,∴-=b2=4,∴m=-.
C
跟踪练习
2.(多选)若双曲线C的一个焦点F(5,0),P是双曲线上一点,且渐近线方程为y=±x,
则下列结论正确的是 ( )
A.C的方程为=1 B.C的离心率为
C.焦点到渐近线的距离为3 D.|PF|的最小值为2
解 双曲线C的一个焦点F(5,0),
且渐近线方程为y=±x,
可得c=5,焦点坐标在x轴上,
所以,因为c=5,所以b=4,a=3,
所以C的方程为=1,A正确;
离心率为e=,B不正确;
焦点到渐近线的距离为d==4,C不正确;
|PF|的最小值为c-a=2,D正确.
AD
√
跟踪练习
又由圆C:x2+y2-10y+21=0,可得圆心为C(0,5),半径r=2,
跟踪练习
4.中心在原点,焦点在x轴上,且一个焦点在直线3x-4y+12=0上的等轴双曲线的方程是 .
解 令y=0,得x=-4,
∴等轴双曲线的一个焦点为(-4,0),
∴c=4,a2=b2=c2=×16=8,
故等轴双曲线的方程为x2-y2=8.
x2-y2=8
跟踪练习
√
跟踪练习
6.求适合下列条件的双曲线的标准方程.
(1)焦点在x轴上,虚轴长为8,离心率为;
(2)过点(2,0),与双曲线=1离心率相等.
解 (1)设方程为=1(a>0,b>0),
由题意知2b=8,e=,
从而b=4,c=a,
代入c2=a2+b2,得a2=9,
故双曲线的标准方程为=1.
(2)由题意知,所求双曲线的焦点在x轴上,
故可设其方程为=λ(λ>0),
将点(2,0)的坐标代入方程得λ=,
故所求双曲线的标准方程为-y2=1.
课堂小结
本
课
结
束
