3.2.1 第1课时 双曲线及其标准方程 课件(共23张PPT)
文档属性
| 名称 | 3.2.1 第1课时 双曲线及其标准方程 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
3.2.1 双曲线及其标准方程
第1课时 双曲线及其标准方程
第三章 圆锥曲线的方程
问题引入
前面我们已经学习了椭圆,
我们知道平面内与两定点F1、F2的距离的和等于常数2a ( 2a>|F1F2|>0)的点的轨迹为椭圆.
问题引入
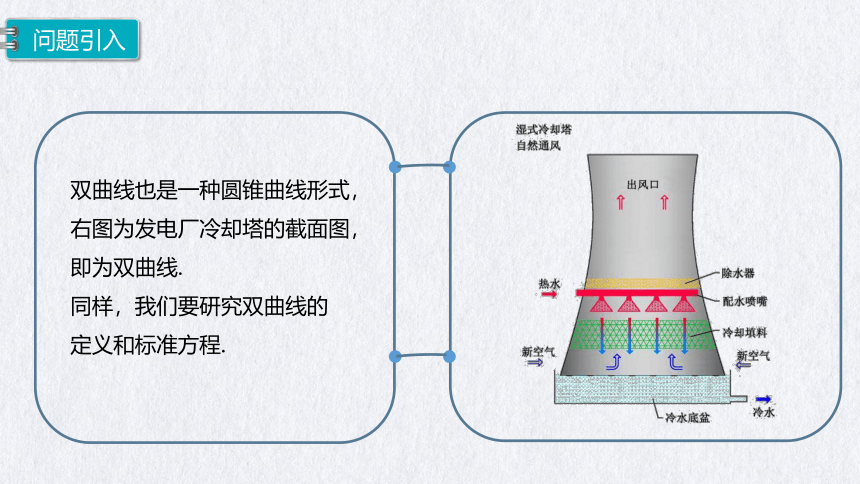
双曲线也是一种圆锥曲线形式,右图为发电厂冷却塔的截面图,即为双曲线.
同样,我们要研究双曲线的
定义和标准方程.
新知探索
双曲线的定义
在直线l上取两个定点A,B,
P是直线l上的动点.
在平面内,取定点F1,F2,
以点F1为圆心、线段PA为半径作圆,
再以F2 为圆心、线段PB为半径作圆.
当点P在线段AB上运动时,
如果|F1F2|其交点M的轨迹是椭圆;
如果|F1F2|>AB,两圆不相交,
不存在交点轨迹.
新知探索
双曲线的定义
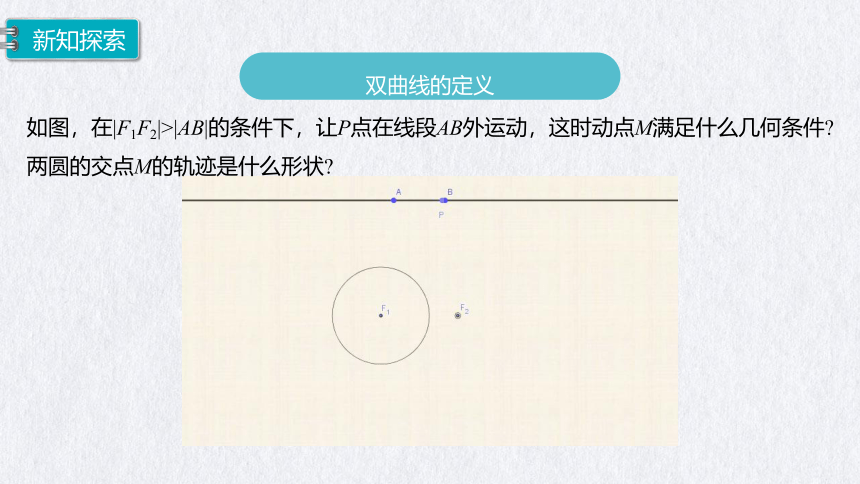
如图,在|F1F2|>|AB|的条件下,让P点在线段AB外运动,这时动点M满足什么几何条件
两圆的交点M的轨迹是什么形状
新知探索
双曲线的定义
总之,点M与两个定点F1,F2距离的差的绝对值|AB|是个常数(|AB|<| F1F2 |),即||MF1|-|MF2||=|AB|.
此时,点M的轨迹是不同于椭圆的曲线,它分为两支,称为双曲线.
新知探索
双曲线的定义
文字语言 平面内与两个定点F1,F2的距离的__________等于非零
常数(小于|F1F2|)的点的轨迹.
符号语言 ||PF1|-|PF2||=常数(常数<|F1F2|)
焦点 定点__________
焦距 ________的距离
差的绝对值
F1,F2
两焦点间
新知探索
双曲线的定义
注意:1.若将定义中差的绝对值中的绝对值符号去掉,则点M的轨迹为
双曲线的一支,具体是哪一支,取决于|MF1|与|MF2|的大小.
(1)若|MF1|>|MF2|,则|MF1|-|MF2|>0,点M的轨迹是靠近定点F2的那一支;
(2)若|MF1|<|MF2|,则|MF2|-|MF1|>0,点M的轨迹是靠近定点F1的那一支.
2.双曲线定义中的常数必须要大于0且小于|F1F2|.
(1)若定义中的常数等于|F1F2|,此时动点轨迹是分别以F1和F2为端点的两条方向相反的射线(包括端点).
(2)若定义中的常数大于|F1F2|,此时动点轨迹不存在.
(3)若定义中的常数为0,此时动点轨迹为线段F1F2的垂直平分线.
新知探索
双曲线的标准方程
O
x
y
即| -|=2a
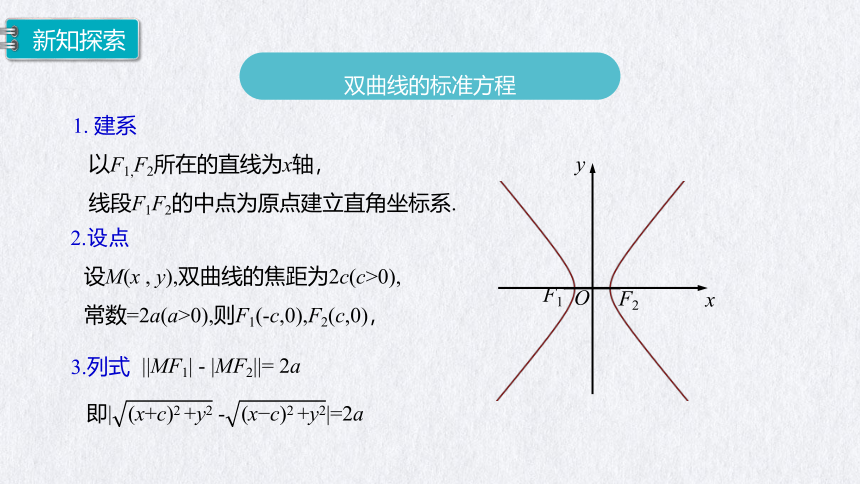
以F1,F2所在的直线为x轴,
线段F1F2的中点为原点建立直角坐标系.
1. 建系
2.设点
3.列式
||MF1| - |MF2||= 2a
设M(x , y),双曲线的焦距为2c(c>0),
常数=2a(a>0),则F1(-c,0),F2(c,0),
F2
F1
新知探索
双曲线的标准方程
4.化简.
| -|=2a
-=±2a
移项两边平方后整理得:cx-a2=±a
两边再平方后整理得:(c2-a2)x2-a2y2=a2(c2-a2)
两边同除以a2(c2-a2)得:=1
设b2=c2-a2(b>0)
代入上式得:=1(a>0,b>0)
新知探索
双曲线的标准方程
焦点在y轴上的双曲线的标准方程是什么?
O
x
y
F2
F1
=1(a>0,b>0)
新知探索
双曲线的标准方程
焦点位置 焦点在x轴上 焦点在y轴上
图形
标准方程 ___________________ ___________________
焦点 ________________ ________________
a,b,c的关系 c2=_______
(-c,0),(c,0)
(0,-c),(0,c)
a2+b2
典例精析
题型一:双曲线的标准方程
例1 (1)已知方程-=1对应的图形是双曲线,那么k的取值范围是 ( )
A.k>5 B.k>5或-2C.k>2或k<-2 D.-2解 ∵方程对应的图形是双曲线,
∴(k-5)(|k|-2)>0.
即 或
解得k>5或-2B
(2)讨论表示何种圆锥曲线,它们有何共同特征.
解 (1)当k < 9时,25-k > 0,9-k >0,所给方程表示椭圆,
由于25-k > 9-k,c2=a2-b2=16,所以这些椭圆的焦点都在 x 轴上,
且焦点坐标都为(-4,0)和(4,0).
(2)当9 < k < 25时,25-k > 0,9-k < 0,所给方程表示双曲线,
其标准方程为.
此时,a2=25-k,b2=k-9,c2=a2+b2=16,
这些双曲线也有共同的焦点(-4,0),(4,0).
(3)当 k > 25 时,所给方程没有轨迹.
典例精析
题型一:双曲线的标准方程
典例精析
题型二:求双曲线的标准方程
例2 求适合下列条件的双曲线的标准方程.
(1)a=3,c=4;
(2)焦点为(0,-6),(0,6),经过点A(-5,6).
解 (1)由题设知,a=3,c=4,
由c2=a2+b2,
得b2=c2-a2=42-32=7.
故双曲线的标准方程为=1或=1.
(2)由已知得c=6,且焦点在y轴上.
因为点A(-5,6)在双曲线上,所以
2a=||
=|13-5|=8,
则a=4,b2=c2-a2=62-42=20.
所以所求双曲线的标准方程是=1.
例3 求适合下列条件的双曲线的标准方程.
(1)焦点在x轴上,a=2,经过点A(-5,2);
(2)经过两点A(-7,-6),B(2,3).
典例精析
题型二:求双曲线的标准方程
解 (1)设双曲线方程为=1(a>0,b>0),
则a=2=1,解得b2=16,
则双曲线的标准方程为=1.
(2)设双曲线方程为mx2-ny2=1,
则有解得
则双曲线的标准方程为=1.
跟踪练习
1.已知两定点F1(-5,0),F2(5,0),动点P满足|PF1|-|PF2|=2a,则当a=3和5时,P点的轨迹为( )
A.双曲线和一条直线
B.双曲线和一条射线
C.双曲线的一支和一条直线
D.双曲线的一支和一条射线
解 当a=3时,根据双曲线的定义及|PF1|>|PF2|可推断出其轨迹是双曲线的一支.
当a=5时,方程y2=0,可知其轨迹与x轴重合,舍去在x轴负半轴上的一段,
又因为|PF1|-|PF2|=2a,说明|PF1|>|PF2|,所以应该是起点为(5,0),与x轴重合
向x轴正方向延伸的射线.
D
跟踪练习
2.已知双曲线=1 (a>0,b>0),F1,F2为其两个焦点,若过焦点F1的直线与双曲线的同一支相交,且所得弦长|AB|=m,则△ABF2的周长为( )
A.4a B.4a-m C.4a+2m D.4a-2m
解 不妨设|AF2|>|AF1|,由双曲线的定义,知|AF2|-|AF1|=2a,|BF2|-|BF1|=2a,
所以|AF2|+|BF2|=(|AF1|+|BF1|)+4a=m+4a,于是△ABF2的周长l=|AF2|+|BF2|+|AB|=4a+2m.故选C.
C
跟踪练习
3.已知方程=1表示双曲线,则m的取值范围是( )
A.(-1,+∞) B.(2,+∞)
C.(-∞,-1)∪(2,+∞) D.(-1,2)
解 ∵方程=1,∴(m-2)(m+1)<0,
解得-1D
跟踪练习
4.求适合下列条件的双曲线的标准方程.
(1)两个焦点的坐标分别是(-5,0),(5,0),双曲线上的点与两焦点的距离之差的绝对值等于8;
(2)以椭圆=1长轴的端点为焦点,且经过点(3,);
(3)a=b,经过点(3,-1).
解 (1)由双曲线的定义知,2a=8,所以a=4,
又知焦点在x轴上,且c=5,
所以b2=c2-a2=25-16=9,
所以双曲线的标准方程为=1.
(2)由题意得,双曲线的焦点在x轴上,且c=2.
设双曲线的标准方程为=1(a>0,b>0),
则有a2+b2=c2=8,=1,
解得a2=3,b2=5.
故所求双曲线的标准方程为=1.
跟踪练习
(3)当焦点在x轴上时,可设双曲线方程为x2-y2=a2,
将点(3,-1)代入,得32-(-1)2=a2,
所以a2=b2=8.因此,所求的双曲线的标准方程为=1.
当焦点在y轴上时,可设双曲线方程为y2-x2=a2,将点(3,-1)代入,
得(-1)2-32=a2,a2=-8,不可能,所以焦点不可能在y轴上.
综上,所求双曲线的标准方程为=1.
课堂小结
本
课
结
束
3.2.1 双曲线及其标准方程
第1课时 双曲线及其标准方程
第三章 圆锥曲线的方程
问题引入
前面我们已经学习了椭圆,
我们知道平面内与两定点F1、F2的距离的和等于常数2a ( 2a>|F1F2|>0)的点的轨迹为椭圆.
问题引入
双曲线也是一种圆锥曲线形式,右图为发电厂冷却塔的截面图,即为双曲线.
同样,我们要研究双曲线的
定义和标准方程.
新知探索
双曲线的定义
在直线l上取两个定点A,B,
P是直线l上的动点.
在平面内,取定点F1,F2,
以点F1为圆心、线段PA为半径作圆,
再以F2 为圆心、线段PB为半径作圆.
当点P在线段AB上运动时,
如果|F1F2|
如果|F1F2|>AB,两圆不相交,
不存在交点轨迹.
新知探索
双曲线的定义
如图,在|F1F2|>|AB|的条件下,让P点在线段AB外运动,这时动点M满足什么几何条件
两圆的交点M的轨迹是什么形状
新知探索
双曲线的定义
总之,点M与两个定点F1,F2距离的差的绝对值|AB|是个常数(|AB|<| F1F2 |),即||MF1|-|MF2||=|AB|.
此时,点M的轨迹是不同于椭圆的曲线,它分为两支,称为双曲线.
新知探索
双曲线的定义
文字语言 平面内与两个定点F1,F2的距离的__________等于非零
常数(小于|F1F2|)的点的轨迹.
符号语言 ||PF1|-|PF2||=常数(常数<|F1F2|)
焦点 定点__________
焦距 ________的距离
差的绝对值
F1,F2
两焦点间
新知探索
双曲线的定义
注意:1.若将定义中差的绝对值中的绝对值符号去掉,则点M的轨迹为
双曲线的一支,具体是哪一支,取决于|MF1|与|MF2|的大小.
(1)若|MF1|>|MF2|,则|MF1|-|MF2|>0,点M的轨迹是靠近定点F2的那一支;
(2)若|MF1|<|MF2|,则|MF2|-|MF1|>0,点M的轨迹是靠近定点F1的那一支.
2.双曲线定义中的常数必须要大于0且小于|F1F2|.
(1)若定义中的常数等于|F1F2|,此时动点轨迹是分别以F1和F2为端点的两条方向相反的射线(包括端点).
(2)若定义中的常数大于|F1F2|,此时动点轨迹不存在.
(3)若定义中的常数为0,此时动点轨迹为线段F1F2的垂直平分线.
新知探索
双曲线的标准方程
O
x
y
即| -|=2a
以F1,F2所在的直线为x轴,
线段F1F2的中点为原点建立直角坐标系.
1. 建系
2.设点
3.列式
||MF1| - |MF2||= 2a
设M(x , y),双曲线的焦距为2c(c>0),
常数=2a(a>0),则F1(-c,0),F2(c,0),
F2
F1
新知探索
双曲线的标准方程
4.化简.
| -|=2a
-=±2a
移项两边平方后整理得:cx-a2=±a
两边再平方后整理得:(c2-a2)x2-a2y2=a2(c2-a2)
两边同除以a2(c2-a2)得:=1
设b2=c2-a2(b>0)
代入上式得:=1(a>0,b>0)
新知探索
双曲线的标准方程
焦点在y轴上的双曲线的标准方程是什么?
O
x
y
F2
F1
=1(a>0,b>0)
新知探索
双曲线的标准方程
焦点位置 焦点在x轴上 焦点在y轴上
图形
标准方程 ___________________ ___________________
焦点 ________________ ________________
a,b,c的关系 c2=_______
(-c,0),(c,0)
(0,-c),(0,c)
a2+b2
典例精析
题型一:双曲线的标准方程
例1 (1)已知方程-=1对应的图形是双曲线,那么k的取值范围是 ( )
A.k>5 B.k>5或-2
∴(k-5)(|k|-2)>0.
即 或
解得k>5或-2
(2)讨论表示何种圆锥曲线,它们有何共同特征.
解 (1)当k < 9时,25-k > 0,9-k >0,所给方程表示椭圆,
由于25-k > 9-k,c2=a2-b2=16,所以这些椭圆的焦点都在 x 轴上,
且焦点坐标都为(-4,0)和(4,0).
(2)当9 < k < 25时,25-k > 0,9-k < 0,所给方程表示双曲线,
其标准方程为.
此时,a2=25-k,b2=k-9,c2=a2+b2=16,
这些双曲线也有共同的焦点(-4,0),(4,0).
(3)当 k > 25 时,所给方程没有轨迹.
典例精析
题型一:双曲线的标准方程
典例精析
题型二:求双曲线的标准方程
例2 求适合下列条件的双曲线的标准方程.
(1)a=3,c=4;
(2)焦点为(0,-6),(0,6),经过点A(-5,6).
解 (1)由题设知,a=3,c=4,
由c2=a2+b2,
得b2=c2-a2=42-32=7.
故双曲线的标准方程为=1或=1.
(2)由已知得c=6,且焦点在y轴上.
因为点A(-5,6)在双曲线上,所以
2a=||
=|13-5|=8,
则a=4,b2=c2-a2=62-42=20.
所以所求双曲线的标准方程是=1.
例3 求适合下列条件的双曲线的标准方程.
(1)焦点在x轴上,a=2,经过点A(-5,2);
(2)经过两点A(-7,-6),B(2,3).
典例精析
题型二:求双曲线的标准方程
解 (1)设双曲线方程为=1(a>0,b>0),
则a=2=1,解得b2=16,
则双曲线的标准方程为=1.
(2)设双曲线方程为mx2-ny2=1,
则有解得
则双曲线的标准方程为=1.
跟踪练习
1.已知两定点F1(-5,0),F2(5,0),动点P满足|PF1|-|PF2|=2a,则当a=3和5时,P点的轨迹为( )
A.双曲线和一条直线
B.双曲线和一条射线
C.双曲线的一支和一条直线
D.双曲线的一支和一条射线
解 当a=3时,根据双曲线的定义及|PF1|>|PF2|可推断出其轨迹是双曲线的一支.
当a=5时,方程y2=0,可知其轨迹与x轴重合,舍去在x轴负半轴上的一段,
又因为|PF1|-|PF2|=2a,说明|PF1|>|PF2|,所以应该是起点为(5,0),与x轴重合
向x轴正方向延伸的射线.
D
跟踪练习
2.已知双曲线=1 (a>0,b>0),F1,F2为其两个焦点,若过焦点F1的直线与双曲线的同一支相交,且所得弦长|AB|=m,则△ABF2的周长为( )
A.4a B.4a-m C.4a+2m D.4a-2m
解 不妨设|AF2|>|AF1|,由双曲线的定义,知|AF2|-|AF1|=2a,|BF2|-|BF1|=2a,
所以|AF2|+|BF2|=(|AF1|+|BF1|)+4a=m+4a,于是△ABF2的周长l=|AF2|+|BF2|+|AB|=4a+2m.故选C.
C
跟踪练习
3.已知方程=1表示双曲线,则m的取值范围是( )
A.(-1,+∞) B.(2,+∞)
C.(-∞,-1)∪(2,+∞) D.(-1,2)
解 ∵方程=1,∴(m-2)(m+1)<0,
解得-1
跟踪练习
4.求适合下列条件的双曲线的标准方程.
(1)两个焦点的坐标分别是(-5,0),(5,0),双曲线上的点与两焦点的距离之差的绝对值等于8;
(2)以椭圆=1长轴的端点为焦点,且经过点(3,);
(3)a=b,经过点(3,-1).
解 (1)由双曲线的定义知,2a=8,所以a=4,
又知焦点在x轴上,且c=5,
所以b2=c2-a2=25-16=9,
所以双曲线的标准方程为=1.
(2)由题意得,双曲线的焦点在x轴上,且c=2.
设双曲线的标准方程为=1(a>0,b>0),
则有a2+b2=c2=8,=1,
解得a2=3,b2=5.
故所求双曲线的标准方程为=1.
跟踪练习
(3)当焦点在x轴上时,可设双曲线方程为x2-y2=a2,
将点(3,-1)代入,得32-(-1)2=a2,
所以a2=b2=8.因此,所求的双曲线的标准方程为=1.
当焦点在y轴上时,可设双曲线方程为y2-x2=a2,将点(3,-1)代入,
得(-1)2-32=a2,a2=-8,不可能,所以焦点不可能在y轴上.
综上,所求双曲线的标准方程为=1.
课堂小结
本
课
结
束
