1.4.2 第2课时 夹角问题 课件(共20张PPT)
文档属性
| 名称 | 1.4.2 第2课时 夹角问题 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 17:05:26 | ||
图片预览






文档简介
(共20张PPT)
1.4.2 用空间向量研究距离、夹角问题
1.4.2 第2课时 夹角问题
第一章 空间向量与立体几何
学习目标:
1.会用向量法求线线、线面、面面夹角.
2.能正确区分向量夹角与所求线线角、线面角、面面角的关系.
学习重点:会用向量法求线线、线面、面面夹角.
学习难点:会用向量法求线线、线面、面面夹角.
空间向量的引入为代数方法处理立体几何问题提供了一种重要的工具和方法,解题时,可用定量的计算代替定性的分析,从而避免了一些繁琐的推理论证.求空间角是立体几何的一类重要的问题,也是高考的热点之一.
引入课题
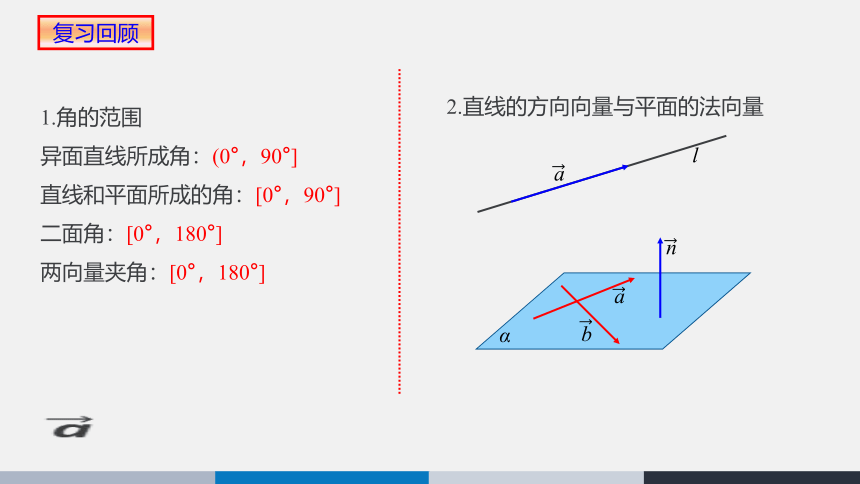
1.角的范围
异面直线所成角:(0°,90°]
直线和平面所成的角:[0°,90°]
二面角:[0°,180°]
两向量夹角:[0°,180°]
2.直线的方向向量与平面的法向量
l
α
复习回顾
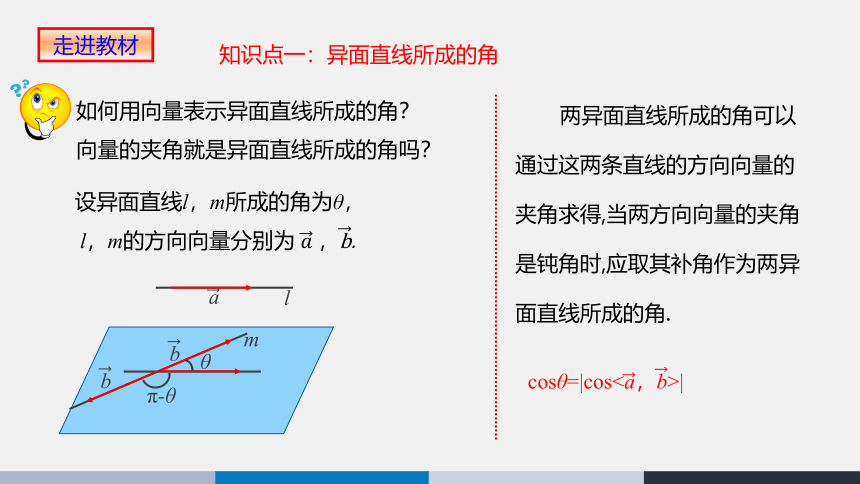
知识点一:异面直线所成的角
如何用向量表示异面直线所成的角?
向量的夹角就是异面直线所成的角吗?
两异面直线所成的角可以
通过这两条直线的方向向量的
夹角求得,当两方向向量的夹角
是钝角时,应取其补角作为两异
面直线所成的角.
cosθ=|cos<,>|
走进教材
θ
π-θ
m
l
设异面直线l,m所成的角为θ,
l,m的方向向量分别为 ,.
解
例1 正方体ABCD-A1B1C1D1中,E、F分别是A1D1、A1C1的中点,
求异面直线AE与CF所成角的余弦值.
D1
D
A
B
C
A1
B1
C1
z
y
x
F
E
不妨设正方体棱长为2,如图建立坐标系,
则A(2,0,0)、C(0,2,0)、
E(1,0,2)、F(1,1,2),
典例分析
则=(-1,0,2),=(1,-1,2),
∴| |=,| |=.
· =-1+0+4=3.
又 · =||||cos< >
=cos< >,
∴cos< >=,
∴所求值为.
正值
典例分析
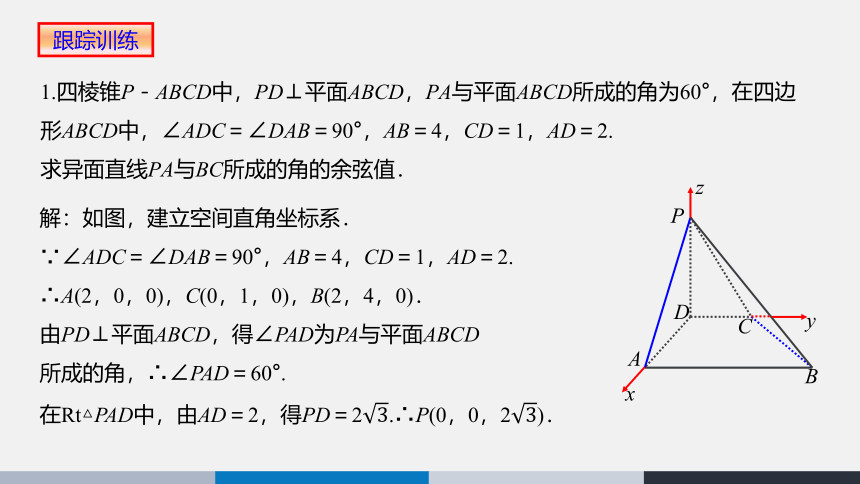
解:如图,建立空间直角坐标系.
∵∠ADC=∠DAB=90°,AB=4,CD=1,AD=2.
∴A(2,0,0),C(0,1,0),B(2,4,0).
由PD⊥平面ABCD,得∠PAD为PA与平面ABCD
所成的角,∴∠PAD=60°.
1.四棱锥P-ABCD中,PD⊥平面ABCD,PA与平面ABCD所成的角为60°,在四边形ABCD中,∠ADC=∠DAB=90°,AB=4,CD=1,AD=2.
求异面直线PA与BC所成的角的余弦值.
D
P
A
B
C
z
y
x
跟踪训练
在Rt△PAD中,由AD=2,得PD=2.∴P(0,0,2).
得=(2,0,-2),=(-2,-3,0),
∴| |=4,| |=,
·=-4,
∴cos< ,>==-,
即PA与BC所成角的余弦值为.
负值
跟踪训练
知识点二:直线与平面所成的角
如何用向量表示直线与平面所成的角?
向量的夹角就是直线与平面所成的角吗?
设直线l与平面α所成的角为θ,
l的方向向量, α的法向量为.
θ
α
l
θ=90°-<, >
或θ=<>-90°
sinθ=±cos<, >
sinθ=|cos<>| .
走进教材
例2 正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为a,
求AC1与侧面ABB1A1所成的角θ.
C1
C
A
B
A1
B1
z
y
x
解 建立如图所示的空间直角坐标系,
则A(0,0,0),C (-a,,0) ,
C1(-a,, a),
∴= (-a,, a).
x
y
A
B
C
a
易求法向量
求坐标非常关键
典例分析
显然可取面ABB1A1的一个法向量为=(1,0,0),
则||=a,· = -a,
∴cos<, >,
即sinθ= ,
又θ∈(0°,90°),
∴ θ=30°.
典例分析
2.已知正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为a,
M为A1B1的中点,求BC1与平面AMC1所成角的正弦值.
C1
C
A
A1
B1
z
y
x
B
O
M
解:取AC的中点O,如图建立坐标系,
则A(,0,0),C1(-,0,a),B(0,a,0),
A1 (,0,a),B1(0,a,a),
跟踪训练
∵ M为A1B1的中点,∴M(a,a),
∴, =(-,0,a),=(-,-a,a),
则·=(-, -,)·(4, -4, 2)
=8,
设面AMC1的法向量为=(x,y,z),
由· =0, · =0,
得, -,
即, -,
令z=2,得x=4,y=-4,
∴ =(4, -4, 2),
跟踪训练
又||=,||=,
∴cos<, >=,
∴所求角的正弦值为.
知识点三:平面与平面所成的角
如何用向量表示平面与平面所成的角?
向量的夹角就是平面与平面所成的角吗?
设平面α与平面β所成的角为θ,
α、β的法向量分别为.
α
β
两法向量所成的角
与二面角的平面角
相等或者互补:
同进同出,二面角
等于法向量夹角的补角;
一进一出,二面角
等于法向量夹角.
走进教材
解 如图所示,取BC中点O,连结AO.
因为△ABC是正三角形,所以AO⊥BC,
因为在正三棱柱ABC — A1B1C1中,
平面ABC⊥平面BCC1B1,
所以AO⊥平面BCC1B1.
以O为原点,如图建立空间直角坐标系,
例3 如图所示,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点,
求二面角A -A1D -B的余弦值.
C1
C
A
B
A1
B1
O
z
y
x
典例分析
则B(1,0,0),D(-1,1,0),
A1(0,2,),A(0,0,),B1(1,2,0).
典例分析
设平面A1AD的法向量为=(x,y,z),
=(-1,1,-),=(0,2,0).
因为⊥,⊥,
得=0,=0,
得-x+y-z=0, y=0,
令z=1,得=(-,0,1)为平面A1AD的一个法向量.
又因为=(1,2,-),=(-2,1,0),
=(-1,2,),所以· =-2+2+0=0,
· =-1+4-3=0,
所以⊥ , ⊥ ,所以AB1⊥平面A1BD,
所以是平面A1BD的一个法向量,
所以cos<, >===-,
所以二面角A A1D B的余弦值为.
典例分析
随堂练习
1.正方体ABCD-A1B1C1D1中,BB1与平面ACD1所成角的正弦值为________.
2.已知两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面夹角为( )
A.45° B.135°
C.45°或135° D.90°
A
3.正方形ABCD所在平面外一点P,PA⊥平面ABCD,若PA=AB,则平面PAB与平面PCD的夹角为( )
A.30° B.45° C.60° D.90°
B
用空间向量解决立体几何问题的“三步曲”.
(1)建立立体图形与空间向量的联系,用空间向量表示问题中
涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置
关系以及它们之间距离和夹角等问题;
(3)把向量的运算结果“翻译”成相应的几何意义.
(化为向量问题)
(进行向量运算)
(回到图形问题)
课堂小结
1.4.2 用空间向量研究距离、夹角问题
1.4.2 第2课时 夹角问题
第一章 空间向量与立体几何
学习目标:
1.会用向量法求线线、线面、面面夹角.
2.能正确区分向量夹角与所求线线角、线面角、面面角的关系.
学习重点:会用向量法求线线、线面、面面夹角.
学习难点:会用向量法求线线、线面、面面夹角.
空间向量的引入为代数方法处理立体几何问题提供了一种重要的工具和方法,解题时,可用定量的计算代替定性的分析,从而避免了一些繁琐的推理论证.求空间角是立体几何的一类重要的问题,也是高考的热点之一.
引入课题
1.角的范围
异面直线所成角:(0°,90°]
直线和平面所成的角:[0°,90°]
二面角:[0°,180°]
两向量夹角:[0°,180°]
2.直线的方向向量与平面的法向量
l
α
复习回顾
知识点一:异面直线所成的角
如何用向量表示异面直线所成的角?
向量的夹角就是异面直线所成的角吗?
两异面直线所成的角可以
通过这两条直线的方向向量的
夹角求得,当两方向向量的夹角
是钝角时,应取其补角作为两异
面直线所成的角.
cosθ=|cos<,>|
走进教材
θ
π-θ
m
l
设异面直线l,m所成的角为θ,
l,m的方向向量分别为 ,.
解
例1 正方体ABCD-A1B1C1D1中,E、F分别是A1D1、A1C1的中点,
求异面直线AE与CF所成角的余弦值.
D1
D
A
B
C
A1
B1
C1
z
y
x
F
E
不妨设正方体棱长为2,如图建立坐标系,
则A(2,0,0)、C(0,2,0)、
E(1,0,2)、F(1,1,2),
典例分析
则=(-1,0,2),=(1,-1,2),
∴| |=,| |=.
· =-1+0+4=3.
又 · =||||cos< >
=cos< >,
∴cos< >=,
∴所求值为.
正值
典例分析
解:如图,建立空间直角坐标系.
∵∠ADC=∠DAB=90°,AB=4,CD=1,AD=2.
∴A(2,0,0),C(0,1,0),B(2,4,0).
由PD⊥平面ABCD,得∠PAD为PA与平面ABCD
所成的角,∴∠PAD=60°.
1.四棱锥P-ABCD中,PD⊥平面ABCD,PA与平面ABCD所成的角为60°,在四边形ABCD中,∠ADC=∠DAB=90°,AB=4,CD=1,AD=2.
求异面直线PA与BC所成的角的余弦值.
D
P
A
B
C
z
y
x
跟踪训练
在Rt△PAD中,由AD=2,得PD=2.∴P(0,0,2).
得=(2,0,-2),=(-2,-3,0),
∴| |=4,| |=,
·=-4,
∴cos< ,>==-,
即PA与BC所成角的余弦值为.
负值
跟踪训练
知识点二:直线与平面所成的角
如何用向量表示直线与平面所成的角?
向量的夹角就是直线与平面所成的角吗?
设直线l与平面α所成的角为θ,
l的方向向量, α的法向量为.
θ
α
l
θ=90°-<, >
或θ=<>-90°
sinθ=±cos<, >
sinθ=|cos<>| .
走进教材
例2 正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为a,
求AC1与侧面ABB1A1所成的角θ.
C1
C
A
B
A1
B1
z
y
x
解 建立如图所示的空间直角坐标系,
则A(0,0,0),C (-a,,0) ,
C1(-a,, a),
∴= (-a,, a).
x
y
A
B
C
a
易求法向量
求坐标非常关键
典例分析
显然可取面ABB1A1的一个法向量为=(1,0,0),
则||=a,· = -a,
∴cos<, >,
即sinθ= ,
又θ∈(0°,90°),
∴ θ=30°.
典例分析
2.已知正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为a,
M为A1B1的中点,求BC1与平面AMC1所成角的正弦值.
C1
C
A
A1
B1
z
y
x
B
O
M
解:取AC的中点O,如图建立坐标系,
则A(,0,0),C1(-,0,a),B(0,a,0),
A1 (,0,a),B1(0,a,a),
跟踪训练
∵ M为A1B1的中点,∴M(a,a),
∴, =(-,0,a),=(-,-a,a),
则·=(-, -,)·(4, -4, 2)
=8,
设面AMC1的法向量为=(x,y,z),
由· =0, · =0,
得, -,
即, -,
令z=2,得x=4,y=-4,
∴ =(4, -4, 2),
跟踪训练
又||=,||=,
∴cos<, >=,
∴所求角的正弦值为.
知识点三:平面与平面所成的角
如何用向量表示平面与平面所成的角?
向量的夹角就是平面与平面所成的角吗?
设平面α与平面β所成的角为θ,
α、β的法向量分别为.
α
β
两法向量所成的角
与二面角的平面角
相等或者互补:
同进同出,二面角
等于法向量夹角的补角;
一进一出,二面角
等于法向量夹角.
走进教材
解 如图所示,取BC中点O,连结AO.
因为△ABC是正三角形,所以AO⊥BC,
因为在正三棱柱ABC — A1B1C1中,
平面ABC⊥平面BCC1B1,
所以AO⊥平面BCC1B1.
以O为原点,如图建立空间直角坐标系,
例3 如图所示,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点,
求二面角A -A1D -B的余弦值.
C1
C
A
B
A1
B1
O
z
y
x
典例分析
则B(1,0,0),D(-1,1,0),
A1(0,2,),A(0,0,),B1(1,2,0).
典例分析
设平面A1AD的法向量为=(x,y,z),
=(-1,1,-),=(0,2,0).
因为⊥,⊥,
得=0,=0,
得-x+y-z=0, y=0,
令z=1,得=(-,0,1)为平面A1AD的一个法向量.
又因为=(1,2,-),=(-2,1,0),
=(-1,2,),所以· =-2+2+0=0,
· =-1+4-3=0,
所以⊥ , ⊥ ,所以AB1⊥平面A1BD,
所以是平面A1BD的一个法向量,
所以cos<, >===-,
所以二面角A A1D B的余弦值为.
典例分析
随堂练习
1.正方体ABCD-A1B1C1D1中,BB1与平面ACD1所成角的正弦值为________.
2.已知两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面夹角为( )
A.45° B.135°
C.45°或135° D.90°
A
3.正方形ABCD所在平面外一点P,PA⊥平面ABCD,若PA=AB,则平面PAB与平面PCD的夹角为( )
A.30° B.45° C.60° D.90°
B
用空间向量解决立体几何问题的“三步曲”.
(1)建立立体图形与空间向量的联系,用空间向量表示问题中
涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置
关系以及它们之间距离和夹角等问题;
(3)把向量的运算结果“翻译”成相应的几何意义.
(化为向量问题)
(进行向量运算)
(回到图形问题)
课堂小结
