2.2.1 直线的点斜式方程 课件(共17张PPT)
文档属性
| 名称 | 2.2.1 直线的点斜式方程 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1011.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 17:06:50 | ||
图片预览





文档简介
(共17张PPT)
第二章 直线与圆的方程
§2.2 直线的方程
2.2.1 直线的点斜式方程
1.掌握直线方程的点斜式和斜截式,并会用它们求直线的方程.(数学运算)
2.了解直线的斜截式方程与一次函数的关系.(数学抽象)
3.会用直线的点斜式方程与斜截式方程解决直线的平行与垂直问题.(数学运算)
学习目标
1.直线的斜率公式
注意:
不是所有的直线都有斜率,
斜率不存在的直线为与 轴垂直的直线.
y
y
-
)
(
)
2
1
2
1
2
1
2
x
x
x
x
k
-
=
)
90
(
tan
)
1
0
k
=
a
a
复习回顾
平行:
l1∥l2 k1=k2.
垂直:
l1⊥l2 k1k2=-1.
条件:不重合、都有斜率
条件:都有斜率
2.两条直线平行与垂直的判定
对于两条不重合的直线l1、l2,其斜率分别为k1、k2,有
复习回顾
问题1
在直角坐标系内确定一条直线,需要哪些几何要素?
1)已知直线上一点 P0(x0,y0) 和直线的倾斜角(或斜率 k).
2)已知直线上两点P1(x1,y1)、P2(x2,y2) .
问题2
能否用给定的条件(点P0和斜率 k或P1、P2的坐标),将直线上所有点的坐标(x,y)满足的关系表示出来 ?
新知探究
根据经过两点的直线斜率公式,得
设点P(x,y)是直线l上不同于P0的任意一点.
O
x
y
.
P0
.
P
可化为
l
1.过点 , 斜率为k的直线l上的每一点的坐标都满足方程.
说明
2.坐标满足方程的每一点都在过点 ,斜率为k 的直线l上.
新知探究
在平面直角坐标系内,如果给定一条直线l经过的一个点 和斜率k,能否将直线上所有的点的坐标(x,y) 满足的关系表示出来呢?
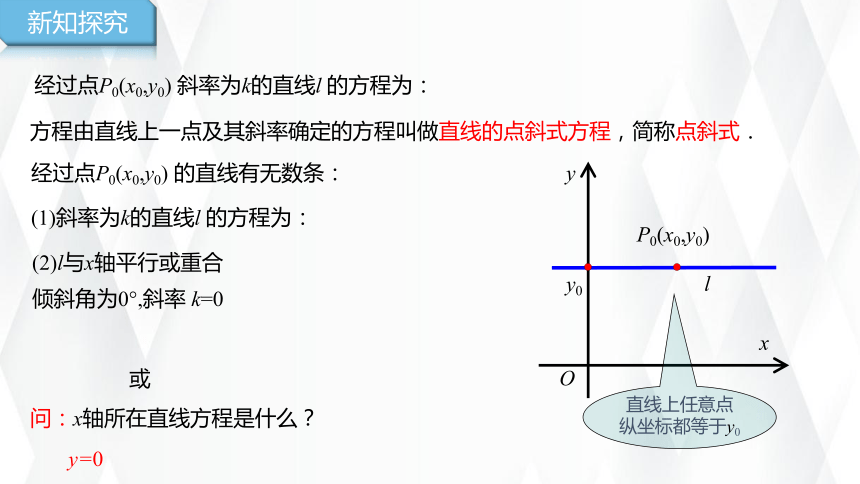
方程由直线上一点及其斜率确定的方程叫做直线的点斜式方程,简称点斜式.
l
x
y
O
P0(x0,y0)
(2)l与x轴平行或重合
倾斜角为0°,斜率 k=0
y0
直线上任意点
纵坐标都等于y0
问:x轴所在直线方程是什么?
y=0
经过点P0(x0,y0) 的直线有无数条:
或
(1)斜率为k的直线l 的方程为:
新知探究
经过点P0(x0,y0) 斜率为k的直线l 的方程为:
问:y轴所在直线方程是什么?
x=0
x
y
l
直线上任意点
横坐标都等于x0
O
P0(x0,y0)
(3)当直线l的倾斜角为 90°时,l与x轴垂直,斜率 k 不存在,不能用点斜式求方程.
或
新知探究
例1 直线l经过点P0(-2,3),且倾斜角α=45°,求直线l的点斜式方程,并画出图像.
代入点斜式方程得:
y-3=x+2 .
解:直线 l 经过点P0(-2,3) ,斜率k=tan45°=1
y
1
2
3
4
x
O
-1
-2
l
典例精讲
例2 已知直线l过A(3,-5)和B(-2,5),求直线l的方程.
解: ∵直线l过点A(3,-5)和B(-2,5),
将A(3,-5),k=-2代入点斜式,得
y-(-5) =-2 ( x-3 ) .
典例精讲
O
x
y
.
(0,b)
已知直线l的斜率是k,与y轴的交点是P(0,b),求直线方程.
代入点斜式方程,得l的直线方程:
y-b=k(x-0).
即y=kx+b .
定义 直线l与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距.
方程是由直线的斜率k与它在y轴上的截距b确定,所以方程叫做直线的斜截式方程,简称斜截式.
l
说明:1.用斜截式方程表示直角坐标平面内的直线斜率必须存在.
2.截距与距离不一样,截距可正、可为零、可负, 而距离不能为负.
3.直线方程的斜截式即是一次函数.
新知探究
例3 求满足下列条件的m的值.
(1)直线l1:y=-x+1与直线l2:y=(m2-2)x+2m平行;
(2)直线l1:y=-2x+3与直线l2:y=(2m-1)x-5垂直.
典例精讲
巩固练习
巩固练习
巩固练习
注意:直线的点斜式,斜截式方程在直线斜率存在时才可以应用.
2.斜截式方程: y = kx +b
1.点斜式方程: y-y0=k(x-x0)
4.直线l1:y=k1x +b1,l2:y=k2x+b2
几何意义:k 是直线的斜率,b是直线在y轴上的截距
3.直线与x轴垂直时,倾斜角=90°
或
课堂小结
本课结束
第二章 直线与圆的方程
§2.2 直线的方程
2.2.1 直线的点斜式方程
1.掌握直线方程的点斜式和斜截式,并会用它们求直线的方程.(数学运算)
2.了解直线的斜截式方程与一次函数的关系.(数学抽象)
3.会用直线的点斜式方程与斜截式方程解决直线的平行与垂直问题.(数学运算)
学习目标
1.直线的斜率公式
注意:
不是所有的直线都有斜率,
斜率不存在的直线为与 轴垂直的直线.
y
y
-
)
(
)
2
1
2
1
2
1
2
x
x
x
x
k
-
=
)
90
(
tan
)
1
0
k
=
a
a
复习回顾
平行:
l1∥l2 k1=k2.
垂直:
l1⊥l2 k1k2=-1.
条件:不重合、都有斜率
条件:都有斜率
2.两条直线平行与垂直的判定
对于两条不重合的直线l1、l2,其斜率分别为k1、k2,有
复习回顾
问题1
在直角坐标系内确定一条直线,需要哪些几何要素?
1)已知直线上一点 P0(x0,y0) 和直线的倾斜角(或斜率 k).
2)已知直线上两点P1(x1,y1)、P2(x2,y2) .
问题2
能否用给定的条件(点P0和斜率 k或P1、P2的坐标),将直线上所有点的坐标(x,y)满足的关系表示出来 ?
新知探究
根据经过两点的直线斜率公式,得
设点P(x,y)是直线l上不同于P0的任意一点.
O
x
y
.
P0
.
P
可化为
l
1.过点 , 斜率为k的直线l上的每一点的坐标都满足方程.
说明
2.坐标满足方程的每一点都在过点 ,斜率为k 的直线l上.
新知探究
在平面直角坐标系内,如果给定一条直线l经过的一个点 和斜率k,能否将直线上所有的点的坐标(x,y) 满足的关系表示出来呢?
方程由直线上一点及其斜率确定的方程叫做直线的点斜式方程,简称点斜式.
l
x
y
O
P0(x0,y0)
(2)l与x轴平行或重合
倾斜角为0°,斜率 k=0
y0
直线上任意点
纵坐标都等于y0
问:x轴所在直线方程是什么?
y=0
经过点P0(x0,y0) 的直线有无数条:
或
(1)斜率为k的直线l 的方程为:
新知探究
经过点P0(x0,y0) 斜率为k的直线l 的方程为:
问:y轴所在直线方程是什么?
x=0
x
y
l
直线上任意点
横坐标都等于x0
O
P0(x0,y0)
(3)当直线l的倾斜角为 90°时,l与x轴垂直,斜率 k 不存在,不能用点斜式求方程.
或
新知探究
例1 直线l经过点P0(-2,3),且倾斜角α=45°,求直线l的点斜式方程,并画出图像.
代入点斜式方程得:
y-3=x+2 .
解:直线 l 经过点P0(-2,3) ,斜率k=tan45°=1
y
1
2
3
4
x
O
-1
-2
l
典例精讲
例2 已知直线l过A(3,-5)和B(-2,5),求直线l的方程.
解: ∵直线l过点A(3,-5)和B(-2,5),
将A(3,-5),k=-2代入点斜式,得
y-(-5) =-2 ( x-3 ) .
典例精讲
O
x
y
.
(0,b)
已知直线l的斜率是k,与y轴的交点是P(0,b),求直线方程.
代入点斜式方程,得l的直线方程:
y-b=k(x-0).
即y=kx+b .
定义 直线l与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距.
方程是由直线的斜率k与它在y轴上的截距b确定,所以方程叫做直线的斜截式方程,简称斜截式.
l
说明:1.用斜截式方程表示直角坐标平面内的直线斜率必须存在.
2.截距与距离不一样,截距可正、可为零、可负, 而距离不能为负.
3.直线方程的斜截式即是一次函数.
新知探究
例3 求满足下列条件的m的值.
(1)直线l1:y=-x+1与直线l2:y=(m2-2)x+2m平行;
(2)直线l1:y=-2x+3与直线l2:y=(2m-1)x-5垂直.
典例精讲
巩固练习
巩固练习
巩固练习
注意:直线的点斜式,斜截式方程在直线斜率存在时才可以应用.
2.斜截式方程: y = kx +b
1.点斜式方程: y-y0=k(x-x0)
4.直线l1:y=k1x +b1,l2:y=k2x+b2
几何意义:k 是直线的斜率,b是直线在y轴上的截距
3.直线与x轴垂直时,倾斜角=90°
或
课堂小结
本课结束
