2.2.2 直线的两点式方程 课件(共21张PPT)
文档属性
| 名称 | 2.2.2 直线的两点式方程 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 594.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
2.2.2 直线的两点式方程
第二章 直线和圆的方程
新知探索
问题引入
已知直线l经过两点P1(x1,y1),P2(x2,y2)(x1≠x2,y1≠y2),因为两点确定一条直线,所以直线l是唯一确定的.也就是说,对于直线l上的任意一点P(x,y),它的坐标与点P1,P2的坐标之间具有唯一确定的关系.这一关系是什么呢?
新知探索
直线的两点式方程
当x1≠x2时,经过两点P1(x1,y1),P2(x2,y2)的直线的斜率为
任取P1,P2中的一点,例如取点P1(x1,y1),由直线的点斜式方程,得
当y1≠y2时,上式可写为
直线的两点式方程
新知探索
直线的两点式方程
即
可以变形为
不利用点斜式方程,你能求出两点式方程吗?
直线l上的任意一点P(x,y),
点P不与P1重合时
点P1的坐标(x1,y1)也满足上面的方程.
新知探索
直线的两点式方程
在P1(x1,y1),P2(x2,y2)中,如果x1=x2或y1=y2,则直线P1P2没有两点式方程.
当x1=x2时,直线P1P2垂直于x轴,直线方程为
即x=x1.
当y1=y2时,直线P1P2垂直于y轴,直线方程为
即y=y1.
新知探索
直线的两点式方程
P1(x1,y1),
P2(x2,y2).
直线不与坐标轴垂直时,可以用直线的两点式方程.
新知探索
直线的截距式方程
已知直线l与x轴的交点为A(a,0),与y轴的交点B(0,b),其中a≠0,b≠0.求直线l的方程.
解:将两点A(a,0),B(0,b)的坐标代入两点式,得
直线l与x轴的交点(a,0)的横坐标a叫做直线在x轴上截距.
直线的截距式方程.
即:
新知探索
直线的截距式方程
在y轴上的截距为b,且平行于x轴的直线方程为y=b;
注意直线过原点或与坐标轴平行时,没有截距式方程.此时直线的方程分别是什么?
在x轴上的截距为a,且平行于y轴的直线方程为x=a;
过原点(不与坐标轴重合)的直线的方程为y=kx(k≠0),这样的直线在两坐标轴上的截距都等于0.
新知探索
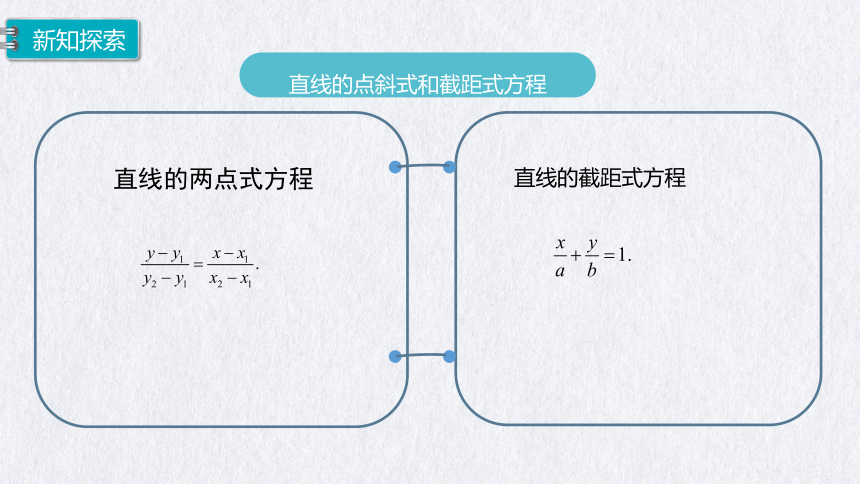
直线的点斜式和截距式方程
直线的两点式方程
直线的截距式方程
典例精析
题型一:用两点式求直线的方程
例1 求经过两点 P1(2,1),P2(0,3)的直线的两点式方程.
y
1
2
3
4
x
O
-1
2
l
解:将两点P1(2,1),P2(0,3)的坐标代入两点式,得
习惯上,将直线方程化为等号右边为0的形式:
典例精析
题型二:两点式的应用
例2 已知△ABC的三个顶点A(-5,0),B(3,-3),C(0,2),求边BC所在直线的方程,以及这条边上的中线AM所在直线的方程.
解:过B(3,-3),C(0,2)的两点式方程为
整理得
就是边BC所在直线的方程.
边BC上的中线是顶点A与边BC中点M所连线段, 由中点坐标公式,可得点M的坐标为:
即
过A(-5,0),M 两点的直线方程为
整理得
这就是边BC上中线AM所在直线的方程.
新知探索
归纳总结
两点式方程是点斜式方程的“变式”表达或推论,变化的依据是两点确定一条直线可以转化为一点和斜率唯一确定一条直线,而斜率可以由过这两个已知点的坐标求得.转化的关键是处理直线上任意一点的坐标(x,y)与两个已知点P1,P2的坐标之间的关系,从而建立直线的两点式方程.在两点式方程中,截距式方程是其特例,其特别之处在于这两点是直线与两条坐标轴的交点,它在具体问题中应用广泛.
典例精析
题型三:直线的截距式
答案:D
所以直线方程为x-y+1=0.
综上,所求直线方程为2x-y=0或x-y+1=0.故选D.
所以直线方程为y=2x,即2x-y=0,
例3 过点A(1,2)的直线在两坐标轴上的截距之和为0,则该直线方程为( )
A.x-y+1=0 B.x+y-3=0
C.2x-y=0或x+y-3=0 D.2x-y=0或x-y+1=0
解析:当直线过原点时,可得斜率为
当直线不过原点时,设方程为
代入点(1,2)可得
解得a=-1,
典例精析
题型四:直线的两点式截距式应用
例4 一条光线从点P(6,4)射出,与x轴相交于点Q(2,0),经x轴反射,求入射光线和反射光线所在直线的方程.
这就是入射光线所在直线的方程.
解:将点P(6,4),Q(2,0)的坐标代入两点式,得
化简为 ,
如图,由于光线经x轴反射,反射光线所在直线与入射光线所在直线关于x轴对称,点P关于x轴的对称点P'(6,-4),则反射光线所在直线即直线P'Q.
典例精析
题型四:直线的两点式截距式应用
例4 一条光线从点P(6,4)射出,与x轴相交于点Q(2,0),经x轴反射,求入射光线和反射光线所在直线的方程.
如图,由于入射角等于反射角,反射光线所在直线的倾斜角与入射光线所在直线的倾斜角互补,它们的斜率互为相反数.
反射光线所在直线的方程为
化简为
P'(6,-4),Q(2,0)代入两点式,得:
典例精析
题型四:直线的两点式截距式综合
例5 已知△ABC的三个顶点分别为A(0,4),B(-2,6),C(-8,0).
(1)求边AC和AB所在直线的方程;(2)求AC边上的中线BD所在直线的方程;
解:(1)由截距式,得边AC所在直线的方程为
即x-2y+8=0.
由两点式,得边AB所在直线的方程为
即x+y-4=0.
(2)由题意,得点D的坐标为(-4,2),由两点式,得BD所在直线的方程为
即2x-y+10=0.
跟踪练习
1.若点P (3, m)在过点 A (2, -1),B (-3, 4)的直线上,则m=_____
解:由直线方程的两点式得
∴直线 AB 的方程为 y+1=-x+2.
∵点 P (3, m) 在直线 AB上,
则 m+1=-3+2,
得 m=-2.
跟踪练习
2.求过定点 P (2, 3)且在两坐标轴上的截距相等的直线 l 的方程.
解:设直线的两截距都是a,则有
①当 a=0时,
直线设为 y=kx,
将P (2, 3) 代入得 ,
∴直线 l 的方程为 3x-2y=0.
②当 a ≠ 0时,
直线设为 ,
即 x+y=a,
把 P (2, 3)代入得 a=5,
∴直线 l 的方程为 x+y=5.
∴直线 l 的方程为 3x-2y=0 或 x+y-5=0.
跟踪练习
3.过点 P (3,0) 作直线 l,使它被两条相交直线2x-y-2 = 0和 x+y+3=0 所截得的线段 AB 恰好被P 点平分,求直线 l 的方程.
解:设直线 l 与直线 2x-y-2=0 交于点 A(x1,y1).
∵点P (3,0) 是线段AB 的中点,由中点坐标公式得B 点的坐标为(6-x1,-y1),
∴
解得 .
由两点式直线方程得直线 l 的方程为
即 8x―y―24=0.
跟踪练习
4.已知一个等腰三角形,两腰长是5,底边长是8,建立适当坐标系,求两腰所在的直线的方程.
解:以底边BC所在的直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系,易知点B,C的坐标分别为(-4,0),(4,0)
在Rt△AOC中,AC=5,OC=4,则OA=3.所以点A的坐标为(0,3).
即3x-4y+12=0;
即3x+4y-12=0
由直线的截距式方程得腰AB所在的直线方程为:
腰AC所在的直线方程为:
x
y
O
C
B
A
课堂小结
2.2.2 直线的两点式方程
第二章 直线和圆的方程
新知探索
问题引入
已知直线l经过两点P1(x1,y1),P2(x2,y2)(x1≠x2,y1≠y2),因为两点确定一条直线,所以直线l是唯一确定的.也就是说,对于直线l上的任意一点P(x,y),它的坐标与点P1,P2的坐标之间具有唯一确定的关系.这一关系是什么呢?
新知探索
直线的两点式方程
当x1≠x2时,经过两点P1(x1,y1),P2(x2,y2)的直线的斜率为
任取P1,P2中的一点,例如取点P1(x1,y1),由直线的点斜式方程,得
当y1≠y2时,上式可写为
直线的两点式方程
新知探索
直线的两点式方程
即
可以变形为
不利用点斜式方程,你能求出两点式方程吗?
直线l上的任意一点P(x,y),
点P不与P1重合时
点P1的坐标(x1,y1)也满足上面的方程.
新知探索
直线的两点式方程
在P1(x1,y1),P2(x2,y2)中,如果x1=x2或y1=y2,则直线P1P2没有两点式方程.
当x1=x2时,直线P1P2垂直于x轴,直线方程为
即x=x1.
当y1=y2时,直线P1P2垂直于y轴,直线方程为
即y=y1.
新知探索
直线的两点式方程
P1(x1,y1),
P2(x2,y2).
直线不与坐标轴垂直时,可以用直线的两点式方程.
新知探索
直线的截距式方程
已知直线l与x轴的交点为A(a,0),与y轴的交点B(0,b),其中a≠0,b≠0.求直线l的方程.
解:将两点A(a,0),B(0,b)的坐标代入两点式,得
直线l与x轴的交点(a,0)的横坐标a叫做直线在x轴上截距.
直线的截距式方程.
即:
新知探索
直线的截距式方程
在y轴上的截距为b,且平行于x轴的直线方程为y=b;
注意直线过原点或与坐标轴平行时,没有截距式方程.此时直线的方程分别是什么?
在x轴上的截距为a,且平行于y轴的直线方程为x=a;
过原点(不与坐标轴重合)的直线的方程为y=kx(k≠0),这样的直线在两坐标轴上的截距都等于0.
新知探索
直线的点斜式和截距式方程
直线的两点式方程
直线的截距式方程
典例精析
题型一:用两点式求直线的方程
例1 求经过两点 P1(2,1),P2(0,3)的直线的两点式方程.
y
1
2
3
4
x
O
-1
2
l
解:将两点P1(2,1),P2(0,3)的坐标代入两点式,得
习惯上,将直线方程化为等号右边为0的形式:
典例精析
题型二:两点式的应用
例2 已知△ABC的三个顶点A(-5,0),B(3,-3),C(0,2),求边BC所在直线的方程,以及这条边上的中线AM所在直线的方程.
解:过B(3,-3),C(0,2)的两点式方程为
整理得
就是边BC所在直线的方程.
边BC上的中线是顶点A与边BC中点M所连线段, 由中点坐标公式,可得点M的坐标为:
即
过A(-5,0),M 两点的直线方程为
整理得
这就是边BC上中线AM所在直线的方程.
新知探索
归纳总结
两点式方程是点斜式方程的“变式”表达或推论,变化的依据是两点确定一条直线可以转化为一点和斜率唯一确定一条直线,而斜率可以由过这两个已知点的坐标求得.转化的关键是处理直线上任意一点的坐标(x,y)与两个已知点P1,P2的坐标之间的关系,从而建立直线的两点式方程.在两点式方程中,截距式方程是其特例,其特别之处在于这两点是直线与两条坐标轴的交点,它在具体问题中应用广泛.
典例精析
题型三:直线的截距式
答案:D
所以直线方程为x-y+1=0.
综上,所求直线方程为2x-y=0或x-y+1=0.故选D.
所以直线方程为y=2x,即2x-y=0,
例3 过点A(1,2)的直线在两坐标轴上的截距之和为0,则该直线方程为( )
A.x-y+1=0 B.x+y-3=0
C.2x-y=0或x+y-3=0 D.2x-y=0或x-y+1=0
解析:当直线过原点时,可得斜率为
当直线不过原点时,设方程为
代入点(1,2)可得
解得a=-1,
典例精析
题型四:直线的两点式截距式应用
例4 一条光线从点P(6,4)射出,与x轴相交于点Q(2,0),经x轴反射,求入射光线和反射光线所在直线的方程.
这就是入射光线所在直线的方程.
解:将点P(6,4),Q(2,0)的坐标代入两点式,得
化简为 ,
如图,由于光线经x轴反射,反射光线所在直线与入射光线所在直线关于x轴对称,点P关于x轴的对称点P'(6,-4),则反射光线所在直线即直线P'Q.
典例精析
题型四:直线的两点式截距式应用
例4 一条光线从点P(6,4)射出,与x轴相交于点Q(2,0),经x轴反射,求入射光线和反射光线所在直线的方程.
如图,由于入射角等于反射角,反射光线所在直线的倾斜角与入射光线所在直线的倾斜角互补,它们的斜率互为相反数.
反射光线所在直线的方程为
化简为
P'(6,-4),Q(2,0)代入两点式,得:
典例精析
题型四:直线的两点式截距式综合
例5 已知△ABC的三个顶点分别为A(0,4),B(-2,6),C(-8,0).
(1)求边AC和AB所在直线的方程;(2)求AC边上的中线BD所在直线的方程;
解:(1)由截距式,得边AC所在直线的方程为
即x-2y+8=0.
由两点式,得边AB所在直线的方程为
即x+y-4=0.
(2)由题意,得点D的坐标为(-4,2),由两点式,得BD所在直线的方程为
即2x-y+10=0.
跟踪练习
1.若点P (3, m)在过点 A (2, -1),B (-3, 4)的直线上,则m=_____
解:由直线方程的两点式得
∴直线 AB 的方程为 y+1=-x+2.
∵点 P (3, m) 在直线 AB上,
则 m+1=-3+2,
得 m=-2.
跟踪练习
2.求过定点 P (2, 3)且在两坐标轴上的截距相等的直线 l 的方程.
解:设直线的两截距都是a,则有
①当 a=0时,
直线设为 y=kx,
将P (2, 3) 代入得 ,
∴直线 l 的方程为 3x-2y=0.
②当 a ≠ 0时,
直线设为 ,
即 x+y=a,
把 P (2, 3)代入得 a=5,
∴直线 l 的方程为 x+y=5.
∴直线 l 的方程为 3x-2y=0 或 x+y-5=0.
跟踪练习
3.过点 P (3,0) 作直线 l,使它被两条相交直线2x-y-2 = 0和 x+y+3=0 所截得的线段 AB 恰好被P 点平分,求直线 l 的方程.
解:设直线 l 与直线 2x-y-2=0 交于点 A(x1,y1).
∵点P (3,0) 是线段AB 的中点,由中点坐标公式得B 点的坐标为(6-x1,-y1),
∴
解得 .
由两点式直线方程得直线 l 的方程为
即 8x―y―24=0.
跟踪练习
4.已知一个等腰三角形,两腰长是5,底边长是8,建立适当坐标系,求两腰所在的直线的方程.
解:以底边BC所在的直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系,易知点B,C的坐标分别为(-4,0),(4,0)
在Rt△AOC中,AC=5,OC=4,则OA=3.所以点A的坐标为(0,3).
即3x-4y+12=0;
即3x+4y-12=0
由直线的截距式方程得腰AB所在的直线方程为:
腰AC所在的直线方程为:
x
y
O
C
B
A
课堂小结
