2.4.2圆的一般方程 课件(共22张PPT)
文档属性
| 名称 | 2.4.2圆的一般方程 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 567.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 17:10:29 | ||
图片预览







文档简介
(共22张PPT)
2.4.2 圆的一般方程
第二章 直线和圆的方程
学习目标
学习目标
1.了解圆的一般方程的特点,会由一般方程求圆心和半径.(重点)
2.会根据给定的条件求圆的一般方程,并能用圆的一般方程解决简单问题.(重点)
3.灵活选取恰当的方法求圆的方程.(难点)
核心素养
1.通过圆的一般方程的学习,培养数学抽象的核心素养.
2.借助圆的一般方程的求解及其应用,培养数学运算的数学核心素养.
问题引入
圆的一般方程
我们已经学习了曲线与方程的关系,也已经认识了直线方程的多种形式,刚刚学习了圆的标准方程,现给出一个二元二次方程:x2+y2+Dx+Ey+F=0(D,E,F为常数),请问这个方程在什么条件下是一个圆的方程
新知探索
圆的一般方程
1.圆的一般方程
一般地,如果平面直角坐标系中☉C的圆心为C(a,b),半径为r(r>0),则圆的标准方程为
展开化简:
即
令
则
这就是圆的一般方程,满足的条件为:
新知探索
圆的一般方程
圆的标准方程为:
即:
化为标准方程:
所以必须满足:
圆的方程为 时,它的圆心:
半径为:
新知探索
圆的一般方程的说明
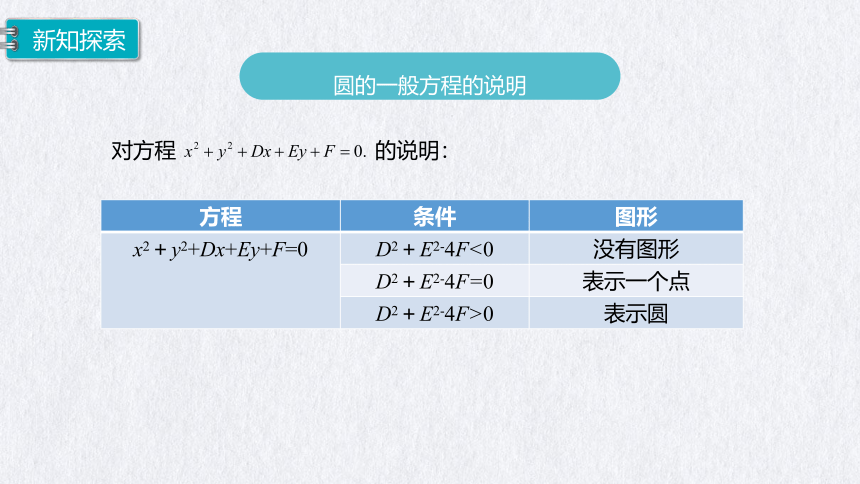
方程 条件 图形
x2+y2+Dx+Ey+F=0 D2+E2-4F<0 没有图形
D2+E2-4F=0 表示一个点
D2+E2-4F>0 表示圆
对方程 的说明:
新知探索
圆的一般方程的特征
思考1:圆的标准方程与圆的一般方程有什么不同?
思考2:求圆的一般方程实质上是求圆的一般方程中的哪些量?
只要求出一般方程中的D、E、F圆的方程就确定了.
圆的一般方程是一种特殊的二元二次方程,代数特征明显.圆的标准方程则指出了圆心坐标与半径大小,几何特征明显.
思考3:所有二元二次方程均表示圆吗?
不是,Ax2+Bxy+Cy2+Dx+Ey+F=0,只有在A=C≠0,B=0且D2+E2-4AF>0时才表示圆.
[答案] (1)√ (2)√ (3)×
小试身手
1.思考辨析(正确的打“√”,错误的打“×”)
(1)任何一个圆的方程都能写为一个二元二次方程. ( )
(2)圆的一般方程和标准方程可以互化. ( )
(3)方程 表示圆心为 ,半径
为 的圆.
(1)正确.圆的方程都能写成一个二元二次方程.
(2)正确.圆的一般方程和标准方程是可以互化的.
(3)错误.当 ,即 时才表示圆.
典例精析
题型一:圆的一般方程的概念
例1.若方程x2+y2+2mx-2y+m2+5m=0表示圆,求:
(1)实数m的取值范围;
(2)圆心坐标和半径.
写成(x+m)2+(y-1)2=1-5m.
(2)将方程x2+y2+2mx-2y+m2+5m=0
解:(1)据题意知
即
解得:
故m的取值范围为
故圆心坐标为(-m,1),半径
规律方法
题型一:圆的一般方程的判断
形如 的二元二次方程,判定其是否表示圆时可有如下两种方法:
1.由圆的一般方程的定义令 ,成立则表示圆,否则不表示圆.
2.将方程配方后,根据圆的标准方程的特征求解.
典例精析
题型二:求圆的一般方程
例2 .圆C过点A(1,2),B(3,4),且在x轴上截得的弦长为6,求圆C的方程.
解:设所求圆的方程为
∵圆过A(1,2),B(3,4),
∴D+2E+F=-5,①
3D+4E+F=-25.②
令y=0,得
设圆C与x轴的两个交点的横坐标为
则
即D2-4F=36.③
由 ①②③得D=12,E=-22,F=27,
或D=-8,E=-2,F=7.
故所求圆的方程为x2+y2+12x-22y+27=0,或x2+y2-8x-2y+7=0.
规律方法
应用待定系数法求圆的方程
1.如果由已知条件容易求得圆心坐标、半径或需利用圆心的坐标或半径列方程的问题,一般采用圆的标准方程,再用待定系数法求出a,b,r;
2.如果已知条件与圆心和半径都无直接关系,一般采用圆的一般方程,再用待定系数法求出常数D,E,F.
题型二:待定系数法求圆的方程
典例精析
例3 .过点A(8,0)的直线与圆x2+y2=4交于点B,则AB中点P的轨迹方程为________.
题型三:与圆有关求动点的轨迹方程
解:设点P的坐标为(x,y),点B为 ,
由题意,结合中点坐标公式可得 ,故(2x-8)2+(2y)2=4,化简得(x-4)2+y2=1,则AB中点P的轨迹方程为(x-4)2+y2=1.
典例精析
例4 .已知Rt△ABC中,A(-1,0),B(3,0).求:直角顶点C的轨迹方程.
题型三:与圆有关求动点的轨迹方程
解:(1)方法一:(直接法)设C(x,y),
则
因为AC⊥BC,所以kAC·kBC=-1,
即
化简得x2+y2-2x-3=0.
由于A、B、C不共线,所以y≠0.
故顶点C的轨迹方程为x2+y2-2x-3=0(y≠0).
方法二:(定义法)设线段AB的中点为D,则D(1,0).
由题意知 .
所以点C的轨迹是以D为圆心,以2为半径的圆,其方程为(x-1)2+y2=4.
由于直角顶点C不在直线AB上,
所以y≠0.
故顶点C的轨迹方程为
x2+y2-2x-3=0(y≠0).
规律方法
题型三:求与圆有关的轨迹方法
求与圆有关的轨迹的方法
1.直接法:直接根据题目提供的条件列出方程;
2.定义法:根据圆、直线等定义列方程;
3.几何法:利用圆的几何性质列方程.
跟踪练习
解:圆的标准方程为(x-1)2+(y+2)2=5,
则圆心坐标为(1,-2),
∵直线2x+y+m=0过x2+y2-2x+4y=0的圆心.
∴2-2+m=0得m=0.故选D.
1.若直线2x+y+m=0过圆x2+y2-2x+4y=0的圆心,则m的值为( )
A.2 B.-1 C.-2 D.0
跟踪练习
2.(1)若方程x2+y2-4x+2y+5k=0表示圆,则实数k的取值范围是( )
A.(-∞,1) B.(1,+∞) C.(-∞,0) D.(-∞,1]
解析:(1)因为x2+y2-4x+2y+5k=0表示圆,
则16+4-4×5k>0,所以k<1.故选A.
(2)当圆C:x2+y2-4x-2my+2m=0的面积最小时,m的取值是( )
A.4 B.3 C.2 D.1
(2)∵圆C:x2+y2-4x-2my+2m=0,
∴圆C的标准方程为
(x-2)2+(y-m)2=m2-2m+4,
从而对于圆C的半径r有
r2=m2-2m+4=(m-1)2+3≥3,
所以当m=1时,r2取得最小值,
从而圆C的面积πr2在m=1时取得最小值.故选D.
跟踪练习
3.已知A(2,2),B(5,3),C(3,-1).
(1)求△ABC的外接圆的一般方程;
(2)若点M(a,2)在△ABC的外接圆上,求a的值.
解:(1)设△ABC外接圆的一般方程为x2+y2+Dx+Ey+F=0,
由题意,得
解得
∴△ABC外接圆的一般方程为
x2+y2-8x-2y+12=0,
跟踪练习
3.已知A(2,2),B(5,3),C(3,-1).
(1)求△ABC的外接圆的一般方程;
(2)若点M(a,2)在△ABC的外接圆上,求a的值.
解:(2)由(1)知,△ABC的外接圆的方程为x2+y2-8x-2y+12=0,
∵点M(a,2)在△ABC的外接圆上,
∴a2+22-8a-2×2+12=0,
即a2-8a+12=0,
解得a=2或6.
跟踪练习
4.已知点P在圆C:x2+y2-8x-6y+21=0上运动,求线段OP的中点M的轨迹方程.
解:设点M(x,y),点P(x0,y0),
则
所以,
所以(2x)2+(2y)2-8·(2x)-6·(2y)+21=0,
因为点P(x0,y0)在圆C:x2+y2-8x-6y+21=0上,
∴
即点M的轨迹方程为
课堂小结
本
课
结
束
2.4.2 圆的一般方程
第二章 直线和圆的方程
学习目标
学习目标
1.了解圆的一般方程的特点,会由一般方程求圆心和半径.(重点)
2.会根据给定的条件求圆的一般方程,并能用圆的一般方程解决简单问题.(重点)
3.灵活选取恰当的方法求圆的方程.(难点)
核心素养
1.通过圆的一般方程的学习,培养数学抽象的核心素养.
2.借助圆的一般方程的求解及其应用,培养数学运算的数学核心素养.
问题引入
圆的一般方程
我们已经学习了曲线与方程的关系,也已经认识了直线方程的多种形式,刚刚学习了圆的标准方程,现给出一个二元二次方程:x2+y2+Dx+Ey+F=0(D,E,F为常数),请问这个方程在什么条件下是一个圆的方程
新知探索
圆的一般方程
1.圆的一般方程
一般地,如果平面直角坐标系中☉C的圆心为C(a,b),半径为r(r>0),则圆的标准方程为
展开化简:
即
令
则
这就是圆的一般方程,满足的条件为:
新知探索
圆的一般方程
圆的标准方程为:
即:
化为标准方程:
所以必须满足:
圆的方程为 时,它的圆心:
半径为:
新知探索
圆的一般方程的说明
方程 条件 图形
x2+y2+Dx+Ey+F=0 D2+E2-4F<0 没有图形
D2+E2-4F=0 表示一个点
D2+E2-4F>0 表示圆
对方程 的说明:
新知探索
圆的一般方程的特征
思考1:圆的标准方程与圆的一般方程有什么不同?
思考2:求圆的一般方程实质上是求圆的一般方程中的哪些量?
只要求出一般方程中的D、E、F圆的方程就确定了.
圆的一般方程是一种特殊的二元二次方程,代数特征明显.圆的标准方程则指出了圆心坐标与半径大小,几何特征明显.
思考3:所有二元二次方程均表示圆吗?
不是,Ax2+Bxy+Cy2+Dx+Ey+F=0,只有在A=C≠0,B=0且D2+E2-4AF>0时才表示圆.
[答案] (1)√ (2)√ (3)×
小试身手
1.思考辨析(正确的打“√”,错误的打“×”)
(1)任何一个圆的方程都能写为一个二元二次方程. ( )
(2)圆的一般方程和标准方程可以互化. ( )
(3)方程 表示圆心为 ,半径
为 的圆.
(1)正确.圆的方程都能写成一个二元二次方程.
(2)正确.圆的一般方程和标准方程是可以互化的.
(3)错误.当 ,即 时才表示圆.
典例精析
题型一:圆的一般方程的概念
例1.若方程x2+y2+2mx-2y+m2+5m=0表示圆,求:
(1)实数m的取值范围;
(2)圆心坐标和半径.
写成(x+m)2+(y-1)2=1-5m.
(2)将方程x2+y2+2mx-2y+m2+5m=0
解:(1)据题意知
即
解得:
故m的取值范围为
故圆心坐标为(-m,1),半径
规律方法
题型一:圆的一般方程的判断
形如 的二元二次方程,判定其是否表示圆时可有如下两种方法:
1.由圆的一般方程的定义令 ,成立则表示圆,否则不表示圆.
2.将方程配方后,根据圆的标准方程的特征求解.
典例精析
题型二:求圆的一般方程
例2 .圆C过点A(1,2),B(3,4),且在x轴上截得的弦长为6,求圆C的方程.
解:设所求圆的方程为
∵圆过A(1,2),B(3,4),
∴D+2E+F=-5,①
3D+4E+F=-25.②
令y=0,得
设圆C与x轴的两个交点的横坐标为
则
即D2-4F=36.③
由 ①②③得D=12,E=-22,F=27,
或D=-8,E=-2,F=7.
故所求圆的方程为x2+y2+12x-22y+27=0,或x2+y2-8x-2y+7=0.
规律方法
应用待定系数法求圆的方程
1.如果由已知条件容易求得圆心坐标、半径或需利用圆心的坐标或半径列方程的问题,一般采用圆的标准方程,再用待定系数法求出a,b,r;
2.如果已知条件与圆心和半径都无直接关系,一般采用圆的一般方程,再用待定系数法求出常数D,E,F.
题型二:待定系数法求圆的方程
典例精析
例3 .过点A(8,0)的直线与圆x2+y2=4交于点B,则AB中点P的轨迹方程为________.
题型三:与圆有关求动点的轨迹方程
解:设点P的坐标为(x,y),点B为 ,
由题意,结合中点坐标公式可得 ,故(2x-8)2+(2y)2=4,化简得(x-4)2+y2=1,则AB中点P的轨迹方程为(x-4)2+y2=1.
典例精析
例4 .已知Rt△ABC中,A(-1,0),B(3,0).求:直角顶点C的轨迹方程.
题型三:与圆有关求动点的轨迹方程
解:(1)方法一:(直接法)设C(x,y),
则
因为AC⊥BC,所以kAC·kBC=-1,
即
化简得x2+y2-2x-3=0.
由于A、B、C不共线,所以y≠0.
故顶点C的轨迹方程为x2+y2-2x-3=0(y≠0).
方法二:(定义法)设线段AB的中点为D,则D(1,0).
由题意知 .
所以点C的轨迹是以D为圆心,以2为半径的圆,其方程为(x-1)2+y2=4.
由于直角顶点C不在直线AB上,
所以y≠0.
故顶点C的轨迹方程为
x2+y2-2x-3=0(y≠0).
规律方法
题型三:求与圆有关的轨迹方法
求与圆有关的轨迹的方法
1.直接法:直接根据题目提供的条件列出方程;
2.定义法:根据圆、直线等定义列方程;
3.几何法:利用圆的几何性质列方程.
跟踪练习
解:圆的标准方程为(x-1)2+(y+2)2=5,
则圆心坐标为(1,-2),
∵直线2x+y+m=0过x2+y2-2x+4y=0的圆心.
∴2-2+m=0得m=0.故选D.
1.若直线2x+y+m=0过圆x2+y2-2x+4y=0的圆心,则m的值为( )
A.2 B.-1 C.-2 D.0
跟踪练习
2.(1)若方程x2+y2-4x+2y+5k=0表示圆,则实数k的取值范围是( )
A.(-∞,1) B.(1,+∞) C.(-∞,0) D.(-∞,1]
解析:(1)因为x2+y2-4x+2y+5k=0表示圆,
则16+4-4×5k>0,所以k<1.故选A.
(2)当圆C:x2+y2-4x-2my+2m=0的面积最小时,m的取值是( )
A.4 B.3 C.2 D.1
(2)∵圆C:x2+y2-4x-2my+2m=0,
∴圆C的标准方程为
(x-2)2+(y-m)2=m2-2m+4,
从而对于圆C的半径r有
r2=m2-2m+4=(m-1)2+3≥3,
所以当m=1时,r2取得最小值,
从而圆C的面积πr2在m=1时取得最小值.故选D.
跟踪练习
3.已知A(2,2),B(5,3),C(3,-1).
(1)求△ABC的外接圆的一般方程;
(2)若点M(a,2)在△ABC的外接圆上,求a的值.
解:(1)设△ABC外接圆的一般方程为x2+y2+Dx+Ey+F=0,
由题意,得
解得
∴△ABC外接圆的一般方程为
x2+y2-8x-2y+12=0,
跟踪练习
3.已知A(2,2),B(5,3),C(3,-1).
(1)求△ABC的外接圆的一般方程;
(2)若点M(a,2)在△ABC的外接圆上,求a的值.
解:(2)由(1)知,△ABC的外接圆的方程为x2+y2-8x-2y+12=0,
∵点M(a,2)在△ABC的外接圆上,
∴a2+22-8a-2×2+12=0,
即a2-8a+12=0,
解得a=2或6.
跟踪练习
4.已知点P在圆C:x2+y2-8x-6y+21=0上运动,求线段OP的中点M的轨迹方程.
解:设点M(x,y),点P(x0,y0),
则
所以,
所以(2x)2+(2y)2-8·(2x)-6·(2y)+21=0,
因为点P(x0,y0)在圆C:x2+y2-8x-6y+21=0上,
∴
即点M的轨迹方程为
课堂小结
本
课
结
束
