2.5.1 第1课时 直线与圆的位置关系 课件(共25张PPT)
文档属性
| 名称 | 2.5.1 第1课时 直线与圆的位置关系 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 575.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 17:10:52 | ||
图片预览






文档简介
(共25张PPT)
2.5.1 第1课时 直线与圆的位置关系
第二章 直线和圆的方程
学习目标
学习目标
1.理解直线与圆的三种位置关系.
(重点)
2.会用代数法和几何法判断直线与圆的位置关系.(重点)
3.能解决直线与圆位置关系的综合问题.(难点)
核心素养
1.通过直线与圆的位置关系的学习,培养直观想象逻辑推理的数学核心素养.
2.通过解决直线与圆位置关系的综合问题,培养数学运算的核心素养.
问题引入
直线与圆的位置关系
早晨的日出非常美丽,如果我们把海平面看成一条直线,而把太阳抽象成一个运动着的圆,观察太阳缓缓升起的这样一个过程.你能想象到什么几何知识呢?没错,日出升起的过程可以体现直线与圆的三种特殊位置关系.你发现了吗?
新知探索
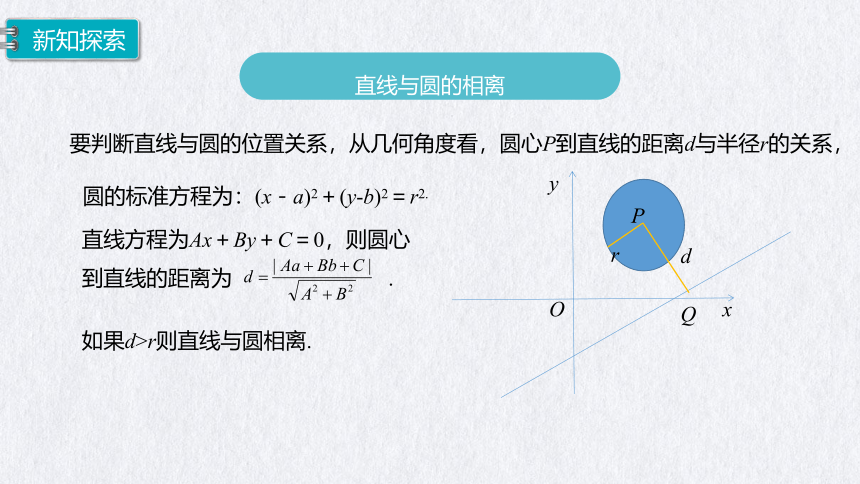
直线与圆的相离
要判断直线与圆的位置关系,从几何角度看,圆心P到直线的距离d与半径r的关系,
P
x
y
Q
O
d
r
圆的标准方程为:(x-a)2+(y-b)2=r2.
直线方程为Ax+By+C=0,则圆心到直线的距离为 .
如果d>r则直线与圆相离.
新知探索
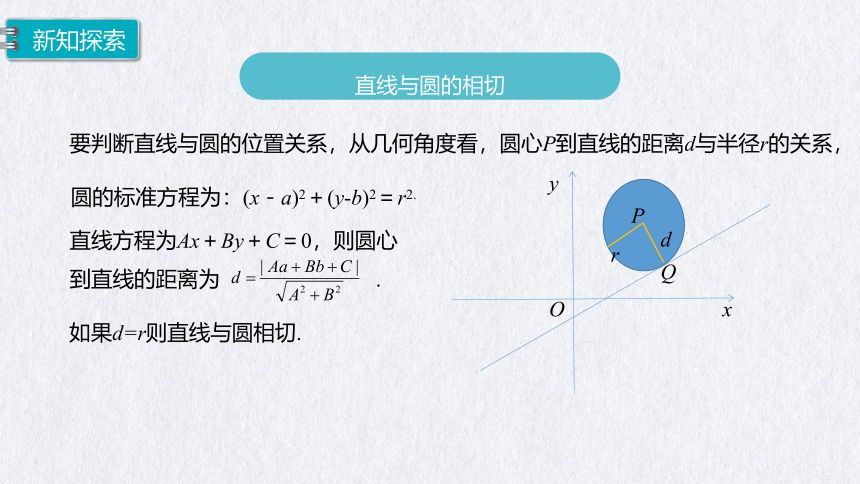
直线与圆的相切
要判断直线与圆的位置关系,从几何角度看,圆心P到直线的距离d与半径r的关系,
P
x
y
Q
O
d
r
圆的标准方程为:(x-a)2+(y-b)2=r2.
直线方程为Ax+By+C=0,则圆心到直线的距离为 .
如果d=r则直线与圆相切.
新知探索
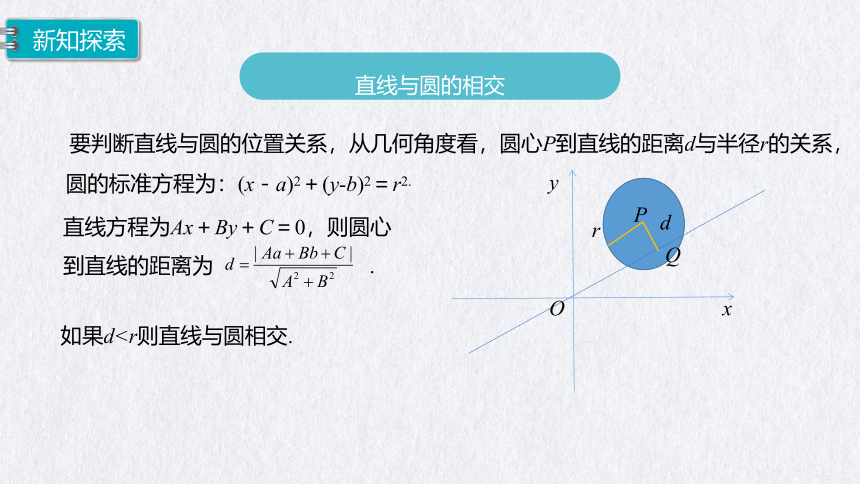
直线与圆的相交
要判断直线与圆的位置关系,从几何角度看,圆心P到直线的距离d与半径r的关系,
P
x
y
Q
O
d
r
圆的标准方程为:(x-a)2+(y-b)2=r2.
直线方程为Ax+By+C=0,则圆心到直线的距离为 .
如果d新知探索
代数法判断直线与圆的位置关系
圆的标准方程为:(x-a)2+(y-b)2=r2,
直线方程为Ax+By+C=0,联立直线与圆的方程:
得到一元二次方程,由判别式确定直线与圆的位置关系.
新知探索
代数法判断直线与圆的位置关系
得到一元二次方程,由判别式 确定直线与圆的位置关系.
如果
Δ>0,对应的一元二次方程有两不等实根,直线与圆相交
如果
如果
Δ=0,对应的一元二次方程有两相等实根,直线与圆相切
Δ<0,对应的一元二次方程无解,直线与圆相离
小试身手
[答案] (1)√ (2)√
1.思考辨析(正确的打“√”,错误的打“×”)
(1)如果直线与圆组成的方程组有解,则直线与圆相交或相切.( )
(2)若直线与圆只有一个公共点,则直线与圆一定相切. ( )
小试身手
2.直线x+y=1与圆x2+y2-2ay=0(a>0)没有公共点,则a的取值范围是 .
由题意得圆心(0,a)到直线x+y-1=0的距离大于半径a,即
解得 ,又a>0,∴
典例精析
题型一:直线与圆的位置关系判定
例1.已知直线y=x+b与圆x2+y2=2,当b为何值时,圆与直线有两个公共点?只有一个公共点?没有公共点?
(1)当-2<b<2时,Δ>0,直线与圆有两个公共点.
(2)当b=2或b=-2时,Δ=0,直线与圆只有一个公共点.
(3)当b<-2或b>2时,Δ<0方程组没有实数解,直线与圆没有公共点.
解:法一:据题意知
得
判别式
典例精析
题型一:直线与圆的位置关系判定
例1.已知直线y=x+b与圆x2+y2=2,当b为何值时,圆与直线有两个公共点?只有一个公共点?没有公共点?
当d=r,|b|=2,即b=2或b=-2时,圆与直线相切,直线与圆只有一个公共点.
当d>r,|b|>2,即b<-2或b>2时,圆与直线相离,圆与直线无公共点.
解:法二:圆的半径 ,圆心O(0,0)到直线y=x+b的距离为 .
当d<r,即-2<b<2时,圆与直线相交,有两个公共点.
规律方法
直线与圆的位置关系的判断方法
(1)几何法:由圆心到直线的距离d与圆的半径r的大小关系判断.
(2)代数法:根据直线方程与圆的方程组成的方程组解的个数来判断.
题型一:直线与圆的位置关系的判断
典例精析
题型二:直线系与圆的位置关系
解:∵直线l:x+my+3m=0可化为
x+m(y+3)m=0,
∴直线恒过定点(0,-3).
∴点(0,-3)在圆内.
而直线l恒过定点(0,-3),
所以,直线与圆相交.
例2 .若直线l:x+my+3m=0,圆C:(x+1)2+(y+2)2=16,判断直线与圆的位置关系.
(0+1)2+(-3+2)2=2<16.
规律方法
直线系法:若直线恒过定点,可通过判断点与圆的位置关系来判断直线与圆的位置关系,但有一定的局限性,必须是过定点的直线系.
题型二:直线系与圆的位置关系
典例精析
例3 .过点A(4,-3)作圆C:(x-3)2+(y-1)2=1的切线,求此切线的方程.
题型三:直线与圆的相切
解:因为(4-3)2+(-3-1)2=17>1,
所以点A在圆外.
(1)若所求切线的斜率存在,设切线斜率为k,
则切线方程为y+3=k(x-4).
因为圆心C(3,1)到切线的距离等于半径,
半径为1,
所以 ,即
所以k2+8k+16=k2+1,解得
所以切线方程为y+3= (x-4),
即15x+8y-36=0.
(2)若直线斜率不存在,
圆心C(3,1)到直线x=4的距离为1,
这时直线与圆相切,所以另一条切线方程是x=4.
综上,所求切线方程为
15x+8y-36=0或x=4.
规律方法
题型三:直线与圆相切
(2)点在圆外时
几何法:设切线方程为y-y0=k(x-x0).由圆心到直线的距离等于半径,可求得k,也就得切线方程.
代数法:设切线方程为y-y0=k(x-x0),与圆的方程联立,消去y后得到关于x的一元二次方程,由Δ=0求出k,可得切线方程.
过一点的圆的切线方程的求法
(1)点在圆上时,求过圆上一点(x0,y0)的圆的切线方程:先求切点与圆心连线的斜率k,再由垂直关系得切线的斜率为 ,由点斜式可得切线方程.如果斜率为零或不存在,则由图形可直接得切线方程x=x0或y=y0.
典例精析
例4.已知点 均在圆C上.(1)求圆C的方程;
(2)若直线3x-y+1=0与圆C相交于A,B两点,求线段AB的长.
题型四:弦长问题
∴圆C的方程为(x-1)2+(y+2)2=9.
解:(1)∵点
均在圆C上,
∴圆心C的横坐标为1,设圆C的方程为(x-1)2+(y-b)2=r2,
则 解得
(2)圆C的圆心坐标为(1,-2),半径为3,
圆心到直线3x-y+1=0的距离为
∴直线3x-y+1=0被圆C截得的弦AB的长为
规律方法
弦长问题
直线与圆相交时弦长的两种求法
1.几何法:直线l与圆C交于A,B两点,设弦心距为d,圆的半径为r,弦长为|AB|,则有 ,则
2.代数法:将直线方程与圆的方程联立,设直线与圆的两交点分别是
,则
(直线l的斜率k存在且不为0).
跟踪练习
1.直线x+y=1与圆x2+y2-2ay=0(a>0)没有公共点,则a的取值范围是___________.
解:由题意得圆心(0,a)到直线x+y-1=0的距离大于半径a,即
解得
又a>0,∴
因此,a的取值范围是
跟踪练习
2.对任意的实数k,直线y=kx+1与圆x2+y2=2的位置关系一定是( )
A.相离 B.相切
C.相交但直线不过圆心 D.相交且直线过圆心
解:直线y=kx+1恒过定点(0,1),由定点(0,1)在圆x2+y2=2内,知直线y=kx+1与圆x2+y2=2一定相交.又直线y=kx+1不过圆心(0,0),
则位置关系是相交但直线不过圆心,故选C.
C
跟踪练习
3.直线y=x-1上的点与圆x2+y2+4x-2y+4=0上的点的距离的最小值为( )
A. B. C. D.1
解:圆x2+y2+4x-2y+4=0的圆心为(-2,1),半径为1,圆心到直线y=x-1的距离为
所以 直线y=x-1上的点与圆x2+y2+4x-2y+4=0上的点的距离的最小值为 .
C
跟踪练习
4.已知直线l:mx+y-3=0与圆(x-1)2+(y-2)2=4交于A,B两点,过A,B分别做l的垂线与x轴交于C,D两点,若|AB|=4,则|CD|= .
解:圆(x-1)2+(y-2)2=4,圆心(1,2),半径r=2,
∵|AB|=4,∴直线l:mx+y-3=0过圆心(1,2),
∴m+2-3=0,∴m=1,
∴直线l:x+y-3=0,倾斜角为135°,
∵过A,B分别做l的垂线与x轴交于C,D两点,
课堂小结
本
课
结
束
2.5.1 第1课时 直线与圆的位置关系
第二章 直线和圆的方程
学习目标
学习目标
1.理解直线与圆的三种位置关系.
(重点)
2.会用代数法和几何法判断直线与圆的位置关系.(重点)
3.能解决直线与圆位置关系的综合问题.(难点)
核心素养
1.通过直线与圆的位置关系的学习,培养直观想象逻辑推理的数学核心素养.
2.通过解决直线与圆位置关系的综合问题,培养数学运算的核心素养.
问题引入
直线与圆的位置关系
早晨的日出非常美丽,如果我们把海平面看成一条直线,而把太阳抽象成一个运动着的圆,观察太阳缓缓升起的这样一个过程.你能想象到什么几何知识呢?没错,日出升起的过程可以体现直线与圆的三种特殊位置关系.你发现了吗?
新知探索
直线与圆的相离
要判断直线与圆的位置关系,从几何角度看,圆心P到直线的距离d与半径r的关系,
P
x
y
Q
O
d
r
圆的标准方程为:(x-a)2+(y-b)2=r2.
直线方程为Ax+By+C=0,则圆心到直线的距离为 .
如果d>r则直线与圆相离.
新知探索
直线与圆的相切
要判断直线与圆的位置关系,从几何角度看,圆心P到直线的距离d与半径r的关系,
P
x
y
Q
O
d
r
圆的标准方程为:(x-a)2+(y-b)2=r2.
直线方程为Ax+By+C=0,则圆心到直线的距离为 .
如果d=r则直线与圆相切.
新知探索
直线与圆的相交
要判断直线与圆的位置关系,从几何角度看,圆心P到直线的距离d与半径r的关系,
P
x
y
Q
O
d
r
圆的标准方程为:(x-a)2+(y-b)2=r2.
直线方程为Ax+By+C=0,则圆心到直线的距离为 .
如果d
代数法判断直线与圆的位置关系
圆的标准方程为:(x-a)2+(y-b)2=r2,
直线方程为Ax+By+C=0,联立直线与圆的方程:
得到一元二次方程,由判别式确定直线与圆的位置关系.
新知探索
代数法判断直线与圆的位置关系
得到一元二次方程,由判别式 确定直线与圆的位置关系.
如果
Δ>0,对应的一元二次方程有两不等实根,直线与圆相交
如果
如果
Δ=0,对应的一元二次方程有两相等实根,直线与圆相切
Δ<0,对应的一元二次方程无解,直线与圆相离
小试身手
[答案] (1)√ (2)√
1.思考辨析(正确的打“√”,错误的打“×”)
(1)如果直线与圆组成的方程组有解,则直线与圆相交或相切.( )
(2)若直线与圆只有一个公共点,则直线与圆一定相切. ( )
小试身手
2.直线x+y=1与圆x2+y2-2ay=0(a>0)没有公共点,则a的取值范围是 .
由题意得圆心(0,a)到直线x+y-1=0的距离大于半径a,即
解得 ,又a>0,∴
典例精析
题型一:直线与圆的位置关系判定
例1.已知直线y=x+b与圆x2+y2=2,当b为何值时,圆与直线有两个公共点?只有一个公共点?没有公共点?
(1)当-2<b<2时,Δ>0,直线与圆有两个公共点.
(2)当b=2或b=-2时,Δ=0,直线与圆只有一个公共点.
(3)当b<-2或b>2时,Δ<0方程组没有实数解,直线与圆没有公共点.
解:法一:据题意知
得
判别式
典例精析
题型一:直线与圆的位置关系判定
例1.已知直线y=x+b与圆x2+y2=2,当b为何值时,圆与直线有两个公共点?只有一个公共点?没有公共点?
当d=r,|b|=2,即b=2或b=-2时,圆与直线相切,直线与圆只有一个公共点.
当d>r,|b|>2,即b<-2或b>2时,圆与直线相离,圆与直线无公共点.
解:法二:圆的半径 ,圆心O(0,0)到直线y=x+b的距离为 .
当d<r,即-2<b<2时,圆与直线相交,有两个公共点.
规律方法
直线与圆的位置关系的判断方法
(1)几何法:由圆心到直线的距离d与圆的半径r的大小关系判断.
(2)代数法:根据直线方程与圆的方程组成的方程组解的个数来判断.
题型一:直线与圆的位置关系的判断
典例精析
题型二:直线系与圆的位置关系
解:∵直线l:x+my+3m=0可化为
x+m(y+3)m=0,
∴直线恒过定点(0,-3).
∴点(0,-3)在圆内.
而直线l恒过定点(0,-3),
所以,直线与圆相交.
例2 .若直线l:x+my+3m=0,圆C:(x+1)2+(y+2)2=16,判断直线与圆的位置关系.
(0+1)2+(-3+2)2=2<16.
规律方法
直线系法:若直线恒过定点,可通过判断点与圆的位置关系来判断直线与圆的位置关系,但有一定的局限性,必须是过定点的直线系.
题型二:直线系与圆的位置关系
典例精析
例3 .过点A(4,-3)作圆C:(x-3)2+(y-1)2=1的切线,求此切线的方程.
题型三:直线与圆的相切
解:因为(4-3)2+(-3-1)2=17>1,
所以点A在圆外.
(1)若所求切线的斜率存在,设切线斜率为k,
则切线方程为y+3=k(x-4).
因为圆心C(3,1)到切线的距离等于半径,
半径为1,
所以 ,即
所以k2+8k+16=k2+1,解得
所以切线方程为y+3= (x-4),
即15x+8y-36=0.
(2)若直线斜率不存在,
圆心C(3,1)到直线x=4的距离为1,
这时直线与圆相切,所以另一条切线方程是x=4.
综上,所求切线方程为
15x+8y-36=0或x=4.
规律方法
题型三:直线与圆相切
(2)点在圆外时
几何法:设切线方程为y-y0=k(x-x0).由圆心到直线的距离等于半径,可求得k,也就得切线方程.
代数法:设切线方程为y-y0=k(x-x0),与圆的方程联立,消去y后得到关于x的一元二次方程,由Δ=0求出k,可得切线方程.
过一点的圆的切线方程的求法
(1)点在圆上时,求过圆上一点(x0,y0)的圆的切线方程:先求切点与圆心连线的斜率k,再由垂直关系得切线的斜率为 ,由点斜式可得切线方程.如果斜率为零或不存在,则由图形可直接得切线方程x=x0或y=y0.
典例精析
例4.已知点 均在圆C上.(1)求圆C的方程;
(2)若直线3x-y+1=0与圆C相交于A,B两点,求线段AB的长.
题型四:弦长问题
∴圆C的方程为(x-1)2+(y+2)2=9.
解:(1)∵点
均在圆C上,
∴圆心C的横坐标为1,设圆C的方程为(x-1)2+(y-b)2=r2,
则 解得
(2)圆C的圆心坐标为(1,-2),半径为3,
圆心到直线3x-y+1=0的距离为
∴直线3x-y+1=0被圆C截得的弦AB的长为
规律方法
弦长问题
直线与圆相交时弦长的两种求法
1.几何法:直线l与圆C交于A,B两点,设弦心距为d,圆的半径为r,弦长为|AB|,则有 ,则
2.代数法:将直线方程与圆的方程联立,设直线与圆的两交点分别是
,则
(直线l的斜率k存在且不为0).
跟踪练习
1.直线x+y=1与圆x2+y2-2ay=0(a>0)没有公共点,则a的取值范围是___________.
解:由题意得圆心(0,a)到直线x+y-1=0的距离大于半径a,即
解得
又a>0,∴
因此,a的取值范围是
跟踪练习
2.对任意的实数k,直线y=kx+1与圆x2+y2=2的位置关系一定是( )
A.相离 B.相切
C.相交但直线不过圆心 D.相交且直线过圆心
解:直线y=kx+1恒过定点(0,1),由定点(0,1)在圆x2+y2=2内,知直线y=kx+1与圆x2+y2=2一定相交.又直线y=kx+1不过圆心(0,0),
则位置关系是相交但直线不过圆心,故选C.
C
跟踪练习
3.直线y=x-1上的点与圆x2+y2+4x-2y+4=0上的点的距离的最小值为( )
A. B. C. D.1
解:圆x2+y2+4x-2y+4=0的圆心为(-2,1),半径为1,圆心到直线y=x-1的距离为
所以 直线y=x-1上的点与圆x2+y2+4x-2y+4=0上的点的距离的最小值为 .
C
跟踪练习
4.已知直线l:mx+y-3=0与圆(x-1)2+(y-2)2=4交于A,B两点,过A,B分别做l的垂线与x轴交于C,D两点,若|AB|=4,则|CD|= .
解:圆(x-1)2+(y-2)2=4,圆心(1,2),半径r=2,
∵|AB|=4,∴直线l:mx+y-3=0过圆心(1,2),
∴m+2-3=0,∴m=1,
∴直线l:x+y-3=0,倾斜角为135°,
∵过A,B分别做l的垂线与x轴交于C,D两点,
课堂小结
本
课
结
束
