2.5.1 第2课时 直线与圆的方程的实际应用 课件(共21张PPT)
文档属性
| 名称 | 2.5.1 第2课时 直线与圆的方程的实际应用 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 675.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 17:11:19 | ||
图片预览







文档简介
(共21张PPT)
2.5.1 第2课时 直线与圆的方程的实际应用
第二章 直线和圆的方程
学习目标
学习目标
1.理解并掌握直线与圆的方程在实际生活中的应用.
2.会用“数形结合”的数学思想解决问题.
核心素养
1.能根据给定直线、圆的方程,判断直线与圆的位置关系.(逻辑推理)
2.能用直线和圆的方程解决一些简单的数学问题与实际问题.(数学建模)
直线与圆的方程的实际应用方法
仔细读题(审题)→建立数学模型→解答数学模型→检验,给出实际问题的答案.
新知探索
直线与圆的方程的实际应用方法
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,如点、直线,将平面几何问题转化为代数问题.
第二步:通过代数运算,解决代数问题.
第三步:把代数运算结果“翻译”成几何结论.
用坐标法解决平面几何问题的“三步曲”
新知探索
直线与圆的方程的实际应用方法
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,如点、直线,将平面几何问题转化为代数问题.
第二步:通过代数运算,解决代数问题.
第三步:把代数运算结果“翻译”成几何结论.
用坐标法解决平面几何问题的“三步曲”
新知探索
小试身手
1.一涵洞的横截面是半径为5 m的半圆,则该半圆的方程是( )
A.x2+y2=25
B.x2+y2=25(y≥0)
C.(x+5)2+y2=25(y≤0)
D.随建立直角坐标系的变化而变化
答案: D
典例精析
题型一:直线与圆的方程的应用
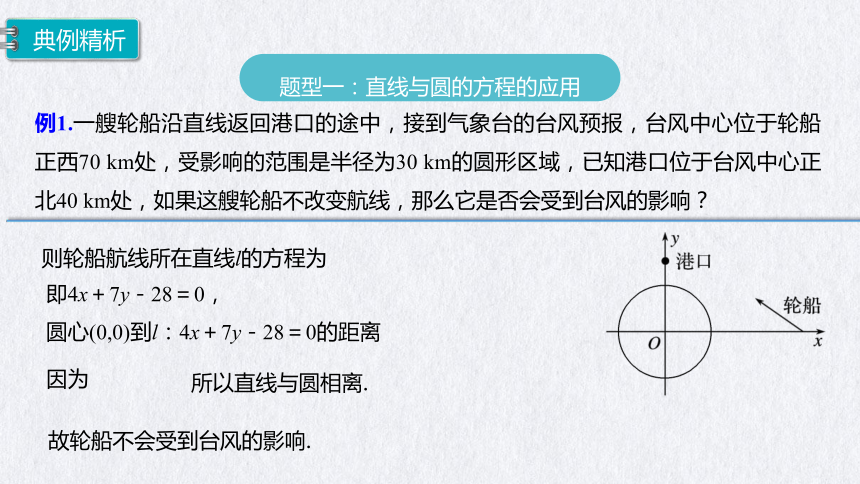
例1.一艘轮船沿直线返回港口的途中,接到气象台的台风预报,台风中心位于轮船正西70 km处,受影响的范围是半径为30 km的圆形区域,已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
解:以台风中心为坐标原点,以东西方向为x轴建立直角坐标系(如图所示),
其中取10 km为单位长度,
则受台风影响的圆形区域所对应的圆的方程为x2+y2=9,
港口所对应的点的坐标为(0,4),
轮船的初始位置所对应的点的坐标为(7,0),
典例精析
题型一:直线与圆的方程的应用
例1.一艘轮船沿直线返回港口的途中,接到气象台的台风预报,台风中心位于轮船正西70 km处,受影响的范围是半径为30 km的圆形区域,已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
则轮船航线所在直线l的方程为
即4x+7y-28=0,
圆心(0,0)到l:4x+7y-28=0的距离
因为
所以直线与圆相离.
故轮船不会受到台风的影响.
规律方法
题型一:直线与圆的方程的应用
解决直线与圆的实际应用题的步骤
(1)审题:从题目中抽象出几何模型,明确已知和未知.
(2)建系:建立适当的直角坐标系,用坐标和方程表示几何模型中的基本元素.
(3)求解:利用直线与圆的有关知识求出未知.
(4)还原:将运算结果还原到实际问题中去.
典例精析
题型二:坐标法的应用
例2.如图所示,AB是圆O的直径,CD是圆O的一条弦,且AB⊥CD,E为垂足.利用坐标法证明E是CD的中点.
证明:如图所示,以O为坐标原点,以直径AB所在直线为x轴建立平面直角坐标系,
设圆O的半径为r,|OE|=m,则圆O的方程为x2+y2=r2,
设C(m,b1),D(m,b2).
则
即b1,b2是关于b的方程m2+b2=r2的根,
解方程得
即(m,0).故E是CD的中点.
则CD的中点坐标为
不妨设
规律方法
题型二:坐标法
(1)坐标法建立直角坐标系应坚持的原则
①若有两条相互垂直的直线,一般以它们分别为x轴和y轴.
②充分利用图形的对称性.
③让尽可能多的点落在坐标轴上,或关于坐标轴对称.
④关键点的坐标易于求得.
(2)通过建立坐标系,将几何问题转化为代数问题,通过代数运算,求得结果.所以本例充分体现了数学建模和数学运算的数学核心素养.
典例精析
题型三:直线与圆的综合实际应用
例3.某圆拱桥的水面跨度是20 m,拱高为4 m.现有一船宽9 m,在水面以上部分高3 m,通行无阻.近日水位暴涨了1.5 m,为此,必须加重船载,降低船身,当船身至少降低____ m时,船才能安全通过桥洞.(结果精确到0.01 m)
解:以水位未涨前的水面AB的中点为原点,
建立平面直角坐标系,如图所示,
设圆拱所在圆的方程为x2+(y-b)2=r2,
∵圆经过点B(10,0),C(0,4),
解得:
典例精析
题型三:直线与圆的综合实际应用
例3.某圆拱桥的水面跨度是20 m,拱高为4 m.现有一船宽9 m,在水面以上部分高3 m,通行无阻.近日水位暴涨了1.5 m,为此,必须加重船载,降低船身,当船身至少降低____ m时,船才能安全通过桥洞.(结果精确到0.01 m)
∴圆的方程是x2+(y+10.5)2=14.52(0≤y≤4),令x=4.5,得y≈3.28,
故当水位暴涨1.5 m后,船身至少应降低1.5-(3.28-3)=1.22 (m),
船才能安全通过桥洞.
规律方法
实际应用的解题方法
在实际问题中,遇到有关直线和圆的问题,通常建立直角坐标系,利用坐标法解决.建立适当的直角坐标系应遵循三点:
(1)若曲线是轴对称图形,则可选它的对称轴为坐标轴;
(2)常选特殊点作为直角坐标系的原点;
(3)尽量使已知点位于坐标轴上.建立适当的直角坐标系,会简化运算过程.要想学会建立适当的直角坐标系,必须靠平时经验的积累.
跟踪练习
解析:从村庄外围到小路的最短距离为圆心(2,-3)到直线x-y+2=0的距离减去圆的半径2,
即
1.设某村庄外围成圆形,其所在曲线的方程可用(x-2)2+(y+3)2=4表示,村外一小路方程可用x-y+2=0表示,则从村庄外围到小路的最短距离是_________.
答案:-2
跟踪练习
2.如图,圆弧形拱桥的跨度AB=12 m,拱高CD=4 m,则拱桥的直径为________ m.
解析:设圆心为O,半径为r,则由勾股定理得,|OB|2=|OD|2+|BD|2,
所以拱桥的直径为13 m.
即
解得
答案:13
跟踪练习
3.一辆货车宽1.6米,要经过一个半径为3.6米的半圆形单行隧道,则这辆货车的平顶车篷的篷顶距离地面高度最高约为( )
A.2.4米 B.3.5米 C.3.6米 D.2.0米
解析:以半圆所在直径为x轴,过圆心且与x轴垂直的直线为y轴,建立如图所示的平面直角坐标系.
易知半圆所在的圆的方程为x2+y2=3.62(y≥0),
由图可知,当货车恰好在隧道中间行走时车篷最高,
此时x=0.8或x=-0.8,代入x2+y2=3.62,
得y≈3.5(负值舍去).
答案:B
所以选B.
跟踪练习
4.如图所示,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan ∠BCO= .
求新桥BC的长.
解:如图,以O为坐标原点,OC所在直线为x轴建立平面直角坐标系xOy.由条件知,A(0,60),C(170,0),
直线BC的斜率
跟踪练习
4.如图所示,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan ∠BCO= .
求新桥BC的长.
又因为AB⊥BC,所以直线AB的斜率
设点B的坐标为(a,b),
则
解得a=80,b=120.
因此新桥BC的长为150 m.
课堂小结
谢
指
导
谢
2.5.1 第2课时 直线与圆的方程的实际应用
第二章 直线和圆的方程
学习目标
学习目标
1.理解并掌握直线与圆的方程在实际生活中的应用.
2.会用“数形结合”的数学思想解决问题.
核心素养
1.能根据给定直线、圆的方程,判断直线与圆的位置关系.(逻辑推理)
2.能用直线和圆的方程解决一些简单的数学问题与实际问题.(数学建模)
直线与圆的方程的实际应用方法
仔细读题(审题)→建立数学模型→解答数学模型→检验,给出实际问题的答案.
新知探索
直线与圆的方程的实际应用方法
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,如点、直线,将平面几何问题转化为代数问题.
第二步:通过代数运算,解决代数问题.
第三步:把代数运算结果“翻译”成几何结论.
用坐标法解决平面几何问题的“三步曲”
新知探索
直线与圆的方程的实际应用方法
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,如点、直线,将平面几何问题转化为代数问题.
第二步:通过代数运算,解决代数问题.
第三步:把代数运算结果“翻译”成几何结论.
用坐标法解决平面几何问题的“三步曲”
新知探索
小试身手
1.一涵洞的横截面是半径为5 m的半圆,则该半圆的方程是( )
A.x2+y2=25
B.x2+y2=25(y≥0)
C.(x+5)2+y2=25(y≤0)
D.随建立直角坐标系的变化而变化
答案: D
典例精析
题型一:直线与圆的方程的应用
例1.一艘轮船沿直线返回港口的途中,接到气象台的台风预报,台风中心位于轮船正西70 km处,受影响的范围是半径为30 km的圆形区域,已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
解:以台风中心为坐标原点,以东西方向为x轴建立直角坐标系(如图所示),
其中取10 km为单位长度,
则受台风影响的圆形区域所对应的圆的方程为x2+y2=9,
港口所对应的点的坐标为(0,4),
轮船的初始位置所对应的点的坐标为(7,0),
典例精析
题型一:直线与圆的方程的应用
例1.一艘轮船沿直线返回港口的途中,接到气象台的台风预报,台风中心位于轮船正西70 km处,受影响的范围是半径为30 km的圆形区域,已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
则轮船航线所在直线l的方程为
即4x+7y-28=0,
圆心(0,0)到l:4x+7y-28=0的距离
因为
所以直线与圆相离.
故轮船不会受到台风的影响.
规律方法
题型一:直线与圆的方程的应用
解决直线与圆的实际应用题的步骤
(1)审题:从题目中抽象出几何模型,明确已知和未知.
(2)建系:建立适当的直角坐标系,用坐标和方程表示几何模型中的基本元素.
(3)求解:利用直线与圆的有关知识求出未知.
(4)还原:将运算结果还原到实际问题中去.
典例精析
题型二:坐标法的应用
例2.如图所示,AB是圆O的直径,CD是圆O的一条弦,且AB⊥CD,E为垂足.利用坐标法证明E是CD的中点.
证明:如图所示,以O为坐标原点,以直径AB所在直线为x轴建立平面直角坐标系,
设圆O的半径为r,|OE|=m,则圆O的方程为x2+y2=r2,
设C(m,b1),D(m,b2).
则
即b1,b2是关于b的方程m2+b2=r2的根,
解方程得
即(m,0).故E是CD的中点.
则CD的中点坐标为
不妨设
规律方法
题型二:坐标法
(1)坐标法建立直角坐标系应坚持的原则
①若有两条相互垂直的直线,一般以它们分别为x轴和y轴.
②充分利用图形的对称性.
③让尽可能多的点落在坐标轴上,或关于坐标轴对称.
④关键点的坐标易于求得.
(2)通过建立坐标系,将几何问题转化为代数问题,通过代数运算,求得结果.所以本例充分体现了数学建模和数学运算的数学核心素养.
典例精析
题型三:直线与圆的综合实际应用
例3.某圆拱桥的水面跨度是20 m,拱高为4 m.现有一船宽9 m,在水面以上部分高3 m,通行无阻.近日水位暴涨了1.5 m,为此,必须加重船载,降低船身,当船身至少降低____ m时,船才能安全通过桥洞.(结果精确到0.01 m)
解:以水位未涨前的水面AB的中点为原点,
建立平面直角坐标系,如图所示,
设圆拱所在圆的方程为x2+(y-b)2=r2,
∵圆经过点B(10,0),C(0,4),
解得:
典例精析
题型三:直线与圆的综合实际应用
例3.某圆拱桥的水面跨度是20 m,拱高为4 m.现有一船宽9 m,在水面以上部分高3 m,通行无阻.近日水位暴涨了1.5 m,为此,必须加重船载,降低船身,当船身至少降低____ m时,船才能安全通过桥洞.(结果精确到0.01 m)
∴圆的方程是x2+(y+10.5)2=14.52(0≤y≤4),令x=4.5,得y≈3.28,
故当水位暴涨1.5 m后,船身至少应降低1.5-(3.28-3)=1.22 (m),
船才能安全通过桥洞.
规律方法
实际应用的解题方法
在实际问题中,遇到有关直线和圆的问题,通常建立直角坐标系,利用坐标法解决.建立适当的直角坐标系应遵循三点:
(1)若曲线是轴对称图形,则可选它的对称轴为坐标轴;
(2)常选特殊点作为直角坐标系的原点;
(3)尽量使已知点位于坐标轴上.建立适当的直角坐标系,会简化运算过程.要想学会建立适当的直角坐标系,必须靠平时经验的积累.
跟踪练习
解析:从村庄外围到小路的最短距离为圆心(2,-3)到直线x-y+2=0的距离减去圆的半径2,
即
1.设某村庄外围成圆形,其所在曲线的方程可用(x-2)2+(y+3)2=4表示,村外一小路方程可用x-y+2=0表示,则从村庄外围到小路的最短距离是_________.
答案:-2
跟踪练习
2.如图,圆弧形拱桥的跨度AB=12 m,拱高CD=4 m,则拱桥的直径为________ m.
解析:设圆心为O,半径为r,则由勾股定理得,|OB|2=|OD|2+|BD|2,
所以拱桥的直径为13 m.
即
解得
答案:13
跟踪练习
3.一辆货车宽1.6米,要经过一个半径为3.6米的半圆形单行隧道,则这辆货车的平顶车篷的篷顶距离地面高度最高约为( )
A.2.4米 B.3.5米 C.3.6米 D.2.0米
解析:以半圆所在直径为x轴,过圆心且与x轴垂直的直线为y轴,建立如图所示的平面直角坐标系.
易知半圆所在的圆的方程为x2+y2=3.62(y≥0),
由图可知,当货车恰好在隧道中间行走时车篷最高,
此时x=0.8或x=-0.8,代入x2+y2=3.62,
得y≈3.5(负值舍去).
答案:B
所以选B.
跟踪练习
4.如图所示,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan ∠BCO= .
求新桥BC的长.
解:如图,以O为坐标原点,OC所在直线为x轴建立平面直角坐标系xOy.由条件知,A(0,60),C(170,0),
直线BC的斜率
跟踪练习
4.如图所示,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan ∠BCO= .
求新桥BC的长.
又因为AB⊥BC,所以直线AB的斜率
设点B的坐标为(a,b),
则
解得a=80,b=120.
因此新桥BC的长为150 m.
课堂小结
谢
指
导
谢
