2.5.2圆与圆的位置关系 课件(共25张PPT)
文档属性
| 名称 | 2.5.2圆与圆的位置关系 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 567.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 17:11:40 | ||
图片预览


文档简介
(共25张PPT)
2.5.2 圆与圆的位置关系
第二章 直线和圆的方程
学习目标
学习目标
1.掌握圆与圆的位置关系及判定方法.(重点)
2.了解两圆相离、相交或相切时一些简单的几何性质的应用.(重点)
3.掌握利用圆的对称性灵活解决问题的方法.(难点)
核心素养
1.通过学习圆与圆的位置关系,培养直观想象的核心素养.
2.借助圆与圆的位置关系的判断,培养数学运算的核心素养.
问题引入
圆与圆的位置关系
魔术钢圈有很多的版本,通常有三连环和四连环.三连环中,有一个环是有缺口的,而另外两个环是密封的;而四连环的原理基本相同,唯一不同的是有两个环本来就连在一起,其余是一个有缺口的环和一个密封的环.表演时基本的手法是敲击法和摩擦法.敲击法:一手拿一个环,右手拿的是有缺口的环.缺口环的口要在右手的尾指处.用右手的环敲击左手的环.先装作敲两下,第三下时右手的环迅速向下敲,同时让左手的环的上端穿过右手的环的缺口,穿进去后便连在一起.摩擦法:同样一手拿一个环,其中一个当然是缺口环,不过你哪一只手拿缺口环都行.把两个环靠在一起,让两个环的一端进行摩擦.当然,缺口不能让别人看到,要用食指捂住.当两个环摩擦时,趁机让普通环的一端直接滑入缺口环的缺口处.成功滑入后,再摩擦两下,拉直两个环就行啦.
新知探索
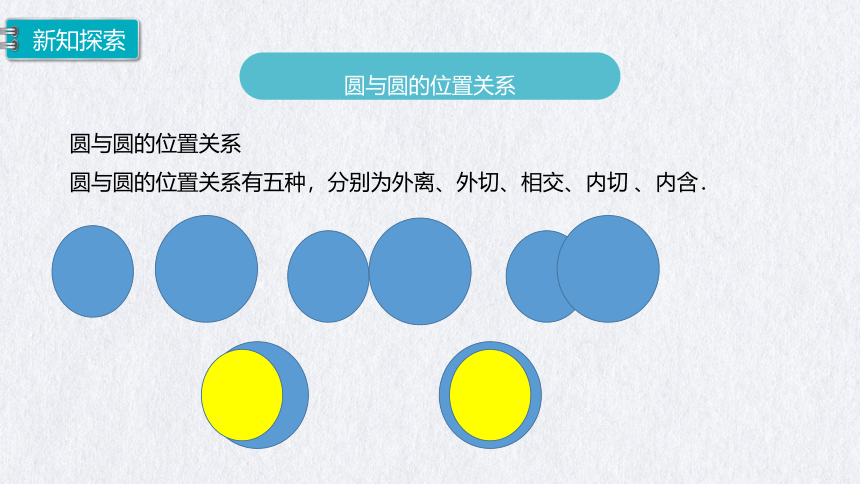
圆与圆的位置关系
圆与圆的位置关系
圆与圆的位置关系有五种,分别为外离、外切、相交、内切 、内含.
O
新知探索
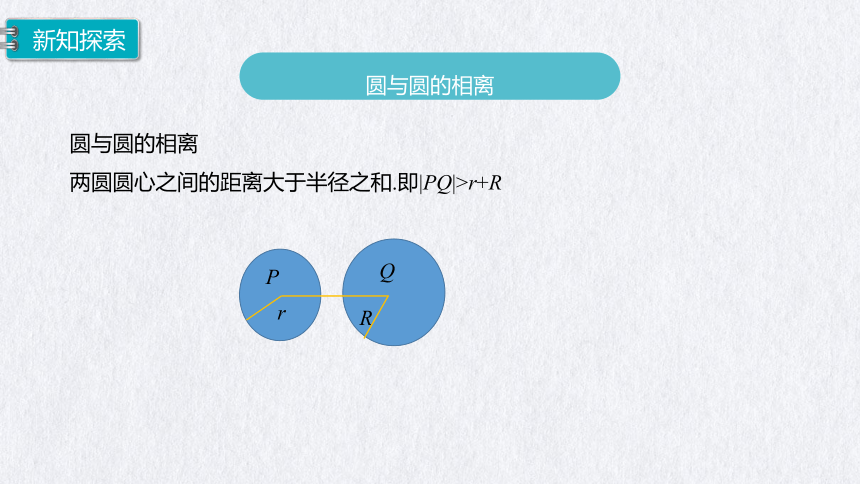
圆与圆的相离
圆与圆的相离
两圆圆心之间的距离大于半径之和.即|PQ|>r+R
O
P
Q
R
r
新知探索
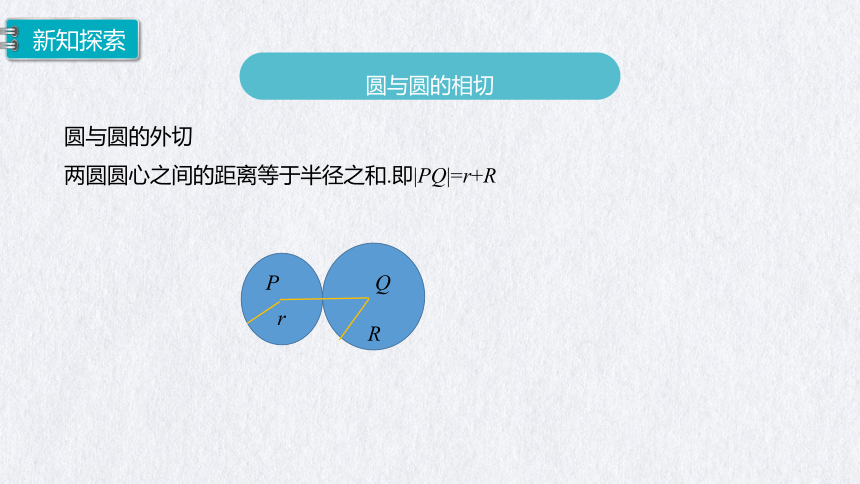
圆与圆的相切
圆与圆的外切
两圆圆心之间的距离等于半径之和.即|PQ|=r+R
P
Q
R
r
新知探索
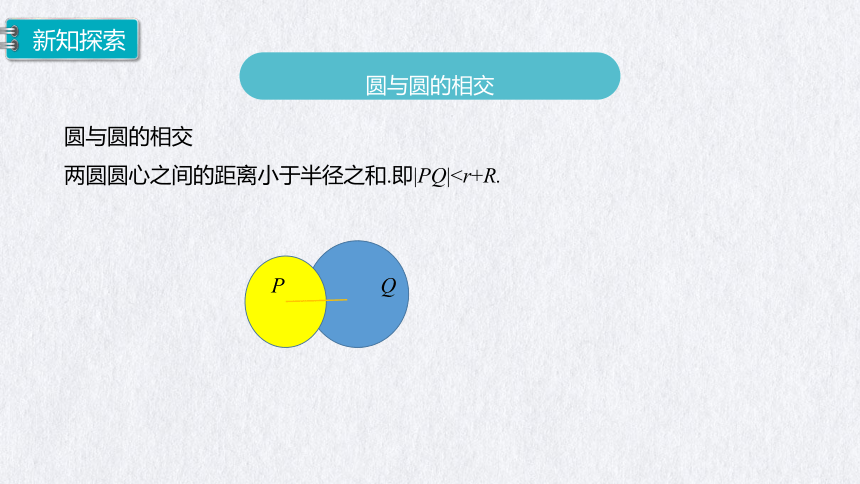
圆与圆的相交
圆与圆的相交
两圆圆心之间的距离小于半径之和.即|PQ|P
Q
新知探索
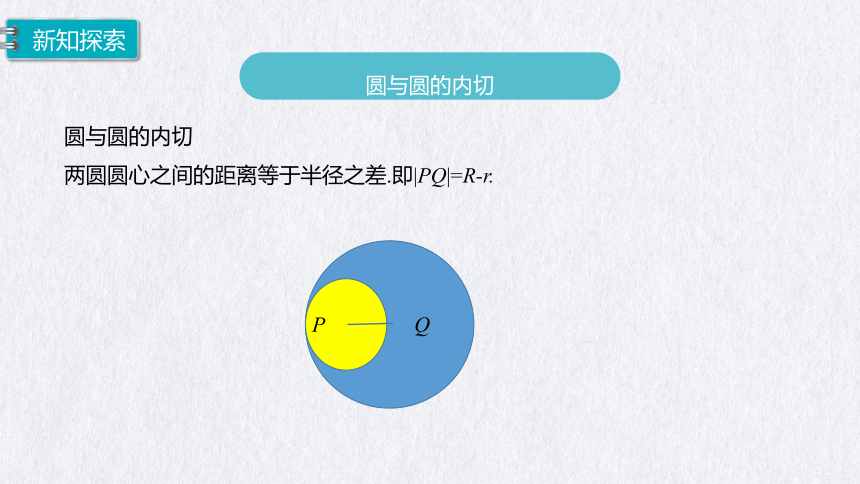
圆与圆的内切
圆与圆的内切
两圆圆心之间的距离等于半径之差.即|PQ|=R-r.
P
Q
新知探索
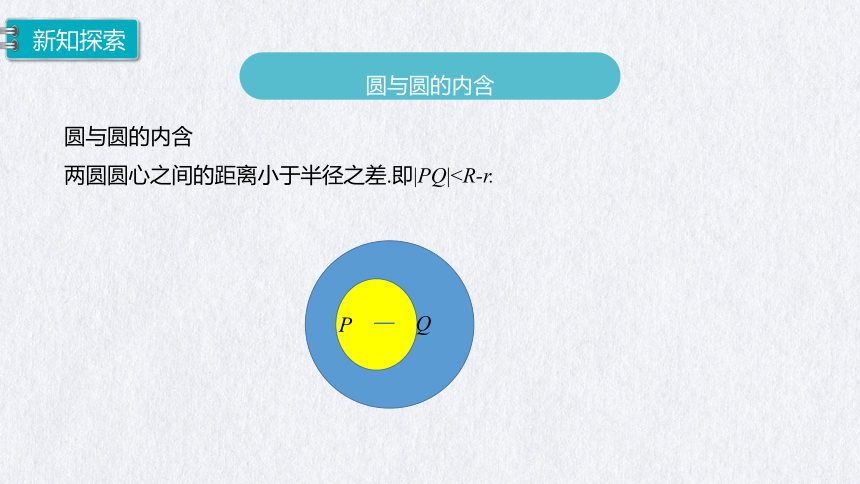
圆与圆的内含
圆与圆的内含
两圆圆心之间的距离小于半径之差.即|PQ|P
Q
新知探索
圆与圆的位置关系
圆与圆的位置关系
圆与圆的位置关系有五种,分别为外离、外切、相交、内切 、内含.
O
新知探索
代数法判断圆与圆的位置关系
代数法:设两圆的一般方程为
联立方程
则方程组解的个数与两圆的位置关系如下:
方程组解的个数 2 1 0
两圆的公共点的个数 2 1 0
两圆的位置关系 相交 外切或内切 外离或内含
新知探索
圆与圆的位置关系
微判断
如果两个圆的方程组成的方程组只有一组实数解,则两圆外切. ( )
答案:×
微思考
如果两圆相交,如何得到这两圆的公共弦所在的直线方程
提示:当两圆相交时,可解两圆的方程所组成的方程组,得到两交点坐标,利用两点式得到两圆的公共弦所在的直线方程,也可以把两圆的方程作差消去x2和y2,就得到两圆的公共弦所在的直线方程.
典例精析
题型一:两圆的位置关系判断
例1.(1)圆O1:x2+y2-2x=0与圆O2:x2+y2-2y=0的位置关系是( )
A.外离 B.相交 C.外切 D.内切
(2)圆O1:(x+2)2+(y-2)2=1与圆O2:(x-2)2+(y-5)2=16的位置关系为 .
所以两圆相外切.
解:(1)两圆的标准方程为(x-1)2+y2=1和x2+(y-1)2=1,对应圆心坐标为O1(1,0),半径为1,和圆心坐标O2(0,1),半径为1,则圆心距离|O1O2|=
则0<|O1O2|<2,即两圆相交,故选B.
(2)两圆的圆心分别为O1(-2,2),O2(2,5),半径分别为r1=1,r2=4,所以
规律方法
判断两圆的位置关系常用两种方法
几何法和代数法,但一般情况下用几何法,即用两圆半径和圆心距之间的关系来刻画,此种方法形象直观,关键是明确圆心和半径,再套用圆与圆位置关系的关系式进行求解或判断.
题型一:两圆的位置关系的判断
典例精析
题型二:两圆的公共弦
例2.已知两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0.
(1)判断两圆是否相交,若相交,求出公共弦所在的直线方程,若不相交,请说明理由;
(2)求公共弦的长度.
解:(1)相交.
将两圆方程配方化为标准方程,则
C1:(x-1)2+(y+5)2=50,
C2:(x+1)2+(y+1)2=10,
∴圆C1的圆心坐标为(1,-5),半径为r1=
,
圆C2的圆心坐标为(-1,-1),半径为r2=
∴|r1-r2|<|C1C2|∴两圆相交.
将两圆方程相减,得公共弦所在的直线方程为x-2y+4=0.
典例精析
题型二:两圆的公共弦
例2.已知两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0.
(1)判断两圆是否相交,若相交,求出公共弦所在的直线方程,若不相交,请说明理由;
(2)求公共弦的长度.
,
方法二:设两圆相交于点A,B,则A,B两点满足方程组
∴公共弦长为
解:(2)方法一:由(1)知圆C1的圆心(1,-5)到直线x-2y+4=0的距离为
解得 或
所以,公共弦长为
规律方法
1.当两圆相交时,公共弦所在的直线方程的求法
若圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0相交,则两圆公共弦所在的直线方程为(D1-D2)x+(E1-E2)y+F1-F2=0.
2.公共弦长的求法
(1)代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.
(2)几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.
公共弦长和公共直线
典例精析
题型三:圆系方程
解:(1)∵曲线(1+λ)x2+(1+λ)y2+(6-4λ)x-16-6λ=0可化为(x2+y2+6x-16)+λ(x2+y2-4x-6)=0,
∴x2+y2+6x-16=0且x2+y2-4x-6=0,
可得恒过定点(1,3)和(1,-3).
答案:(1,3)和(1,-3)
例3 .(1)对于任意实数λ,曲线(1+λ)x2+(1+λ)y2+(6-4λ)x-16-6λ=0恒过定点 .
(2)求过直线x+y+4=0与圆x2+y2+4x-2y-4=0的交点且与直线y=x相切的圆的方程.
(2)设所求圆的方程为
x2+y2+4x-2y-4+λ(x+y+4)=0.
联立
得x2+(1+λ)x+2(λ-1)=0.因为所求圆与直线y=x相切,所以Δ=0,即(1+λ)2-8(λ-1)=0,解得λ=3,
故所求圆的方程为x2+y2+7x+y+8=0.
规律方法
题型三:圆系方程
在求解过直线与直线交点、直线与圆交点、圆与圆的交点的圆有关问题时,若能巧妙使用直线系与圆系方程,往往能优化解题过程,减少运算量,收到事半功倍的效果.
跟踪练习
1.圆(x-3)2+(y+2)2=1与圆x2+y2-14x-2y+14=0的位置关系是( )
A.外切 B.内切 C.相交 D.外离
答案:B
解:圆x2+y2-14x-2y+14=0变形为(x-7)2+(y-1)2=36,
圆心坐标为(7,1),半径为r1=6,
圆(x-3)2+(y+2)2=1的圆心坐标为(3,-2),半径为
所以圆心距
所以两圆内切
跟踪练习
2.圆x2+y2-4x+6y=0和圆x2+y2-6x=0交于A,B两点,则AB的垂直平分线的方程是( )
A.x+y+3=0 B.2x-y-5=0 C.3x-y-9=0 D.4x-3y+7=0
解:AB的垂直平分线过两圆的圆心,把圆心(2,-3)代入,即可排除A,B,D.
答案:C
跟踪练习
3.若圆C1:(x+2)2+(y-m)2=9与圆C2:(x-m)2+(y+1)2=4外切,则m的值为 .
解:两圆的圆心坐标分别为(-2,m),(m,-1),
两圆的半径分别为3,2,
又因为
所以 ,m=2或-5.
跟踪练习
4.圆C1:x2+y2-2x-8=0与圆C2:x2+y2+2x-4y-4=0的公共弦长为 .
解析:由圆C1与圆C2的公共弦所在的直线l的方程为x-y+1=0,得点C1(1,0)到直线l的距离为
因为,圆C1的半径为r1=3,所以圆C1与圆C2的公共弦长为
课堂小结
本
课
结
束
2.5.2 圆与圆的位置关系
第二章 直线和圆的方程
学习目标
学习目标
1.掌握圆与圆的位置关系及判定方法.(重点)
2.了解两圆相离、相交或相切时一些简单的几何性质的应用.(重点)
3.掌握利用圆的对称性灵活解决问题的方法.(难点)
核心素养
1.通过学习圆与圆的位置关系,培养直观想象的核心素养.
2.借助圆与圆的位置关系的判断,培养数学运算的核心素养.
问题引入
圆与圆的位置关系
魔术钢圈有很多的版本,通常有三连环和四连环.三连环中,有一个环是有缺口的,而另外两个环是密封的;而四连环的原理基本相同,唯一不同的是有两个环本来就连在一起,其余是一个有缺口的环和一个密封的环.表演时基本的手法是敲击法和摩擦法.敲击法:一手拿一个环,右手拿的是有缺口的环.缺口环的口要在右手的尾指处.用右手的环敲击左手的环.先装作敲两下,第三下时右手的环迅速向下敲,同时让左手的环的上端穿过右手的环的缺口,穿进去后便连在一起.摩擦法:同样一手拿一个环,其中一个当然是缺口环,不过你哪一只手拿缺口环都行.把两个环靠在一起,让两个环的一端进行摩擦.当然,缺口不能让别人看到,要用食指捂住.当两个环摩擦时,趁机让普通环的一端直接滑入缺口环的缺口处.成功滑入后,再摩擦两下,拉直两个环就行啦.
新知探索
圆与圆的位置关系
圆与圆的位置关系
圆与圆的位置关系有五种,分别为外离、外切、相交、内切 、内含.
O
新知探索
圆与圆的相离
圆与圆的相离
两圆圆心之间的距离大于半径之和.即|PQ|>r+R
O
P
Q
R
r
新知探索
圆与圆的相切
圆与圆的外切
两圆圆心之间的距离等于半径之和.即|PQ|=r+R
P
Q
R
r
新知探索
圆与圆的相交
圆与圆的相交
两圆圆心之间的距离小于半径之和.即|PQ|
Q
新知探索
圆与圆的内切
圆与圆的内切
两圆圆心之间的距离等于半径之差.即|PQ|=R-r.
P
Q
新知探索
圆与圆的内含
圆与圆的内含
两圆圆心之间的距离小于半径之差.即|PQ|
Q
新知探索
圆与圆的位置关系
圆与圆的位置关系
圆与圆的位置关系有五种,分别为外离、外切、相交、内切 、内含.
O
新知探索
代数法判断圆与圆的位置关系
代数法:设两圆的一般方程为
联立方程
则方程组解的个数与两圆的位置关系如下:
方程组解的个数 2 1 0
两圆的公共点的个数 2 1 0
两圆的位置关系 相交 外切或内切 外离或内含
新知探索
圆与圆的位置关系
微判断
如果两个圆的方程组成的方程组只有一组实数解,则两圆外切. ( )
答案:×
微思考
如果两圆相交,如何得到这两圆的公共弦所在的直线方程
提示:当两圆相交时,可解两圆的方程所组成的方程组,得到两交点坐标,利用两点式得到两圆的公共弦所在的直线方程,也可以把两圆的方程作差消去x2和y2,就得到两圆的公共弦所在的直线方程.
典例精析
题型一:两圆的位置关系判断
例1.(1)圆O1:x2+y2-2x=0与圆O2:x2+y2-2y=0的位置关系是( )
A.外离 B.相交 C.外切 D.内切
(2)圆O1:(x+2)2+(y-2)2=1与圆O2:(x-2)2+(y-5)2=16的位置关系为 .
所以两圆相外切.
解:(1)两圆的标准方程为(x-1)2+y2=1和x2+(y-1)2=1,对应圆心坐标为O1(1,0),半径为1,和圆心坐标O2(0,1),半径为1,则圆心距离|O1O2|=
则0<|O1O2|<2,即两圆相交,故选B.
(2)两圆的圆心分别为O1(-2,2),O2(2,5),半径分别为r1=1,r2=4,所以
规律方法
判断两圆的位置关系常用两种方法
几何法和代数法,但一般情况下用几何法,即用两圆半径和圆心距之间的关系来刻画,此种方法形象直观,关键是明确圆心和半径,再套用圆与圆位置关系的关系式进行求解或判断.
题型一:两圆的位置关系的判断
典例精析
题型二:两圆的公共弦
例2.已知两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0.
(1)判断两圆是否相交,若相交,求出公共弦所在的直线方程,若不相交,请说明理由;
(2)求公共弦的长度.
解:(1)相交.
将两圆方程配方化为标准方程,则
C1:(x-1)2+(y+5)2=50,
C2:(x+1)2+(y+1)2=10,
∴圆C1的圆心坐标为(1,-5),半径为r1=
,
圆C2的圆心坐标为(-1,-1),半径为r2=
∴|r1-r2|<|C1C2|
将两圆方程相减,得公共弦所在的直线方程为x-2y+4=0.
典例精析
题型二:两圆的公共弦
例2.已知两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0.
(1)判断两圆是否相交,若相交,求出公共弦所在的直线方程,若不相交,请说明理由;
(2)求公共弦的长度.
,
方法二:设两圆相交于点A,B,则A,B两点满足方程组
∴公共弦长为
解:(2)方法一:由(1)知圆C1的圆心(1,-5)到直线x-2y+4=0的距离为
解得 或
所以,公共弦长为
规律方法
1.当两圆相交时,公共弦所在的直线方程的求法
若圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0相交,则两圆公共弦所在的直线方程为(D1-D2)x+(E1-E2)y+F1-F2=0.
2.公共弦长的求法
(1)代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.
(2)几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.
公共弦长和公共直线
典例精析
题型三:圆系方程
解:(1)∵曲线(1+λ)x2+(1+λ)y2+(6-4λ)x-16-6λ=0可化为(x2+y2+6x-16)+λ(x2+y2-4x-6)=0,
∴x2+y2+6x-16=0且x2+y2-4x-6=0,
可得恒过定点(1,3)和(1,-3).
答案:(1,3)和(1,-3)
例3 .(1)对于任意实数λ,曲线(1+λ)x2+(1+λ)y2+(6-4λ)x-16-6λ=0恒过定点 .
(2)求过直线x+y+4=0与圆x2+y2+4x-2y-4=0的交点且与直线y=x相切的圆的方程.
(2)设所求圆的方程为
x2+y2+4x-2y-4+λ(x+y+4)=0.
联立
得x2+(1+λ)x+2(λ-1)=0.因为所求圆与直线y=x相切,所以Δ=0,即(1+λ)2-8(λ-1)=0,解得λ=3,
故所求圆的方程为x2+y2+7x+y+8=0.
规律方法
题型三:圆系方程
在求解过直线与直线交点、直线与圆交点、圆与圆的交点的圆有关问题时,若能巧妙使用直线系与圆系方程,往往能优化解题过程,减少运算量,收到事半功倍的效果.
跟踪练习
1.圆(x-3)2+(y+2)2=1与圆x2+y2-14x-2y+14=0的位置关系是( )
A.外切 B.内切 C.相交 D.外离
答案:B
解:圆x2+y2-14x-2y+14=0变形为(x-7)2+(y-1)2=36,
圆心坐标为(7,1),半径为r1=6,
圆(x-3)2+(y+2)2=1的圆心坐标为(3,-2),半径为
所以圆心距
所以两圆内切
跟踪练习
2.圆x2+y2-4x+6y=0和圆x2+y2-6x=0交于A,B两点,则AB的垂直平分线的方程是( )
A.x+y+3=0 B.2x-y-5=0 C.3x-y-9=0 D.4x-3y+7=0
解:AB的垂直平分线过两圆的圆心,把圆心(2,-3)代入,即可排除A,B,D.
答案:C
跟踪练习
3.若圆C1:(x+2)2+(y-m)2=9与圆C2:(x-m)2+(y+1)2=4外切,则m的值为 .
解:两圆的圆心坐标分别为(-2,m),(m,-1),
两圆的半径分别为3,2,
又因为
所以 ,m=2或-5.
跟踪练习
4.圆C1:x2+y2-2x-8=0与圆C2:x2+y2+2x-4y-4=0的公共弦长为 .
解析:由圆C1与圆C2的公共弦所在的直线l的方程为x-y+1=0,得点C1(1,0)到直线l的距离为
因为,圆C1的半径为r1=3,所以圆C1与圆C2的公共弦长为
课堂小结
本
课
结
束
