广东省汕头市育能实高2022-2023学年高二下学期期中考试数学试题(含答案)
文档属性
| 名称 | 广东省汕头市育能实高2022-2023学年高二下学期期中考试数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 887.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 18:59:06 | ||
图片预览




文档简介
班级: 姓名: 座号:
一、单选题
1.已知全集,集合,则( UA)∩B=( )
A. B. C. D.
2.复数满足方程,则( )
A.2 B. C. D.8
3.在正项等比数列中,若,则( )
A.6 B.12 C.56 D.78
4.设,,,则a,b,c的大小关系是( )
A. B. C. D.
5.已知向量,,若,则( )
A. B. C. D.
6.意大利画家列奥纳多·达·芬奇的画作《抱银鼠的女子》(如图所示)中,女士颈部的黑色珍珠项链与她怀中的白貂形成对比.光线和阴影衬托出人物的优雅和柔美.达·芬奇提出:固定项链的两端,使其在重力的作用下自然下垂,形成的曲线是什么?这就是著名的“悬链线问题”.后人研究得出,悬链线并不是抛物线,而是与解析式为的“双曲余弦函数”相关.下列选项为“双曲余弦函数”图象的是( )
A.B.C.D.
7.在中,为上一点,为线段上任一点(不含端点),若,则的最小值是( )
A.8 B.10 C.13 D.16
8.已知椭圆的上焦点为,过原点的直线交于点,且,若,则的离心率为( )
A. B. C. D.
二、多选题
9.下列求导正确的是( )
A. B. C. D.
10.已知数列满足,,则( )
A.为等比数列 B.的通项公式为
C.为递增数列 D.的前n项和
11.函数的图象如图所示,则( )
A. B.的单调递减区间为
C.对任意的都有
D.在区间上的零点之和为
12.如图所示,在棱长为2的正方形中,点,分别是,的中点,则( )
A. B.与平面所成角的正弦值为
C.二面角的余弦值为
D.平面截正方体所得的截面周长为
三、填空题
13.(x﹣)4的展开式中的常数项为_____.
14.在2022年北京冬奥会志愿者选拔期间,来自北京某大学的4名男生和2名女生通过了志愿者的选拔.从这6名志愿者中挑选3名负责滑雪项目的服务工作,要求至少有一名女生,则不同的选法共有___________种.(请用数字作答)
15.直线:被圆:截得的弦长为_____________.
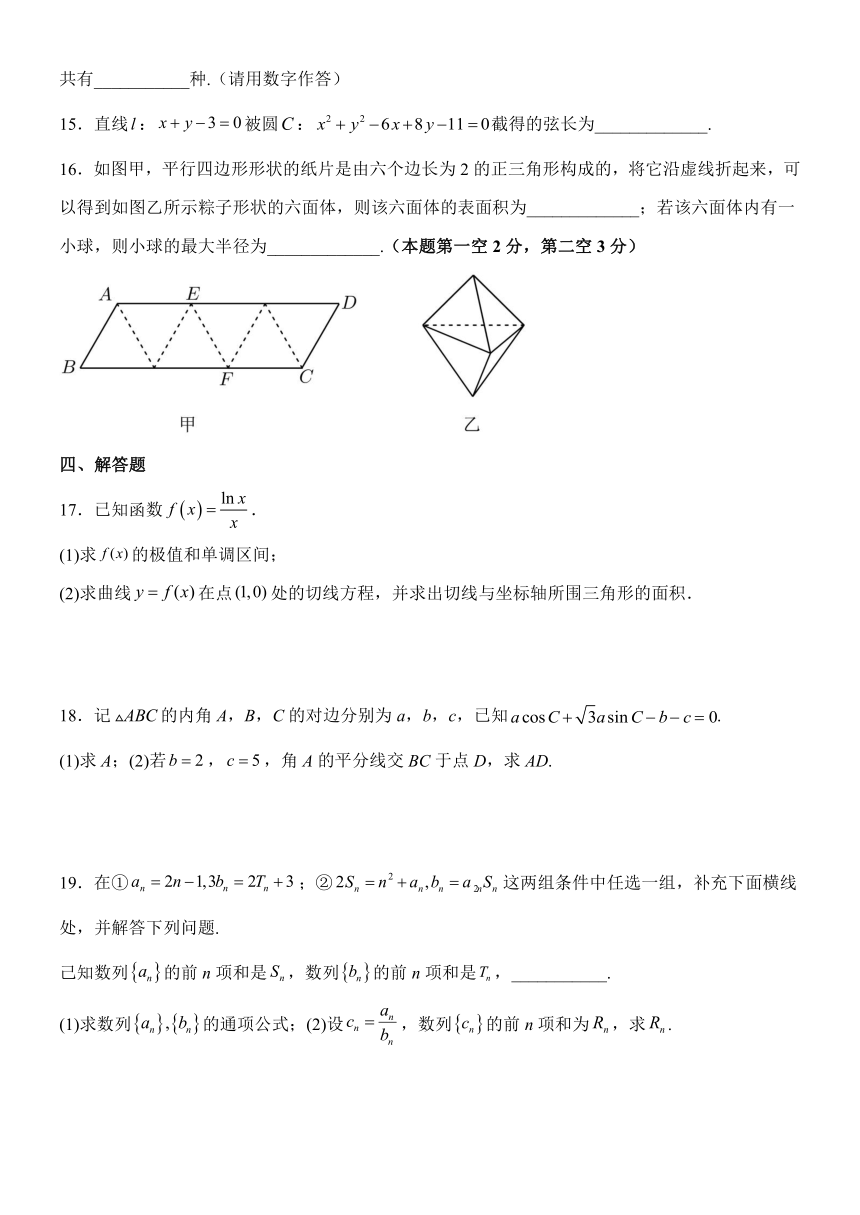
16.如图甲,平行四边形形状的纸片是由六个边长为2的正三角形构成的,将它沿虚线折起来,可以得到如图乙所示粽子形状的六面体,则该六面体的表面积为_____________;若该六面体内有一小球,则小球的最大半径为_____________.(本题第一空2分,第二空3分)
四、解答题
17.已知函数.
(1)求的极值和单调区间;
(2)求曲线在点处的切线方程,并求出切线与坐标轴所围三角形的面积.
18.记的内角A,B,C的对边分别为a,b,c,已知.
(1)求A;(2)若,,角A的平分线交BC于点D,求AD.
19.在①;②这两组条件中任选一组,补充下面横线处,并解答下列问题.
己知数列的前n项和是,数列的前n项和是,___________.
(1)求数列的通项公式;(2)设,数列的前n项和为,求.
20.如图,在四棱锥中,底面是矩形,侧棱底面,点为棱的中点,,.
(1)求证:∥平面;
(2)求平面与平面夹角的余弦值.
21.已知离心率为的椭圆,其焦距为.
(1)求此椭圆的方程;
(2)已知直线与椭圆交于两点,若以线段为直径的圆过点,求的值.
22.已知函数.
(1)若是的极值点,求的值;
(2)讨论函数的单调性;
(3)若恒成立,求a的取值范围;
参考答案:
1-8: DBDBBCDA
9.BCD 10.AD 11.AB 12.BD
13. 6 14. 16 15. 16. ;.
17.【详解】(1),
当时,,当时,,
所以函数的单调减区间为,单调增区间为,
所以,无极小值;
(2)由(1)得,,则所求切线的斜率为1,
故所求切线方程为,
当时,,当时,,
故切线与坐标轴所围三角形的面积.
【详解】(1)由已知及正弦定理得
,
因为,则,
所以,即.
又,所以,即,
因为,所以,
所以,得.
(2)因为是角的角平分线,
所以,
即,
结合(1)得,
解得.
19.【详解】(1)选条件①:由,可得,
两式相减可得,所以,
在中,令,可得,所以,
所以是以为首项,公比为的等比数列,,
故数列的通项公式为,数列的通项公式为;
选条件②:由,可得,
两式相减可得,即,
所以,
在中,令,可得,所以,
所以由,,,,
所以,从而有,
所以,,
故数列的通项公式为,数列的通项公式为;
(2)选条件①:由(1)知,
,
,
,
两式相减可得
,
所以,即;
选条件②:由(1)知,
所以.
20.【详解】(1)因为底面是矩形,所以.
因为平面,所以,.
以为原点,,,所在直线分别为轴、轴,轴,建立如图所示的空间直角坐标系,
则,0,,,0,,,2,,,2,,,0,,,1,,
所以.
设平面的一个法向量为,
则,即
取,则,.
所以 是平面的一个法向量.
因为,则,又平面,
所以平面.
(2)由(1)可知,,
又因为,平面,所以平面.
所以 是平面的一个法向量.
设平面与平面的夹角为,
则,
所以平面与平面夹角的余弦值为.
【详解】(1)解:由题知 解得 ,
椭圆的方程为.
(2)将代入椭圆方程,得,
又直线与椭圆有两个交点,,解得.
设,则.
若以为直径的圆过点,则.
又,
.
而,
,
,
,
解得,满足,故.
22.【详解】(1)因为
则,即,所以,经检验符合题意
(2).
当时,,所以在上单调递增;
当时,令,解得,
当时,;
当时,;
所以在上单调递增,在上单调递减;
(3)的定义域为,若恒成立,则恒成立,
即恒成立,
令,只需,又,
令得,
时,,则单调递增;
时,,则单调递减;
所以,解得:;
一、单选题
1.已知全集,集合,则( UA)∩B=( )
A. B. C. D.
2.复数满足方程,则( )
A.2 B. C. D.8
3.在正项等比数列中,若,则( )
A.6 B.12 C.56 D.78
4.设,,,则a,b,c的大小关系是( )
A. B. C. D.
5.已知向量,,若,则( )
A. B. C. D.
6.意大利画家列奥纳多·达·芬奇的画作《抱银鼠的女子》(如图所示)中,女士颈部的黑色珍珠项链与她怀中的白貂形成对比.光线和阴影衬托出人物的优雅和柔美.达·芬奇提出:固定项链的两端,使其在重力的作用下自然下垂,形成的曲线是什么?这就是著名的“悬链线问题”.后人研究得出,悬链线并不是抛物线,而是与解析式为的“双曲余弦函数”相关.下列选项为“双曲余弦函数”图象的是( )
A.B.C.D.
7.在中,为上一点,为线段上任一点(不含端点),若,则的最小值是( )
A.8 B.10 C.13 D.16
8.已知椭圆的上焦点为,过原点的直线交于点,且,若,则的离心率为( )
A. B. C. D.
二、多选题
9.下列求导正确的是( )
A. B. C. D.
10.已知数列满足,,则( )
A.为等比数列 B.的通项公式为
C.为递增数列 D.的前n项和
11.函数的图象如图所示,则( )
A. B.的单调递减区间为
C.对任意的都有
D.在区间上的零点之和为
12.如图所示,在棱长为2的正方形中,点,分别是,的中点,则( )
A. B.与平面所成角的正弦值为
C.二面角的余弦值为
D.平面截正方体所得的截面周长为
三、填空题
13.(x﹣)4的展开式中的常数项为_____.
14.在2022年北京冬奥会志愿者选拔期间,来自北京某大学的4名男生和2名女生通过了志愿者的选拔.从这6名志愿者中挑选3名负责滑雪项目的服务工作,要求至少有一名女生,则不同的选法共有___________种.(请用数字作答)
15.直线:被圆:截得的弦长为_____________.
16.如图甲,平行四边形形状的纸片是由六个边长为2的正三角形构成的,将它沿虚线折起来,可以得到如图乙所示粽子形状的六面体,则该六面体的表面积为_____________;若该六面体内有一小球,则小球的最大半径为_____________.(本题第一空2分,第二空3分)
四、解答题
17.已知函数.
(1)求的极值和单调区间;
(2)求曲线在点处的切线方程,并求出切线与坐标轴所围三角形的面积.
18.记的内角A,B,C的对边分别为a,b,c,已知.
(1)求A;(2)若,,角A的平分线交BC于点D,求AD.
19.在①;②这两组条件中任选一组,补充下面横线处,并解答下列问题.
己知数列的前n项和是,数列的前n项和是,___________.
(1)求数列的通项公式;(2)设,数列的前n项和为,求.
20.如图,在四棱锥中,底面是矩形,侧棱底面,点为棱的中点,,.
(1)求证:∥平面;
(2)求平面与平面夹角的余弦值.
21.已知离心率为的椭圆,其焦距为.
(1)求此椭圆的方程;
(2)已知直线与椭圆交于两点,若以线段为直径的圆过点,求的值.
22.已知函数.
(1)若是的极值点,求的值;
(2)讨论函数的单调性;
(3)若恒成立,求a的取值范围;
参考答案:
1-8: DBDBBCDA
9.BCD 10.AD 11.AB 12.BD
13. 6 14. 16 15. 16. ;.
17.【详解】(1),
当时,,当时,,
所以函数的单调减区间为,单调增区间为,
所以,无极小值;
(2)由(1)得,,则所求切线的斜率为1,
故所求切线方程为,
当时,,当时,,
故切线与坐标轴所围三角形的面积.
【详解】(1)由已知及正弦定理得
,
因为,则,
所以,即.
又,所以,即,
因为,所以,
所以,得.
(2)因为是角的角平分线,
所以,
即,
结合(1)得,
解得.
19.【详解】(1)选条件①:由,可得,
两式相减可得,所以,
在中,令,可得,所以,
所以是以为首项,公比为的等比数列,,
故数列的通项公式为,数列的通项公式为;
选条件②:由,可得,
两式相减可得,即,
所以,
在中,令,可得,所以,
所以由,,,,
所以,从而有,
所以,,
故数列的通项公式为,数列的通项公式为;
(2)选条件①:由(1)知,
,
,
,
两式相减可得
,
所以,即;
选条件②:由(1)知,
所以.
20.【详解】(1)因为底面是矩形,所以.
因为平面,所以,.
以为原点,,,所在直线分别为轴、轴,轴,建立如图所示的空间直角坐标系,
则,0,,,0,,,2,,,2,,,0,,,1,,
所以.
设平面的一个法向量为,
则,即
取,则,.
所以 是平面的一个法向量.
因为,则,又平面,
所以平面.
(2)由(1)可知,,
又因为,平面,所以平面.
所以 是平面的一个法向量.
设平面与平面的夹角为,
则,
所以平面与平面夹角的余弦值为.
【详解】(1)解:由题知 解得 ,
椭圆的方程为.
(2)将代入椭圆方程,得,
又直线与椭圆有两个交点,,解得.
设,则.
若以为直径的圆过点,则.
又,
.
而,
,
,
,
解得,满足,故.
22.【详解】(1)因为
则,即,所以,经检验符合题意
(2).
当时,,所以在上单调递增;
当时,令,解得,
当时,;
当时,;
所以在上单调递增,在上单调递减;
(3)的定义域为,若恒成立,则恒成立,
即恒成立,
令,只需,又,
令得,
时,,则单调递增;
时,,则单调递减;
所以,解得:;
同课章节目录
