苏教版六年级数学下册第六单元正比例和反比例单元检测(含答案)
文档属性
| 名称 | 苏教版六年级数学下册第六单元正比例和反比例单元检测(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
苏教版六年级数学下册第六单元正比例和反比例单元检测
一、单选题( 10分)
1.圆锥的底面半径一定,这个圆锥的体积与它的高的关系( )。
A.成正比例 B.成反比例 C.不成比例 D.无法判断
2.下列每组相关联的两个量的关系可以用下图表示的是( )。
A.六(1)班今天的出勤人数和缺勤人数B.路程一定时,速度和时间
C.圆的周长与该圆的直径 D.圆柱的体积和圆锥的体积
3.下面成正比例关系的是( )。
A.班级总人数一定,男生人数和女生人数。
B.速度一定,路程和时间。
C.总钱数一定,钢笔单价和买的支数。
D.圆的面积和半径。
4.某人造地球卫星在空中绕地球运行的周数和所用时间的关系如图,运行的周数和所用的时间( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
5.用一块橡皮泥捏不同的圆柱体,圆柱体的底面积和高( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
二、判断题( 10分)
6.小麦每公顷产量一定,小麦的总产量与公顷数成正比例关系。( )
7.做20道计算题做对的题数和做错的题数既不成正比例,也不成反比例。( )
8. (x、y≠0),x和y成反比例。( )
9.图上距离一定,实际距离和比例尺成反比例关系。( )
10.3m-2n=0,m和n成正比例。( )
三、填空题( 17分)
11.如果y =8x,那么x和y成 比例,原因是 。
12.面积一定,平行四边形的底和高成 比例。
13.包装一批糖果, 一定,每袋装的颗数和所装袋数成反比例。
14.若x= y,那么x和y成 比例关系;若 = ,那么x和y成 比例关系。
15.三角形的底一定,三角形的面积和高成 比例。
16.已知7x=8y(x、y都不为0),x和y成 比例,已知 ,x和y成 比例。
17.在上午某一时刻,身高1.7米的小桐在地面上的影子长3.4米,小桐测得校园中旗杆在地面上的影子长16米,还有2米长的影子落在墙上,由此可知,旗杆高 米。
18.购置8万元电脑,电脑的单价和数量成 比例。
19.三角形面积一定,底和高成 比例。
20.如果2A= B,那么A:B= : ,A与B成 比例。
21.用数学的眼光来看成语“立竿见影”,是应用了本学期所学的 知识。即同一时间,同一地点,竿高和影长成 比例。
四、解答题( 38分)
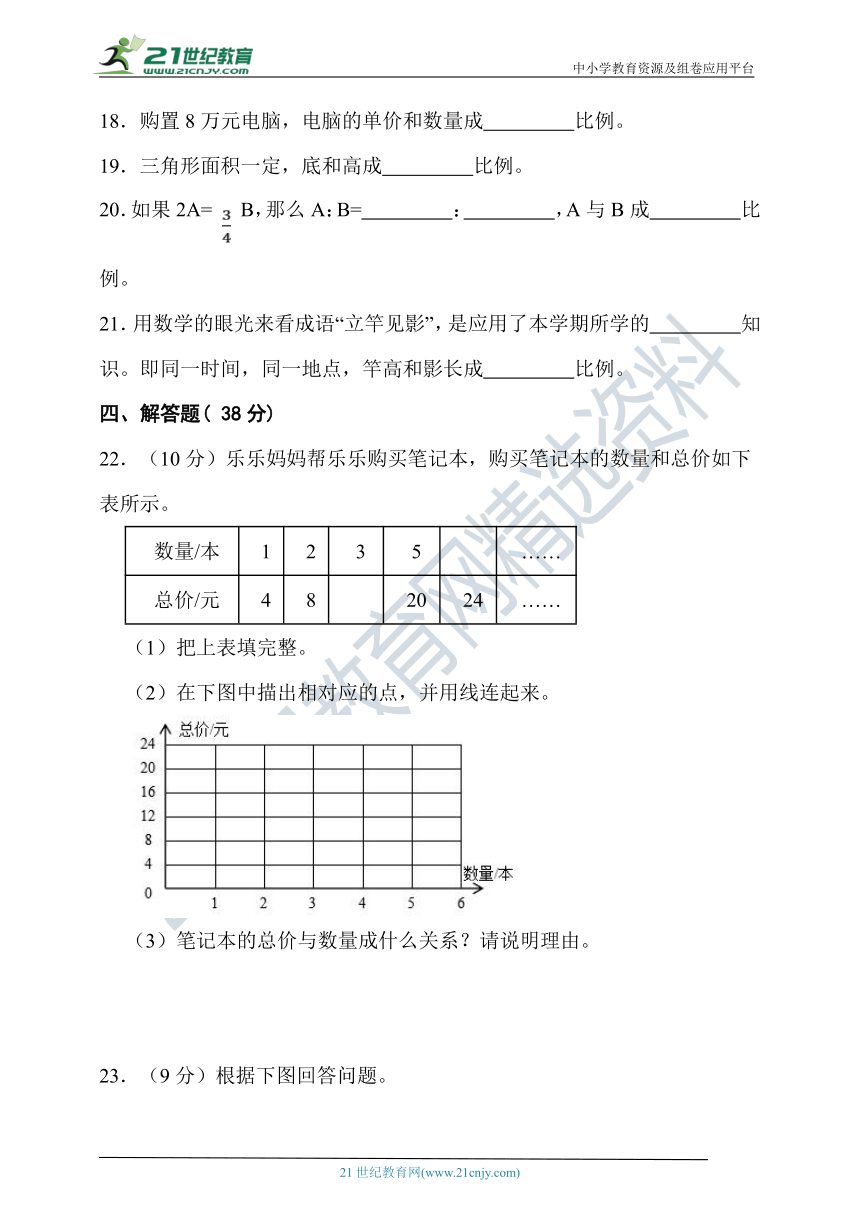
22.(10分)乐乐妈妈帮乐乐购买笔记本,购买笔记本的数量和总价如下表所示。
数量/本 1 2 3 5 ……
总价/元 4 8 20 24 ……
(1)把上表填完整。
(2)在下图中描出相对应的点,并用线连起来。
(3)笔记本的总价与数量成什么关系?请说明理由。
23.(9分)根据下图回答问题。
(1)图中的A点表示1小时行80千米,B点表示5小时行 千米。
(2)图中所描的点在一条直线上吗?
(3)根据图像判断,这辆汽车2.5 小时行驶多少千米?行驶440千米需要多少小时?
24.(13分)下表是鸵鸟奔跑的距离与所用时间的关系表,看表回答下列问题,
距离/千米 70 140 210 280 350 420
时间/时 1 2 3 4 5 6
(1)(5分)把上表中距离和时间所对应的点描在方格纸上,再顺次连接。
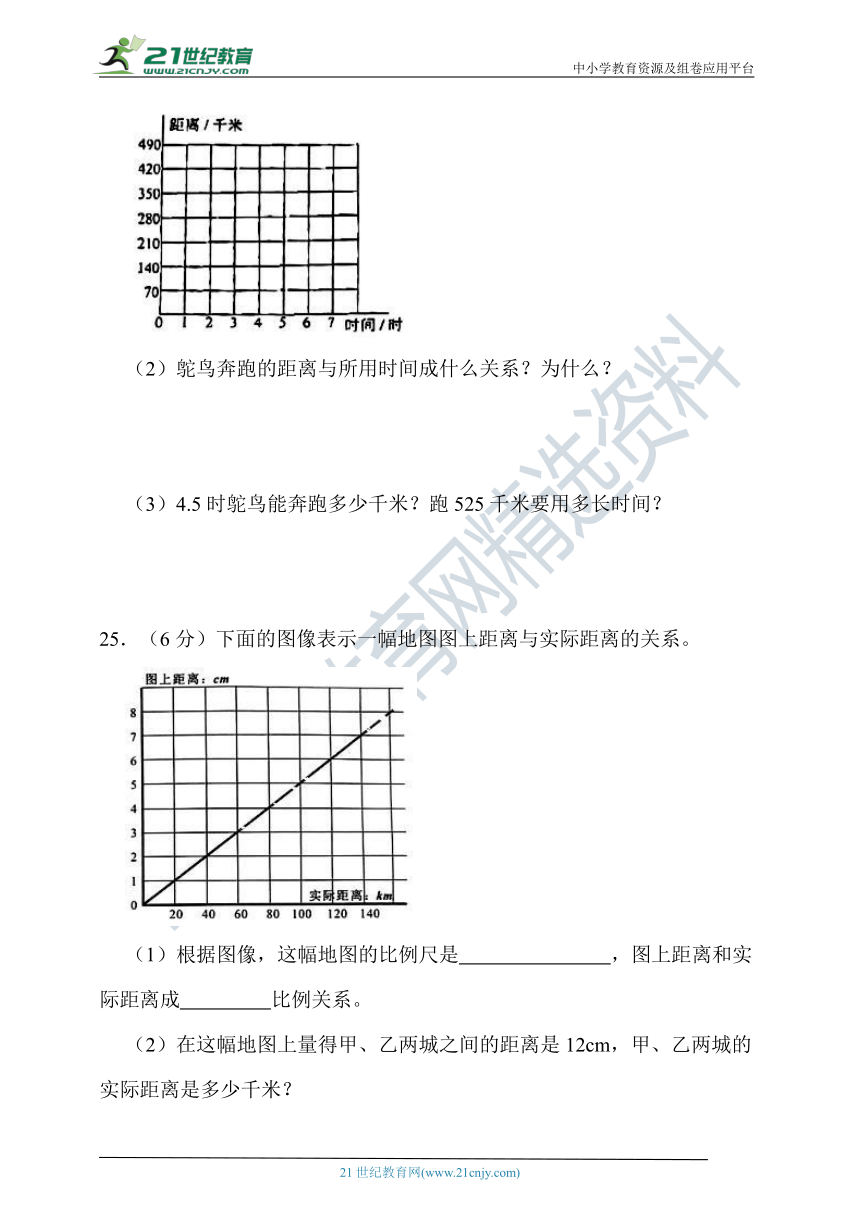
(2)鸵鸟奔跑的距离与所用时间成什么关系?为什么?
(3)4.5时鸵鸟能奔跑多少千米?跑525千米要用多长时间?
25.(6分)下面的图像表示一幅地图图上距离与实际距离的关系。
(1)根据图像,这幅地图的比例尺是 ,图上距离和实际距离成 比例关系。
(2)在这幅地图上量得甲、乙两城之间的距离是12cm,甲、乙两城的实际距离是多少千米?
五、应用题(共5题;共25分)
26.(5分)一运输队为云南干旱灾区抢运水,一次全部运完。如果用载重量是10吨的车20辆即可运完。如果用载重量是8吨的车,多少辆可以一次运完?
27.(5分)在春游活动中,我班共创建了8个活动小组,每组5人。现因活动需要每组增加5人,则有几个小组?
28.(5分)一间房子要用方砖铺地,用边长5分米的方砖需用2000块,如果改用边长是4分米的方砖,需用多少块?
29.(5分)印刷厂用一批纸装订英语练习本.如果每本36页,能订4000本,如果每本32页,能订多少本?
30.(5分)一辆汽车从甲地开往乙地,前2小时行驶了100千米.照这样的速度,再行6小时到达乙地,甲、乙两地相距多远?
答案
1.C
2.C
3.B
4.A
5.B
6.√
7.√
8.√
9.√
10.√
11.正;x和y的商一定
12.反
13.糖果的总颗数
14.正;反
15.正
16.正;反
17.10
18.反
19.反
20.3;8;正
21.比例;正
22.(1)解:
数量/本 1 2 3 5 6 ……
总价/元 4 8 12 20 24 ……
(2)解:如图:
(3)解:成正比例关系。数量与总价,总价随着数量的变化而变化,但是它们的单价(比值)不变,因此笔记本的总价与数量成正比例关系。
23.(1)400
(2)解:在一条直线上
(3)解:80×2.5=200(千米)
440÷80=5.5(小时)
答:这辆汽车2.5 小时行驶200千米,行驶440千米需要5.5小时。
24.(1)解:
(2)答: 鸵鸟奔跑的距离与所用时间成 成正比例,因为距离÷时间=70(一定),商一定,距离与时间成正比例关系。
(3)解:70÷1×4.5
=70×4.5
=315(千米)
525÷ (70÷1)
=525÷70
=7.5(小时)
答:4.5小时鸵鸟能奔跑315千米,跑525 km用7.5小时。
25.(1)1:2000000;正
(2)解:12×20=240(千米)
答:甲、乙两城的实际距离是240千米。
26.解:设x辆可以一次运完.
8x=10×20
x=200÷8
x=25
答:25辆可以一次运完.
27.解:设现在有x个小组,
(5+5)x=8×5
x=40÷10
x=4
答:则现在有4个小组.
28.解:设需用x块,
4×4×x=5×5×2000
16x=25×2000
16x÷16=50000÷16
x=3125
答:需用3125块
29.解:设可以装订x本,
32x=36×4000,
32x=144000,
x=4500,
答:可以装订4500本.
30.解:设甲、乙两地相距x千米,
100:2=x:(6+2),
2 x =100×(6+2),
2 x =800,
x =400;
答:甲、乙两地相距400千米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
苏教版六年级数学下册第六单元正比例和反比例单元检测
一、单选题( 10分)
1.圆锥的底面半径一定,这个圆锥的体积与它的高的关系( )。
A.成正比例 B.成反比例 C.不成比例 D.无法判断
2.下列每组相关联的两个量的关系可以用下图表示的是( )。
A.六(1)班今天的出勤人数和缺勤人数B.路程一定时,速度和时间
C.圆的周长与该圆的直径 D.圆柱的体积和圆锥的体积
3.下面成正比例关系的是( )。
A.班级总人数一定,男生人数和女生人数。
B.速度一定,路程和时间。
C.总钱数一定,钢笔单价和买的支数。
D.圆的面积和半径。
4.某人造地球卫星在空中绕地球运行的周数和所用时间的关系如图,运行的周数和所用的时间( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
5.用一块橡皮泥捏不同的圆柱体,圆柱体的底面积和高( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
二、判断题( 10分)
6.小麦每公顷产量一定,小麦的总产量与公顷数成正比例关系。( )
7.做20道计算题做对的题数和做错的题数既不成正比例,也不成反比例。( )
8. (x、y≠0),x和y成反比例。( )
9.图上距离一定,实际距离和比例尺成反比例关系。( )
10.3m-2n=0,m和n成正比例。( )
三、填空题( 17分)
11.如果y =8x,那么x和y成 比例,原因是 。
12.面积一定,平行四边形的底和高成 比例。
13.包装一批糖果, 一定,每袋装的颗数和所装袋数成反比例。
14.若x= y,那么x和y成 比例关系;若 = ,那么x和y成 比例关系。
15.三角形的底一定,三角形的面积和高成 比例。
16.已知7x=8y(x、y都不为0),x和y成 比例,已知 ,x和y成 比例。
17.在上午某一时刻,身高1.7米的小桐在地面上的影子长3.4米,小桐测得校园中旗杆在地面上的影子长16米,还有2米长的影子落在墙上,由此可知,旗杆高 米。
18.购置8万元电脑,电脑的单价和数量成 比例。
19.三角形面积一定,底和高成 比例。
20.如果2A= B,那么A:B= : ,A与B成 比例。
21.用数学的眼光来看成语“立竿见影”,是应用了本学期所学的 知识。即同一时间,同一地点,竿高和影长成 比例。
四、解答题( 38分)
22.(10分)乐乐妈妈帮乐乐购买笔记本,购买笔记本的数量和总价如下表所示。
数量/本 1 2 3 5 ……
总价/元 4 8 20 24 ……
(1)把上表填完整。
(2)在下图中描出相对应的点,并用线连起来。
(3)笔记本的总价与数量成什么关系?请说明理由。
23.(9分)根据下图回答问题。
(1)图中的A点表示1小时行80千米,B点表示5小时行 千米。
(2)图中所描的点在一条直线上吗?
(3)根据图像判断,这辆汽车2.5 小时行驶多少千米?行驶440千米需要多少小时?
24.(13分)下表是鸵鸟奔跑的距离与所用时间的关系表,看表回答下列问题,
距离/千米 70 140 210 280 350 420
时间/时 1 2 3 4 5 6
(1)(5分)把上表中距离和时间所对应的点描在方格纸上,再顺次连接。
(2)鸵鸟奔跑的距离与所用时间成什么关系?为什么?
(3)4.5时鸵鸟能奔跑多少千米?跑525千米要用多长时间?
25.(6分)下面的图像表示一幅地图图上距离与实际距离的关系。
(1)根据图像,这幅地图的比例尺是 ,图上距离和实际距离成 比例关系。
(2)在这幅地图上量得甲、乙两城之间的距离是12cm,甲、乙两城的实际距离是多少千米?
五、应用题(共5题;共25分)
26.(5分)一运输队为云南干旱灾区抢运水,一次全部运完。如果用载重量是10吨的车20辆即可运完。如果用载重量是8吨的车,多少辆可以一次运完?
27.(5分)在春游活动中,我班共创建了8个活动小组,每组5人。现因活动需要每组增加5人,则有几个小组?
28.(5分)一间房子要用方砖铺地,用边长5分米的方砖需用2000块,如果改用边长是4分米的方砖,需用多少块?
29.(5分)印刷厂用一批纸装订英语练习本.如果每本36页,能订4000本,如果每本32页,能订多少本?
30.(5分)一辆汽车从甲地开往乙地,前2小时行驶了100千米.照这样的速度,再行6小时到达乙地,甲、乙两地相距多远?
答案
1.C
2.C
3.B
4.A
5.B
6.√
7.√
8.√
9.√
10.√
11.正;x和y的商一定
12.反
13.糖果的总颗数
14.正;反
15.正
16.正;反
17.10
18.反
19.反
20.3;8;正
21.比例;正
22.(1)解:
数量/本 1 2 3 5 6 ……
总价/元 4 8 12 20 24 ……
(2)解:如图:
(3)解:成正比例关系。数量与总价,总价随着数量的变化而变化,但是它们的单价(比值)不变,因此笔记本的总价与数量成正比例关系。
23.(1)400
(2)解:在一条直线上
(3)解:80×2.5=200(千米)
440÷80=5.5(小时)
答:这辆汽车2.5 小时行驶200千米,行驶440千米需要5.5小时。
24.(1)解:
(2)答: 鸵鸟奔跑的距离与所用时间成 成正比例,因为距离÷时间=70(一定),商一定,距离与时间成正比例关系。
(3)解:70÷1×4.5
=70×4.5
=315(千米)
525÷ (70÷1)
=525÷70
=7.5(小时)
答:4.5小时鸵鸟能奔跑315千米,跑525 km用7.5小时。
25.(1)1:2000000;正
(2)解:12×20=240(千米)
答:甲、乙两城的实际距离是240千米。
26.解:设x辆可以一次运完.
8x=10×20
x=200÷8
x=25
答:25辆可以一次运完.
27.解:设现在有x个小组,
(5+5)x=8×5
x=40÷10
x=4
答:则现在有4个小组.
28.解:设需用x块,
4×4×x=5×5×2000
16x=25×2000
16x÷16=50000÷16
x=3125
答:需用3125块
29.解:设可以装订x本,
32x=36×4000,
32x=144000,
x=4500,
答:可以装订4500本.
30.解:设甲、乙两地相距x千米,
100:2=x:(6+2),
2 x =100×(6+2),
2 x =800,
x =400;
答:甲、乙两地相距400千米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
