6.4.3余弦定理、正弦定理第1课时余弦定理 课件(共15张PPT)
文档属性
| 名称 | 6.4.3余弦定理、正弦定理第1课时余弦定理 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 670.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 10:35:39 | ||
图片预览




文档简介
(共15张PPT)
6.4.3 余弦定理、正弦定理
第1课时 余弦定理
第六章 平面向量及其应用
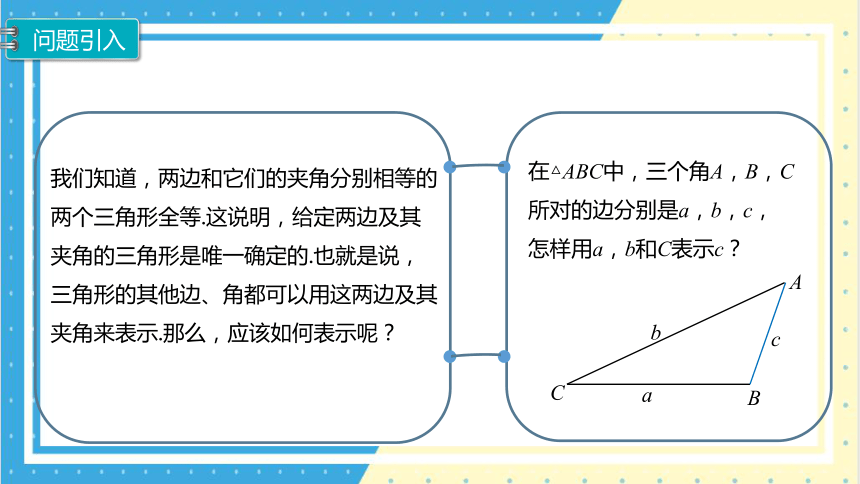
问题引入
我们知道,两边和它们的夹角分别相等的两个三角形全等.这说明,给定两边及其
夹角的三角形是唯一确定的.也就是说,
三角形的其他边、角都可以用这两边及其夹角来表示.那么,应该如何表示呢?
在△ABC中,三个角A,B,C所对的边分别是a,b,c,
怎样用a,b和C表示c?
A
a
c
b
B
C
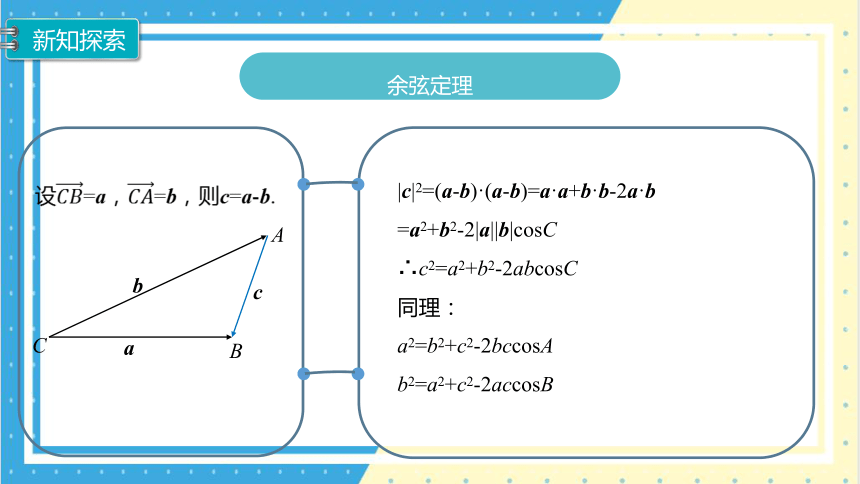
新知探索
余弦定理
A
a
c
b
B
C
设=a,=b,则c=a-b.
|c|2=(a-b)·(a-b)=a·a+b·b-2a·b
=a2+b2-2|a||b|cosC
∴c2=a2+b2-2abcosC
同理:
a2=b2+c2-2bccosA
b2=a2+c2-2accosB
已知钝角△ABC,设角A,B,C的对边分别为a,b,c,试借助三角函数定义
用a,b,C表示边c.
新知探索
余弦定理
解 不妨设A为钝角.
如图,作BD⊥CA,交CA延长线于点D.
∴BD=asin C,CD=acos C.
∴AD=CD-CA=acos C-b.
∴c2=BD2+AD2
=a2sin2C+(acos C-b)2
=a2sin2C+a2cos2C+b2-2abcos C
=a2+b2-2abcos C.
如图,以A为原点,边AB所在直线为x轴建立平面直角坐标系.
则A(0,0),B(c,0),C(bcos A,bsin A),
∴BC2=b2cos2A-2bccos A+c2+b2sin2A,
即a2=b2+c2-2bccos A.
同理可证b2=c2+a2-2cacos B,
c2=a2+b2-2abcos C.
新知探索
余弦定理
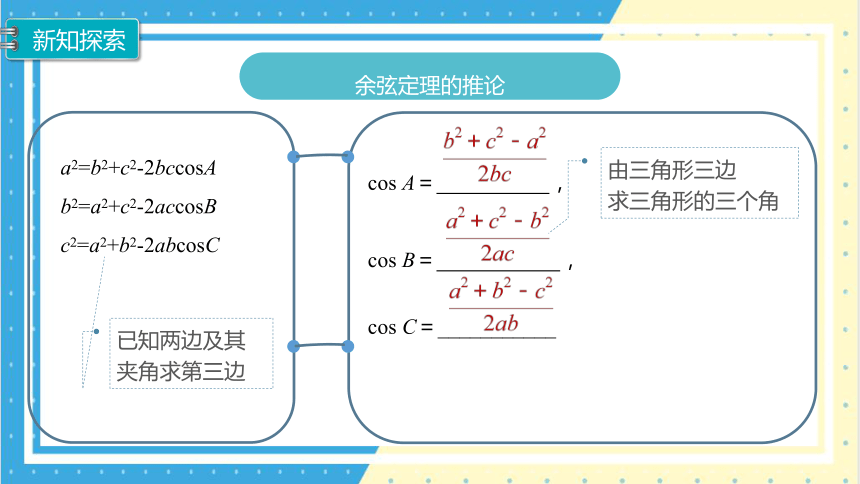
新知探索
余弦定理的推论
a2=b2+c2-2bccosA
b2=a2+c2-2accosB
c2=a2+b2-2abcosC
cos A= ,
cos B= ,
cos C=___________
已知两边及其夹角求第三边
由三角形三边
求三角形的三个角
典例精析
题型一:用余弦定理解三角形
解 根据余弦定理,得c2=a2+b2-2abcos C
例3 在△ABC中,a=,b=,A=30°,则c等于 ( )
A.2 B.
C.2或 D.以上都不对
解 由余弦定理可得a2=b2+c2-2bccos A,
又因为a=,b=,A=30°,
所以()2=()2+c2-2××c×cos30°
整理得c2-3c+10=0,解得c=或2.
典例精析
题型三:判断三角形的形状
跟踪练习
1.在△ABC中,bcos C+ccos B=2b,则 =
A. B. C. D.2
解 由已知,
b×+c×=2b,
化为a=2b,即=.
跟踪练习
∴在△ABD中,有BD2=AB2+AD2-2AB·ADcos∠BAD,
跟踪练习
3.在△ABC中,若b(a-ccos B)=a(b-ccos A),
判断△ABC的形状.
解 由余弦定理,
得b(a-c×)=a(b-c×)
整理得(a2+b2-c2)b2=(a2+b2-c2)a2,
即(a2-b2)(a2+b2-c2)=0,
所以a2+b2-c2=0或a2=b2.
所以a2+b2=c2或a=b.
故△ABC为直角三角形或等腰三角形.
定理
形式
定理证明
定理应用
角为余弦、边为二次
向量法、转化为直角三角形、坐标法
边角互化
课堂小结
本节内容结束
6.4.3 余弦定理、正弦定理
第1课时 余弦定理
第六章 平面向量及其应用
问题引入
我们知道,两边和它们的夹角分别相等的两个三角形全等.这说明,给定两边及其
夹角的三角形是唯一确定的.也就是说,
三角形的其他边、角都可以用这两边及其夹角来表示.那么,应该如何表示呢?
在△ABC中,三个角A,B,C所对的边分别是a,b,c,
怎样用a,b和C表示c?
A
a
c
b
B
C
新知探索
余弦定理
A
a
c
b
B
C
设=a,=b,则c=a-b.
|c|2=(a-b)·(a-b)=a·a+b·b-2a·b
=a2+b2-2|a||b|cosC
∴c2=a2+b2-2abcosC
同理:
a2=b2+c2-2bccosA
b2=a2+c2-2accosB
已知钝角△ABC,设角A,B,C的对边分别为a,b,c,试借助三角函数定义
用a,b,C表示边c.
新知探索
余弦定理
解 不妨设A为钝角.
如图,作BD⊥CA,交CA延长线于点D.
∴BD=asin C,CD=acos C.
∴AD=CD-CA=acos C-b.
∴c2=BD2+AD2
=a2sin2C+(acos C-b)2
=a2sin2C+a2cos2C+b2-2abcos C
=a2+b2-2abcos C.
如图,以A为原点,边AB所在直线为x轴建立平面直角坐标系.
则A(0,0),B(c,0),C(bcos A,bsin A),
∴BC2=b2cos2A-2bccos A+c2+b2sin2A,
即a2=b2+c2-2bccos A.
同理可证b2=c2+a2-2cacos B,
c2=a2+b2-2abcos C.
新知探索
余弦定理
新知探索
余弦定理的推论
a2=b2+c2-2bccosA
b2=a2+c2-2accosB
c2=a2+b2-2abcosC
cos A= ,
cos B= ,
cos C=___________
已知两边及其夹角求第三边
由三角形三边
求三角形的三个角
典例精析
题型一:用余弦定理解三角形
解 根据余弦定理,得c2=a2+b2-2abcos C
例3 在△ABC中,a=,b=,A=30°,则c等于 ( )
A.2 B.
C.2或 D.以上都不对
解 由余弦定理可得a2=b2+c2-2bccos A,
又因为a=,b=,A=30°,
所以()2=()2+c2-2××c×cos30°
整理得c2-3c+10=0,解得c=或2.
典例精析
题型三:判断三角形的形状
跟踪练习
1.在△ABC中,bcos C+ccos B=2b,则 =
A. B. C. D.2
解 由已知,
b×+c×=2b,
化为a=2b,即=.
跟踪练习
∴在△ABD中,有BD2=AB2+AD2-2AB·ADcos∠BAD,
跟踪练习
3.在△ABC中,若b(a-ccos B)=a(b-ccos A),
判断△ABC的形状.
解 由余弦定理,
得b(a-c×)=a(b-c×)
整理得(a2+b2-c2)b2=(a2+b2-c2)a2,
即(a2-b2)(a2+b2-c2)=0,
所以a2+b2-c2=0或a2=b2.
所以a2+b2=c2或a=b.
故△ABC为直角三角形或等腰三角形.
定理
形式
定理证明
定理应用
角为余弦、边为二次
向量法、转化为直角三角形、坐标法
边角互化
课堂小结
本节内容结束
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
