1.2动量定理 课件(第1课时)(共19张PPT)
文档属性
| 名称 | 1.2动量定理 课件(第1课时)(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-05-24 11:06:14 | ||
图片预览






文档简介
(共19张PPT)
第一章 动量守恒定律
第二节 动量定理
一、碰撞的力
两个物体碰撞时,彼此间会受到力的作用,某物体动量的变化和它所受的力到底有怎样的关系呢?
船体周围的轮胎有什么用?
0
F
mv
安全气囊在撞击过程中的作用
一、碰撞的力
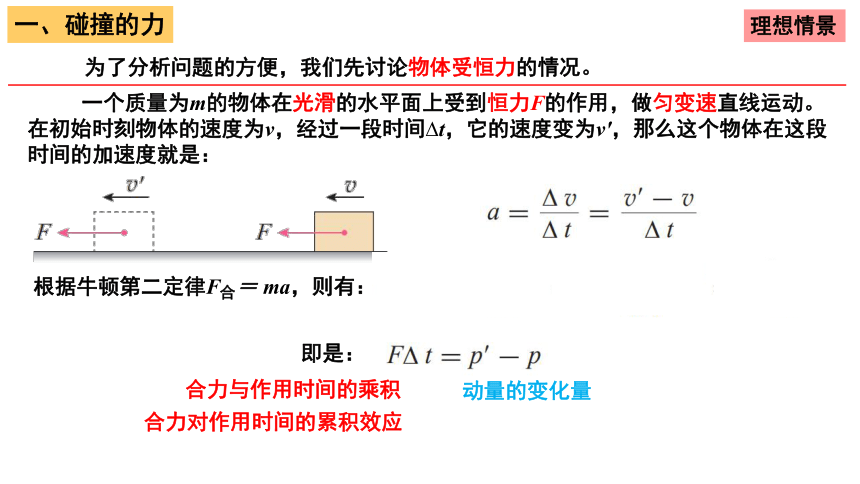
为了分析问题的方便,我们先讨论物体受恒力的情况。
一个质量为m的物体在光滑的水平面上受到恒力F的作用,做匀变速直线运动。在初始时刻物体的速度为v,经过一段时间 t,它的速度变为v′,那么这个物体在这段时间的加速度就是:
根据牛顿第二定律F = ma,则有:
即是:
动量的变化量
合力与作用时间的乘积
合力对作用时间的累积效应
理想情景
合
真实情景1
一、碰撞的力
为了分析问题的方便,我们先讨论物体受恒力的情况。
一个质量为m的物体在粗糙的水平面上受到恒力F的作用,动摩擦因数为μ,做匀变速直线运动。在初始时刻物体的速度为v,经过一段时间 t,它的速度变为v′,那么物体在这段时间的加速度就是:
f
f
根据牛顿第二定律F = ma,则有:
合
即是:
动量的变化量
合力与作用时间的乘积
合力对作用时间的累积效应
真实情景2
一、碰撞的力
为了获得更加普遍的结论,我们现在讨论物体受变力的情况。
一个质量为m的物体在粗糙的水平面上受到变力F的作用,动摩擦因数为μ,做变加速直线运动。在初始时刻物体的速度为v,经过一段时间 t,它的速度变为v′,那么物体在这段时间内:
f
f
将所有方程累加起来,可得:
动量的变化量
合力与作用时间的乘积
合力对作用时间的累积效应
t
F
将这段时间分为很多份小时间,
F1
Fn
每一份时间内可认为是匀加速运动,则由真实情景1有:
一、碰撞的力
通过上述3种不同的情景,我们可以得到:
F t 这个物理量反映了力的作用对时间的累积效应。物理学中把力与力的作用时间的乘积叫作力的冲量(impulse),用字母I 表示冲量,则:
I =F t
冲量的单位是:牛秒,符号是N·S。
冲量
1. 冲量是矢量:方向由力的方向决定;若为恒定方向的力,则冲量的方向与这个力的方向相同。
2. 冲量是过程量,反映了力对时间的积累效应。
例题1. 在倾角α=37°的斜面上,有一质量为5 kg的物体沿斜面滑下,物体与斜面间的动摩擦因数μ=0.2,求物体下滑2 s的时间内,物体所受各力的冲量.(g取10 m/s2)
mg
FN
Ff
二、冲量
通过上述3种不同的情景,我们可以得到:
I = F t
例题2. 一质量m = 2 kg的物体处于静止,经t = 5 s,求
(1)重力的冲量:
(2)支持力的冲量:
(3)合外力的冲量:
合力的冲量计算:
(1)先算出各个力的冲量后,再求各冲量矢量和,
(2)先算合力再用I合=F合·Δt,求合力的冲量。
(各个力的作用时间相同)
mg
N
二、冲量
通过上述3种不同的情景,我们可以得到:
I = F t
一、碰撞的力
通过上述3种不同的情景,我们可以得到:
F t 这个物理量反映了力的作用对时间的累积效应。物理学中把力与力的作用时间的乘积叫作力的冲量(impulse),用字母I 表示冲量,则:
I =F t
冲量的单位是:牛秒,符号是N·S。
有了冲量的概念,上述3种不同的情景可以统一写为:
I = p ′- p
物体在一个过程中所受合外力的冲量等于它在这个过程始末的动量变化量。这个关系叫作动量定理(theorem of momentum)。
合
动量定理
二、冲量
通过上述3种不同的情景,我们可以得到:
I = F t
方向与力的方向一致;
1. 求恒力的冲量:
(1)若力的方向不变,大小变化:
平均力的冲量:
由F- t 图求解:
2. 求变力的冲量:
I = F t
t
F
IF = S
面积
(2)若力的方向变化,或大小方向均变化:
由动量定理求解:
例如,匀速圆周运动的向心力
例如,对单摆摆球的拉力
例如,求地面给鸡蛋的冲击力
不能用I=Ft 求解
方向由力的方向决定,但不是力的方向
I = p ′- p
合
三、动量定理
通过上述3种不同的情景,我们可以得到:
物体在一个过程中所受合外力的冲量等于它在这个过程始末的动量变化量。这个关系叫作动量定理(theorem of momentum)。
I = p ′- p
合
1. 动量定理不仅适用于恒力,也适用于随时间变化的变力;对于变力,动量定理中的F应理解为变力在作用时间内的平均值;
2. 动量定理不仅可以解决匀变速直线运动的问题,还可以解决曲线运动中的有关问题,将较难的计算问题转化为较易的计算问题;
3. 动量定理不仅适用于宏观低速物体,也适用于微观现象和变速运动问题。
动量定理的优点:
适用范围:
不考虑中间过程,只考虑初末状态。
4. 动量定理是矢量式;
5. 合外力的冲量方向与速度变化量的方向一致。
三、动量定理
通过上述3种不同的情景,我们可以得到:
I = p ′- p
合
例题3. 一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为45m/s,设球棒与垒球的作用时间为0.01s。球棒对垒球的平均作用力是多大?
动量定理的应用步骤
1、确定研究对象:一般为单个物体;
4、选定正方向,确定在物理过程中研究对象的动量的变化;
5、根据动量定理列方程,统一单位后代入数据求解。
2、明确物理过程:受力分析,求出合外力的冲量;
3、明确研究对象的初末状态及相应的动量;
三、动量定理
通过上述3种不同的情景,我们可以得到:
I = p ′- p
合
四、动量定理的应用
通过上述3种不同的情景,我们可以得到:
I = p ′- p
合
传接球时为何不自觉地弯曲手臂?
四、动量定理的应用
通过上述3种不同的情景,我们可以得到:
I = p ′- p
合
四、动量定理的应用
通过上述3种不同的情景,我们可以得到:
I = p ′- p
合
1、解释有关现象
越长,
一定,
越短,
则F越小。
则F越大。
一定,
例题1. 若一个50 g的鸡蛋从20m坠下,与地面的撞击时间约为0.001s,则该鸡蛋对地面产生的冲击力约为( )
A.10 N B.102 N C.103 N D.104 N
C
思考:若地面平铺一层海绵,使得撞击时间变为0.1s,冲击力?
10N
—— 缓冲作用
四、动量定理的应用
通过上述3种不同的情景,我们可以得到:
I = p ′- p
合
例题2. 质量为60 kg的建筑工人,不慎从高空跌下,幸好弹性安全带的保护使他悬挂起来.已知弹性安全带的缓冲时间是1.5 s,安全带自然长度为5 m,g取10 m/s2,求安全带所受的平均冲力的大小?
v
0
(规定向下为正方向)
F = 1000N
解:
刚刚伸直
最低点
冲量
功
区
别
公式
标矢性
意义
正负
作用效果
单位
某个力对物体有冲量,不一定做功;某个力对物体做了功,一定有冲量。
N·S
I=Ft
W=Fxcos θ
矢量
标量
N·m 或(J)
力对时间的积累, 对应一段时间
在F-t图像中可以用面积表示
力对位移的积累, 对应一段位移
在F-x图像中可以用面积表示
正负表示与正方向相同或相反
正负表示动力做功或阻力做功
改变物体的动量
改变物体的动能
F
t
O
F
t
x
F
O
F
x
五、冲量与功
例题3.一铁块压着一纸条放在水平桌面上,当以速度v抽出纸条后,铁块掉在地上的P点.若以2v速度抽出纸条,则铁块落地点为( )
A.仍在P点
B.在P点左边
C.在P点右边不远处
D.在P点右边原水平位移的两倍处
B
四、动量定理的应用
通过上述3种不同的情景,我们可以得到:
I = p ′- p
合
第一章 动量守恒定律
第二节 动量定理
一、碰撞的力
两个物体碰撞时,彼此间会受到力的作用,某物体动量的变化和它所受的力到底有怎样的关系呢?
船体周围的轮胎有什么用?
0
F
mv
安全气囊在撞击过程中的作用
一、碰撞的力
为了分析问题的方便,我们先讨论物体受恒力的情况。
一个质量为m的物体在光滑的水平面上受到恒力F的作用,做匀变速直线运动。在初始时刻物体的速度为v,经过一段时间 t,它的速度变为v′,那么这个物体在这段时间的加速度就是:
根据牛顿第二定律F = ma,则有:
即是:
动量的变化量
合力与作用时间的乘积
合力对作用时间的累积效应
理想情景
合
真实情景1
一、碰撞的力
为了分析问题的方便,我们先讨论物体受恒力的情况。
一个质量为m的物体在粗糙的水平面上受到恒力F的作用,动摩擦因数为μ,做匀变速直线运动。在初始时刻物体的速度为v,经过一段时间 t,它的速度变为v′,那么物体在这段时间的加速度就是:
f
f
根据牛顿第二定律F = ma,则有:
合
即是:
动量的变化量
合力与作用时间的乘积
合力对作用时间的累积效应
真实情景2
一、碰撞的力
为了获得更加普遍的结论,我们现在讨论物体受变力的情况。
一个质量为m的物体在粗糙的水平面上受到变力F的作用,动摩擦因数为μ,做变加速直线运动。在初始时刻物体的速度为v,经过一段时间 t,它的速度变为v′,那么物体在这段时间内:
f
f
将所有方程累加起来,可得:
动量的变化量
合力与作用时间的乘积
合力对作用时间的累积效应
t
F
将这段时间分为很多份小时间,
F1
Fn
每一份时间内可认为是匀加速运动,则由真实情景1有:
一、碰撞的力
通过上述3种不同的情景,我们可以得到:
F t 这个物理量反映了力的作用对时间的累积效应。物理学中把力与力的作用时间的乘积叫作力的冲量(impulse),用字母I 表示冲量,则:
I =F t
冲量的单位是:牛秒,符号是N·S。
冲量
1. 冲量是矢量:方向由力的方向决定;若为恒定方向的力,则冲量的方向与这个力的方向相同。
2. 冲量是过程量,反映了力对时间的积累效应。
例题1. 在倾角α=37°的斜面上,有一质量为5 kg的物体沿斜面滑下,物体与斜面间的动摩擦因数μ=0.2,求物体下滑2 s的时间内,物体所受各力的冲量.(g取10 m/s2)
mg
FN
Ff
二、冲量
通过上述3种不同的情景,我们可以得到:
I = F t
例题2. 一质量m = 2 kg的物体处于静止,经t = 5 s,求
(1)重力的冲量:
(2)支持力的冲量:
(3)合外力的冲量:
合力的冲量计算:
(1)先算出各个力的冲量后,再求各冲量矢量和,
(2)先算合力再用I合=F合·Δt,求合力的冲量。
(各个力的作用时间相同)
mg
N
二、冲量
通过上述3种不同的情景,我们可以得到:
I = F t
一、碰撞的力
通过上述3种不同的情景,我们可以得到:
F t 这个物理量反映了力的作用对时间的累积效应。物理学中把力与力的作用时间的乘积叫作力的冲量(impulse),用字母I 表示冲量,则:
I =F t
冲量的单位是:牛秒,符号是N·S。
有了冲量的概念,上述3种不同的情景可以统一写为:
I = p ′- p
物体在一个过程中所受合外力的冲量等于它在这个过程始末的动量变化量。这个关系叫作动量定理(theorem of momentum)。
合
动量定理
二、冲量
通过上述3种不同的情景,我们可以得到:
I = F t
方向与力的方向一致;
1. 求恒力的冲量:
(1)若力的方向不变,大小变化:
平均力的冲量:
由F- t 图求解:
2. 求变力的冲量:
I = F t
t
F
IF = S
面积
(2)若力的方向变化,或大小方向均变化:
由动量定理求解:
例如,匀速圆周运动的向心力
例如,对单摆摆球的拉力
例如,求地面给鸡蛋的冲击力
不能用I=Ft 求解
方向由力的方向决定,但不是力的方向
I = p ′- p
合
三、动量定理
通过上述3种不同的情景,我们可以得到:
物体在一个过程中所受合外力的冲量等于它在这个过程始末的动量变化量。这个关系叫作动量定理(theorem of momentum)。
I = p ′- p
合
1. 动量定理不仅适用于恒力,也适用于随时间变化的变力;对于变力,动量定理中的F应理解为变力在作用时间内的平均值;
2. 动量定理不仅可以解决匀变速直线运动的问题,还可以解决曲线运动中的有关问题,将较难的计算问题转化为较易的计算问题;
3. 动量定理不仅适用于宏观低速物体,也适用于微观现象和变速运动问题。
动量定理的优点:
适用范围:
不考虑中间过程,只考虑初末状态。
4. 动量定理是矢量式;
5. 合外力的冲量方向与速度变化量的方向一致。
三、动量定理
通过上述3种不同的情景,我们可以得到:
I = p ′- p
合
例题3. 一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为45m/s,设球棒与垒球的作用时间为0.01s。球棒对垒球的平均作用力是多大?
动量定理的应用步骤
1、确定研究对象:一般为单个物体;
4、选定正方向,确定在物理过程中研究对象的动量的变化;
5、根据动量定理列方程,统一单位后代入数据求解。
2、明确物理过程:受力分析,求出合外力的冲量;
3、明确研究对象的初末状态及相应的动量;
三、动量定理
通过上述3种不同的情景,我们可以得到:
I = p ′- p
合
四、动量定理的应用
通过上述3种不同的情景,我们可以得到:
I = p ′- p
合
传接球时为何不自觉地弯曲手臂?
四、动量定理的应用
通过上述3种不同的情景,我们可以得到:
I = p ′- p
合
四、动量定理的应用
通过上述3种不同的情景,我们可以得到:
I = p ′- p
合
1、解释有关现象
越长,
一定,
越短,
则F越小。
则F越大。
一定,
例题1. 若一个50 g的鸡蛋从20m坠下,与地面的撞击时间约为0.001s,则该鸡蛋对地面产生的冲击力约为( )
A.10 N B.102 N C.103 N D.104 N
C
思考:若地面平铺一层海绵,使得撞击时间变为0.1s,冲击力?
10N
—— 缓冲作用
四、动量定理的应用
通过上述3种不同的情景,我们可以得到:
I = p ′- p
合
例题2. 质量为60 kg的建筑工人,不慎从高空跌下,幸好弹性安全带的保护使他悬挂起来.已知弹性安全带的缓冲时间是1.5 s,安全带自然长度为5 m,g取10 m/s2,求安全带所受的平均冲力的大小?
v
0
(规定向下为正方向)
F = 1000N
解:
刚刚伸直
最低点
冲量
功
区
别
公式
标矢性
意义
正负
作用效果
单位
某个力对物体有冲量,不一定做功;某个力对物体做了功,一定有冲量。
N·S
I=Ft
W=Fxcos θ
矢量
标量
N·m 或(J)
力对时间的积累, 对应一段时间
在F-t图像中可以用面积表示
力对位移的积累, 对应一段位移
在F-x图像中可以用面积表示
正负表示与正方向相同或相反
正负表示动力做功或阻力做功
改变物体的动量
改变物体的动能
F
t
O
F
t
x
F
O
F
x
五、冲量与功
例题3.一铁块压着一纸条放在水平桌面上,当以速度v抽出纸条后,铁块掉在地上的P点.若以2v速度抽出纸条,则铁块落地点为( )
A.仍在P点
B.在P点左边
C.在P点右边不远处
D.在P点右边原水平位移的两倍处
B
四、动量定理的应用
通过上述3种不同的情景,我们可以得到:
I = p ′- p
合
