3.2.1古典概型(1)[下学期]
文档属性
| 名称 | 3.2.1古典概型(1)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 231.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-06-09 15:53:00 | ||
图片预览





文档简介
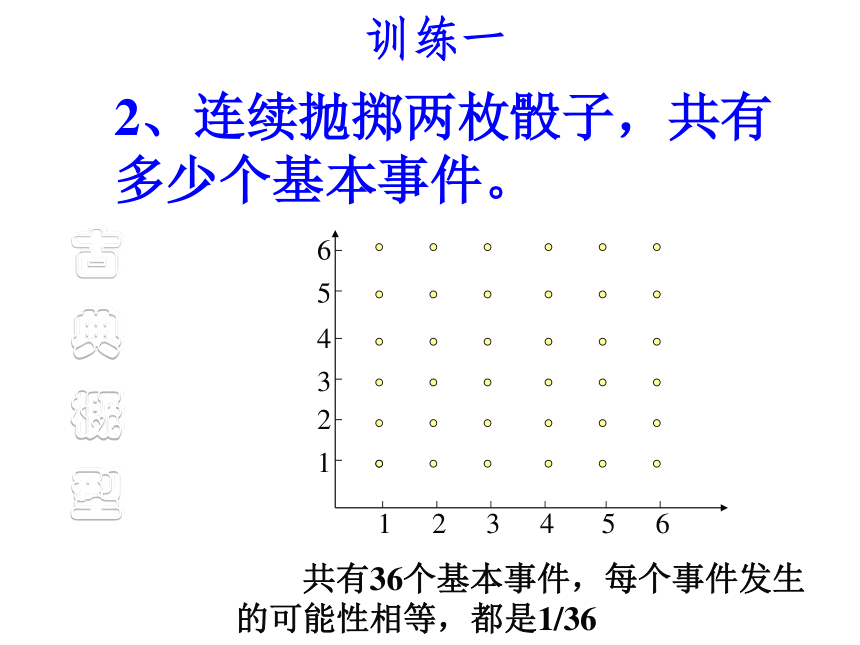
课件13张PPT。 古 典 概 型 事件的构成 古 典 概 型1、掷一枚质地均匀的硬币的试验,可能出现几种不同的结果? 2、掷一枚质地均匀的骰子的试验,可能出现几种不同的结果? 像上面的“正面朝上”、 “正面朝下”;出现“1点”、 “2点”、 “3点”、 “4点”、 “5点”、 “6点”这些随机事件叫做构成试验结果的基本事件。 事件的构成例1 从字母a、b、c、d任意取出两个不同字母的试验中,有哪些基本事件?解:所求的基本事件共有6个: 古 典 概 型A={a, b} B={a, c} C={a, d} D={b, c} E={b, d} F={c, d} 事件的构成基本事件的特点(1)在同一试验中,任何两个基本事件是互斥的;(2)任何事件都可以表示成几个基本事件的和。 古 典 概 型训练一 古 典 概 型1、连续抛掷两枚硬币,写出所有的基本事件。训练一 古 典 概 型2、连续抛掷两枚骰子,共有多少个基本事件。 共有36个基本事件,每个事件发生的可能性相等,都是1/36训练一3、一个袋中装有红、黄、蓝三个大小形状完全相同的球,(1)从中一次性摸出两个球,其中可能出现不同色的两个球的结果。{红,黄},{红,蓝} ,{黄,蓝}(2)从中先后摸出两个球,其中可能出现不同色的两个球的结果。(红,黄),(红,蓝),(黄,蓝) (黄,红),(蓝,红),(蓝,黄) 世纪P73例题1 古 典 概 率我们会发现,以上三个试验有两个共同特征:(1)有限性:在随机试验中,其可能出现的结果有有限个,即只有有限个不同的基本事件;(2)等可能性:每个基本事件发生的机会是均等的。我们称这样的随机试验为古典概型。1、古典概型 古 典 概 型古典概型的 概率计算P(A)=事件A的概率是:记(1)所有基本事件的个数n(2)随机事件A包含的基本事件nAP(A)= 概 率 初 步例 题 分 析例2、掷一颗均匀的骰子,求掷得偶数点的概率。解:掷一颗均匀的骰子,全体基本事件是:
1, 2, 3, 4,5,6∴n=6 而掷得偶数点事件A={2, 4,6}∴nA=3∴P(A) =(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1)(5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) 例3:将一颗骰子先后抛掷2次,观察向上的点数,问:
(1) 共有多少种不同的结果?
(2) 两数之和是3的倍数的结果有多少种?
(3) 两数之和是3的倍数的概率是多少?关键:列出所有等可能事件,并找出满足条件的等可能事件。(6,6)例 题 分 析例3、同时掷两颗均匀的骰子,求掷得两颗骰子向上的点数之和是5的概率。解:掷两颗均匀的骰子,标记两颗骰子1号、2号便于区分。
每一颗骰子共有6种结果,两颗骰子同时抛共有6×6=36种结果 ∴n=36 而掷得向上的点数之和是5的事件
A={(1,4),(2, 3),( 3,2),(4,1)}∴m=4∴P(A) =训练二1、同时抛掷1角与1元的两枚硬币,计算:
(1)两枚硬币都出现正面的概率是
(2)一枚出现正面,一枚出现反面的概率是 0.250.52、在一次问题抢答的游戏,要求答题者在问题所列出的4个答案
中找出唯一正确答案。某抢答者不知道正确答案便随意说出
其中的一个答案,则这个答案恰好是正确答案的概率是 0.253、作投掷二颗骰子试验,用(x,y)表示结果,其中x表示第一
颗骰子出现的点数,y表示第二颗骰子出现的点数,求:
(1)求事件“出现点数之和大于8”的概率
(2)求事件“出现点数相等”的概率 古 典 概 型
1, 2, 3, 4,5,6∴n=6 而掷得偶数点事件A={2, 4,6}∴nA=3∴P(A) =(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1)(5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) 例3:将一颗骰子先后抛掷2次,观察向上的点数,问:
(1) 共有多少种不同的结果?
(2) 两数之和是3的倍数的结果有多少种?
(3) 两数之和是3的倍数的概率是多少?关键:列出所有等可能事件,并找出满足条件的等可能事件。(6,6)例 题 分 析例3、同时掷两颗均匀的骰子,求掷得两颗骰子向上的点数之和是5的概率。解:掷两颗均匀的骰子,标记两颗骰子1号、2号便于区分。
每一颗骰子共有6种结果,两颗骰子同时抛共有6×6=36种结果 ∴n=36 而掷得向上的点数之和是5的事件
A={(1,4),(2, 3),( 3,2),(4,1)}∴m=4∴P(A) =训练二1、同时抛掷1角与1元的两枚硬币,计算:
(1)两枚硬币都出现正面的概率是
(2)一枚出现正面,一枚出现反面的概率是 0.250.52、在一次问题抢答的游戏,要求答题者在问题所列出的4个答案
中找出唯一正确答案。某抢答者不知道正确答案便随意说出
其中的一个答案,则这个答案恰好是正确答案的概率是 0.253、作投掷二颗骰子试验,用(x,y)表示结果,其中x表示第一
颗骰子出现的点数,y表示第二颗骰子出现的点数,求:
(1)求事件“出现点数之和大于8”的概率
(2)求事件“出现点数相等”的概率 古 典 概 型
