2023年中考数学三轮冲刺复习:基础回练(1)(含解析)
文档属性
| 名称 | 2023年中考数学三轮冲刺复习:基础回练(1)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 522.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 16:07:27 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2023年中考数学三轮冲刺复习:基础回练(1)
一.选择题(共10小题)
1.下列实数中,最大的数是( )
A.π B. C.﹣2 D.3
2.2022年2月20日,北京冬奥会圆满闭幕,冬奥会的部分金牌榜如表所示,榜单上各国代表团获得的金牌数的众数为( )
代表团 挪威 德国 中国 美国 瑞典 荷兰 奥地利
金牌数 16 12 9 8 8 8 7
A.9 B.8.5 C.8 D.7
3.如图是某个几何体的三视图,则该几何体是( )
A.圆锥 B.长方体 C.三棱柱 D.圆柱
4.方程=的解为( )
A.x=1 B.x=﹣1 C.x=2 D.x=3
5.下列运算正确的是( )
A.a﹣2a=a B.(﹣a3b)2=a6b2
C.(a+b)2=a2+b2 D.
6.若A(﹣2,y1),B(1,y2),C(2,y3)三点均在反比例函数的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y1<y3<y2 D.y3<y1<y2
7.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数可能是( )
A.24 B.18 C.16 D.6
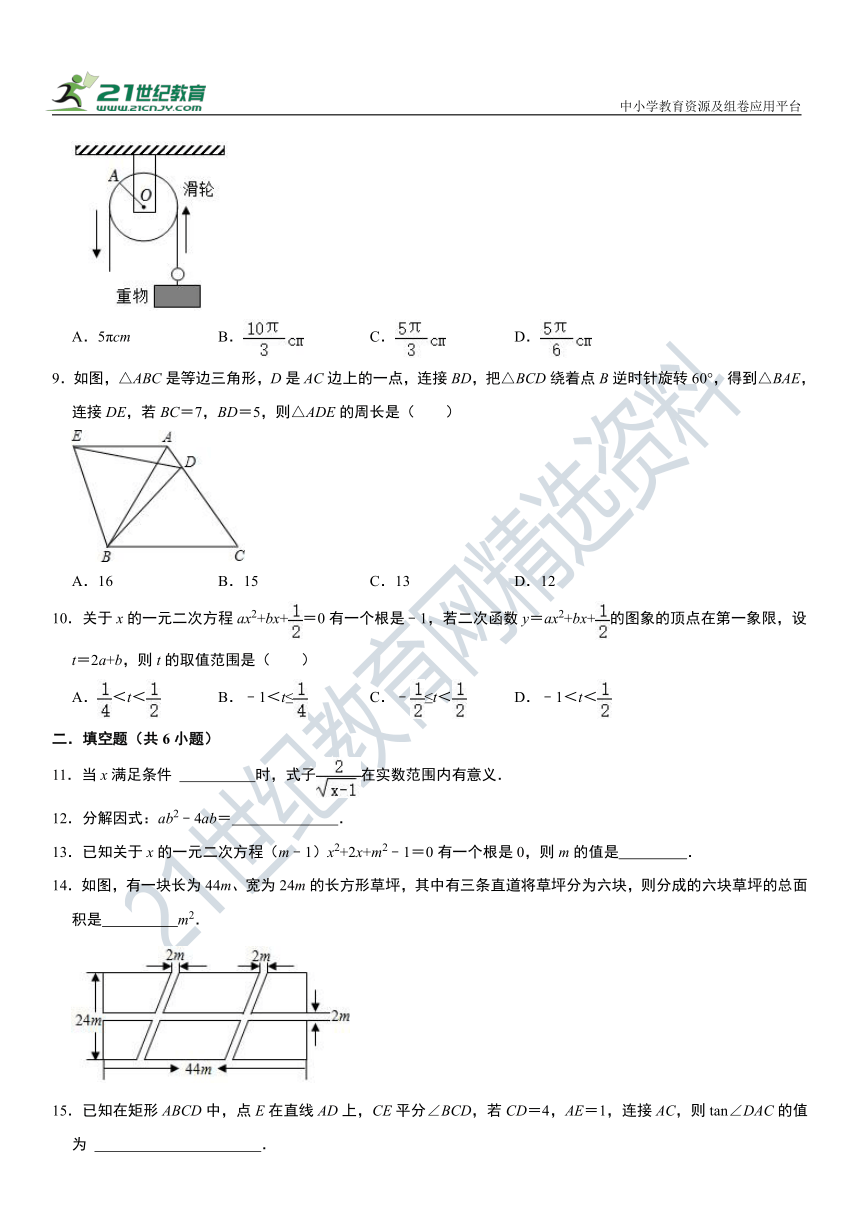
8.如图,若半径为2cm的定滑轮边缘上一点A绕中心O逆时针转动150°(绳索与滑轮之间没有滑动),则重物上升的高度为( )
A.5πcm B. C. D.
9.如图,△ABC是等边三角形,D是AC边上的一点,连接BD,把△BCD绕着点B逆时针旋转60°,得到△BAE,连接DE,若BC=7,BD=5,则△ADE的周长是( )
A.16 B.15 C.13 D.12
10.关于x的一元二次方程ax2+bx+=0有一个根是﹣1,若二次函数y=ax2+bx+的图象的顶点在第一象限,设t=2a+b,则t的取值范围是( )
A.<t< B.﹣1<t≤ C.﹣≤t< D.﹣1<t<
二.填空题(共6小题)
11.当x满足条件 时,式子在实数范围内有意义.
12.分解因式:ab2﹣4ab= .
13.已知关于x的一元二次方程(m﹣1)x2+2x+m2﹣1=0有一个根是0,则m的值是 .
14.如图,有一块长为44m、宽为24m的长方形草坪,其中有三条直道将草坪分为六块,则分成的六块草坪的总面积是 m2.
15.已知在矩形ABCD中,点E在直线AD上,CE平分∠BCD,若CD=4,AE=1,连接AC,则tan∠DAC的值为 .
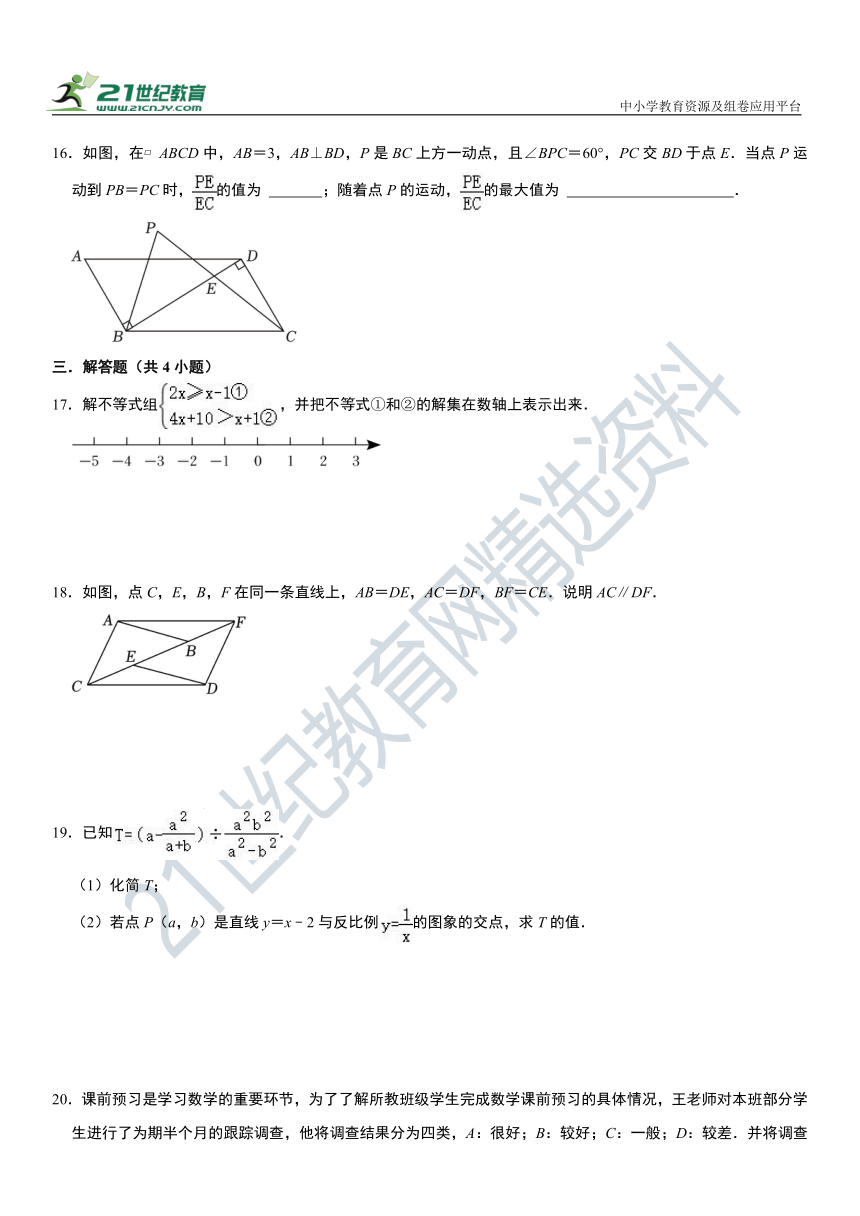
16.如图,在 ABCD中,AB=3,AB⊥BD,P是BC上方一动点,且∠BPC=60°,PC交BD于点E.当点P运动到PB=PC时,的值为 ;随着点P的运动,的最大值为 .
三.解答题(共4小题)
17.解不等式组,并把不等式①和②的解集在数轴上表示出来.
18.如图,点C,E,B,F在同一条直线上,AB=DE,AC=DF,BF=CE.说明AC∥DF.
19.已知.
(1)化简T;
(2)若点P(a,b)是直线y=x﹣2与反比例的图象的交点,求T的值.
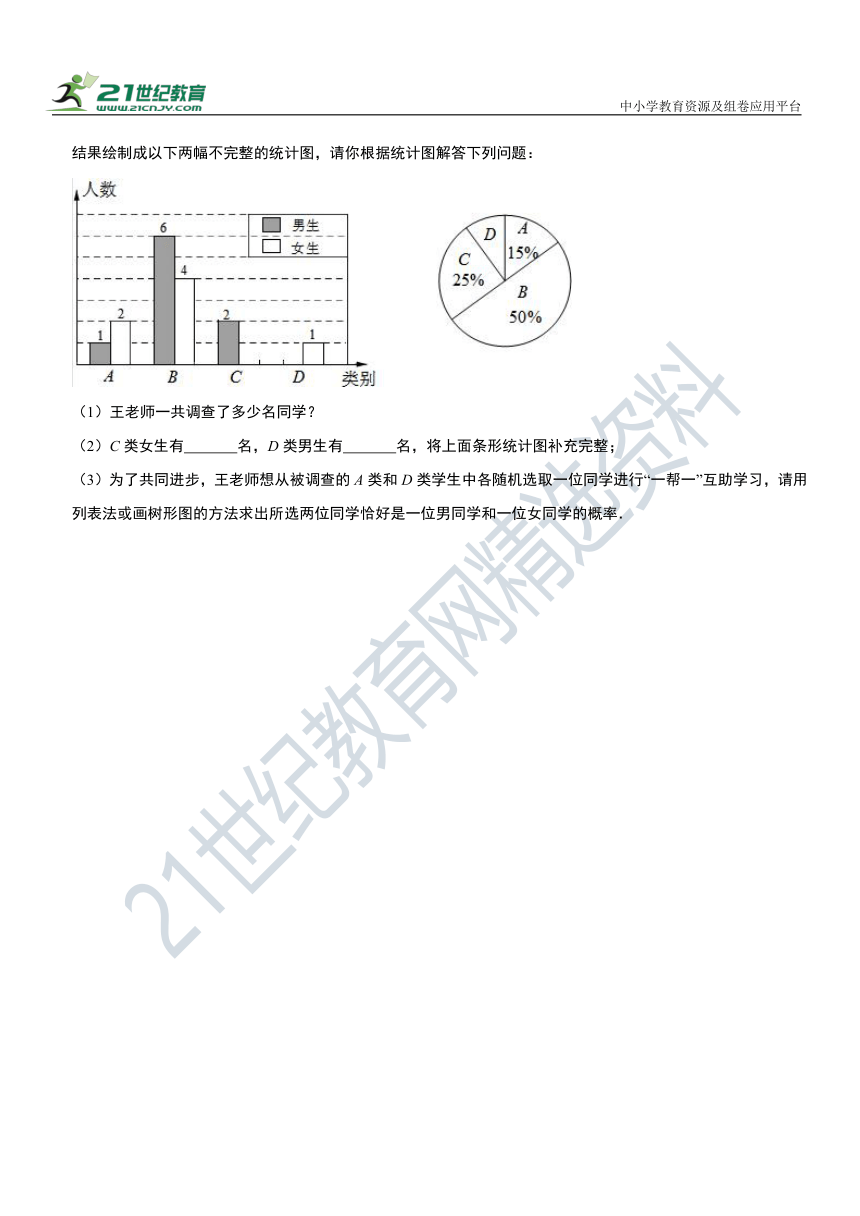
20.课前预习是学习数学的重要环节,为了了解所教班级学生完成数学课前预习的具体情况,王老师对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)王老师一共调查了多少名同学?
(2)C类女生有 名,D类男生有 名,将上面条形统计图补充完整;
(3)为了共同进步,王老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
2023年中考数学三轮冲刺复习:基础回练(1)
参考答案
一.选择题(共10小题)
1.下列实数中,最大的数是( )
A.π B. C.﹣2 D.3
【分析】根据实数的大小比较法则(正数大于0,0大于负数,正数大于一切负数,两个负数比大小,绝对值大的反而小)及无理数的估算进行分析求解.
【解答】解:∵π≈3.14,1<,
∴,
﹣2<<3<π,
故选:A.
2.2022年2月20日,北京冬奥会圆满闭幕,冬奥会的部分金牌榜如表所示,榜单上各国代表团获得的金牌数的众数为( )
代表团 挪威 德国 中国 美国 瑞典 荷兰 奥地利
金牌数 16 12 9 8 8 8 7
A.9 B.8.5 C.8 D.7
【分析】众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
【解答】解:数据8出现了3次,出现次数最多,
故这组数据的众数为8.
故选:C.
3.如图是某个几何体的三视图,则该几何体是( )
A.圆锥 B.长方体 C.三棱柱 D.圆柱
【分析】由主视图和左视图确定是柱体、锥体还是球体,再由俯视图确定具体形状.
【解答】解:根据主视图和左视图为矩形判断出是柱体,根据俯视图是圆可判断出这个几何体是圆柱.
故选:D.
4.方程=的解为( )
A.x=1 B.x=﹣1 C.x=2 D.x=3
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【解答】解:去分母得:2(4﹣x)=3(x+1),
去括号得:8﹣2x=3x+3,
解得:x=1,
检验:把x=1代入得:(x+1)(4﹣x)=2×3=6≠0,
则分式方程的解为x=1.
故选:A.
5.下列运算正确的是( )
A.a﹣2a=a B.(﹣a3b)2=a6b2
C.(a+b)2=a2+b2 D.
【分析】根据合并同类项法则、完全平方公式、幂的乘方运算法则、二次根式的乘法运算即可求出答案.
【解答】解:A、原式=﹣a,故A不符合题意.
B、原式=a6b2,故B符合题意.
C、原式=a2+2ab+b2,故C不符合题意.
D、原式=2,故D不符合题意.
故选:B.
6.若A(﹣2,y1),B(1,y2),C(2,y3)三点均在反比例函数的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y1<y3<y2 D.y3<y1<y2
【分析】先根据函数解析式中的比例系数k确定函数图象所在的象限,再根据各象限内点的坐标特点及函数的增减性解答.
【解答】解:∵反比例函数中,k<0,
∴此函数图象在二、四象限,
∵﹣2<0,
∴点A(﹣2,y1)在第二象限,
∴y1>0,
∵2>1>0,
∴B(1,y2),C(2,y3)两点在第四象限,
∴y2<0,y3<0,
∵函数图象在第四象限内为增函数,2>1,
∴y2<y3<0.
∴y1,y2,y3的大小关系为y2<y3<y1.
故选:B.
7.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数可能是( )
A.24 B.18 C.16 D.6
【分析】先由频率之和为1计算出白球的频率,再由数据总数×频率=频数计算白球的个数.
【解答】解:∵摸到红色球、黑色球的频率稳定在15%和45%,
∴摸到白球的频率为1﹣15%﹣45%=40%,
故口袋中白色球的个数可能是40×40%=16个.
故选:C.
8.如图,若半径为2cm的定滑轮边缘上一点A绕中心O逆时针转动150°(绳索与滑轮之间没有滑动),则重物上升的高度为( )
A.5πcm B. C. D.
【分析】根据定滑轮的性质得到重物上升的高度即为转过的弧长,利用弧长公式计算即可.
【解答】解:根据题意得:l==(cm),
则重物上升了cm,
故选:C.
9.如图,△ABC是等边三角形,D是AC边上的一点,连接BD,把△BCD绕着点B逆时针旋转60°,得到△BAE,连接DE,若BC=7,BD=5,则△ADE的周长是( )
A.16 B.15 C.13 D.12
【分析】根据旋转的性质得到△BDE是等边三角形得到DE=BD=5,由旋转的性质得到AE=CD,所以△AED的周长=AE+AD+DE=CD+AD+DE=AC+BD.
【解答】解:∵将△BCD绕点B逆时针旋转60°,得到△BAE,
∴BD=BE,∠DBE=60°,
∴△BDE是等边三角形,
∴DE=BD=5,
而△BCD绕点B逆时针旋转60°,得到△BAE,
∴AE=CD,
∴△AED的周长=AE+AD+DE=CD+AD+DE=AC+5=5+7=12.
故选:D.
10.关于x的一元二次方程ax2+bx+=0有一个根是﹣1,若二次函数y=ax2+bx+的图象的顶点在第一象限,设t=2a+b,则t的取值范围是( )
A.<t< B.﹣1<t≤ C.﹣≤t< D.﹣1<t<
【分析】二次函数的图象过点(﹣1,0),则a﹣b+=0,而t=2a+b=3a+,由二次函数的图象的顶点在第一象限,可得a<0,△=b2﹣4ac=a2++a﹣2a=(a﹣)2≥0,﹣>0,即可求解.
【解答】解:∵关于x的一元二次方程ax2+bx+=0有一个根是﹣1,
∴二次函数y=ax2+bx+的图象过点(﹣1,0),
∴a﹣b+=0,
∴b=a+,
而t=2a+b,
∴t=2a+a+=3a+,
∵二次函数y=ax2+bx+的图象的顶点在第一象限,
∴a<0,△=b2﹣4ac=a2++a﹣2a=(a﹣)2≥0,﹣>0,
∴b>0,
∴a+>0,
∴a>﹣,
∴﹣<a<0,
∴﹣1<3a+<,
∴﹣1<t<,
故选:D.
二.填空题(共6小题)
11.当x满足条件 x>1 时,式子在实数范围内有意义.
【分析】根据二次根式的被开方数是非负数,分式的分母不等于0即可得出答案.
【解答】解:∵x﹣1>0,
∴x>1.
故答案为:x>1.
12.分解因式:ab2﹣4ab= ab(b﹣4) .
【分析】直接提取公因式ab,进而得出答案.
【解答】解:ab2﹣4ab=ab(b﹣4).
故答案为:ab(b﹣4).
13.已知关于x的一元二次方程(m﹣1)x2+2x+m2﹣1=0有一个根是0,则m的值是 ﹣1 .
【分析】把x=0代入方程即可得到一个关于m的方程,即可求得m的值.
【解答】解:根据题意得:m2﹣1=0且m﹣1≠0
解得:m=﹣1
故答案是:﹣1.
14.如图,有一块长为44m、宽为24m的长方形草坪,其中有三条直道将草坪分为六块,则分成的六块草坪的总面积是 880 m2.
【分析】草坪的面积等于矩形的面积﹣三条路的面积+三条路重合部分的面积,由此计算即可.
【解答】解:S=44×24﹣2×24×2﹣2×44+2×2×2=880(m2).
故答案为:880.
15.已知在矩形ABCD中,点E在直线AD上,CE平分∠BCD,若CD=4,AE=1,连接AC,则tan∠DAC的值为 或 .
【分析】首先画出符合题意的图形,由于点E可以在边AD上也可以在边DA的延长线上,所以要分两种情况分别讨论求出tan∠DAC的值.
【解答】解:(1)当点E在边AD上时,如图1,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ECB=∠DEC,
∵CE平分∠BCD,
∴∠ECD=∠ECB,
∴∠DEC=∠DCE,
∴DE=CD=4,
∴AD=5,
∴tan∠DAC==;
(2)当点E在边DA的延长线上时,如图2,
由(1)可知DE=CD=4,
∴AD=DE﹣AE=3,
∴tan∠DAC==,
故答案为:或.
16.如图,在 ABCD中,AB=3,AB⊥BD,P是BC上方一动点,且∠BPC=60°,PC交BD于点E.当点P运动到PB=PC时,的值为 1 ;随着点P的运动,的最大值为 .
【分析】(1)根据三角函数值求∠ADB=30°,再根据PB=PC,∠BPC=60°推△BPC为等边三角形,根据三线合一性质求出最后比值;
(2)过点D作FC⊥BC交BD延长线于点F,过点P作PQ⊥BD交BD于点Q,根据∠BPC=∠BFC=60°证明点B、C、F、P四点共圆,再根据90°圆周角所对弦是直径得知BF为⊙O的直径,证△PQE∽△CDE推比例线段从而得知当PQ取最大值时,的值最大,最后利用三角函数求直径从而得到的最大值.
【解答】解:∵AB⊥BD,
∴∠ABD=90°,
∴sin∠ADB==,
∴∠ADB=30°,
在 ABCD中,AD∥BC,
∴∠DBC=∠ADB=30°,
∵PB=PC,∠BPC=60°,
∴△BPC为等边三角形,
∴∠PBC=60°,
∴∠PBD=30°=∠DBC,
∴PE=CE,
∴=1,
如图所示,过点D作FC⊥BC交BD延长线于点F,过点P作PQ⊥BD交BD于点Q,
∵FC⊥BC,
∴∠FCB=90°,
∵∠DBC=30°,
∴∠BFC=60°,
∵∠BPC=60°,
∴点B、C、F、P四点共圆,
∵∠FCB=90°,
∴BF为⊙O的直径,
∵AB∥CD,
∴∠BDC=∠ABD=90°,
∵PQ⊥BD,
∴∠PQD=90°,
∴∠PQD=∠CDQ,
∵∠PEQ=∠CED,
∴△PQE∽△CDE,
∴,
∴,
∴当PQ取最大值时,的值最大,
当点Q与点O重合时PQ最大,即PQ等于⊙O半径时,
在Rt△BFC中,sin∠BFC=,
∴BF=,
∴BC=4,
∴⊙O半径为2,
即PQ的最大值是2,
∴.
故答案为:1,.
三.解答题(共4小题)
17.解不等式组,并把不等式①和②的解集在数轴上表示出来.
【分析】按照解一元一次不等式组的步骤,进行计算即可解答.
【解答】解:,
解不等式①得:x≥﹣1,
解不等式②得:x>﹣3,
∴原不等式组的解集为:x≥﹣1,
该不等式组的解集在数轴上表示如图所示:
18.如图,点C,E,B,F在同一条直线上,AB=DE,AC=DF,BF=CE.说明AC∥DF.
【分析】先证明BC=EF,再根据SSS证明△ABC≌△DEF得到∠ACB=∠DFE,由此即可证明AC∥DF.
【解答】证明:∵CE=BF,
∴CE+BE=BF+BE,即BC=EF,
又∵AB=DE,AC=DF,
∴△ABC≌△DEF(SSS),
∴∠ACB=∠DFE,
∴AC∥DF.
19.已知.
(1)化简T;
(2)若点P(a,b)是直线y=x﹣2与反比例的图象的交点,求T的值.
【分析】(1)根据分式混合运算的法则把原式化简即可;
(2)由待定系数法可得出a﹣b=2,ab=1,代入T=即可求解.
【解答】解:(1)
=÷
=
=;
(2)∵点P(a,b)是直线y=x﹣2与反比例的图象的交点,
∴b=a﹣2,b=,
∴a﹣b=2,ab=1,
∴T===2.
20.课前预习是学习数学的重要环节,为了了解所教班级学生完成数学课前预习的具体情况,王老师对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)王老师一共调查了多少名同学?
(2)C类女生有 3 名,D类男生有 1 名,将上面条形统计图补充完整;
(3)为了共同进步,王老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
【分析】(1)根据B类有6+4=10人,所占的比例是50%,据此即可求得总人数;
(2)利用(1)中求得的总人数乘以对应的比例即可求得C类的人数,然后求得C类中女生人数,同理求得D类男生的人数;
(3)利用列举法即可表示出各种情况,然后利用概率公式即可求解.
【解答】解:(1)(6+4)÷50%=20.
所以王老师一共调查了20名学生.
(2)C类学生人数:20×25%=5(名)
C类女生人数:5﹣2=3(名),
D类学生占的百分比:1﹣15%﹣50%﹣25%=10%,
D类学生人数:20×10%=2(名),
D类男生人数:2﹣1=1(名),
故C类女生有3名,D类男生有1名;补充条形统计图
.
(3)由题意画树形图如下:
从树形图看出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选
两位同学恰好是一位男同学和一位女同学的结果共有3种.
所以P(所选两位同学恰好是一位男同学和一位女同学)==.
2023年中考数学三轮冲刺复习:基础回练(1)
一.选择题(共10小题)
1.下列实数中,最大的数是( )
A.π B. C.﹣2 D.3
2.2022年2月20日,北京冬奥会圆满闭幕,冬奥会的部分金牌榜如表所示,榜单上各国代表团获得的金牌数的众数为( )
代表团 挪威 德国 中国 美国 瑞典 荷兰 奥地利
金牌数 16 12 9 8 8 8 7
A.9 B.8.5 C.8 D.7
3.如图是某个几何体的三视图,则该几何体是( )
A.圆锥 B.长方体 C.三棱柱 D.圆柱
4.方程=的解为( )
A.x=1 B.x=﹣1 C.x=2 D.x=3
5.下列运算正确的是( )
A.a﹣2a=a B.(﹣a3b)2=a6b2
C.(a+b)2=a2+b2 D.
6.若A(﹣2,y1),B(1,y2),C(2,y3)三点均在反比例函数的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y1<y3<y2 D.y3<y1<y2
7.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数可能是( )
A.24 B.18 C.16 D.6
8.如图,若半径为2cm的定滑轮边缘上一点A绕中心O逆时针转动150°(绳索与滑轮之间没有滑动),则重物上升的高度为( )
A.5πcm B. C. D.
9.如图,△ABC是等边三角形,D是AC边上的一点,连接BD,把△BCD绕着点B逆时针旋转60°,得到△BAE,连接DE,若BC=7,BD=5,则△ADE的周长是( )
A.16 B.15 C.13 D.12
10.关于x的一元二次方程ax2+bx+=0有一个根是﹣1,若二次函数y=ax2+bx+的图象的顶点在第一象限,设t=2a+b,则t的取值范围是( )
A.<t< B.﹣1<t≤ C.﹣≤t< D.﹣1<t<
二.填空题(共6小题)
11.当x满足条件 时,式子在实数范围内有意义.
12.分解因式:ab2﹣4ab= .
13.已知关于x的一元二次方程(m﹣1)x2+2x+m2﹣1=0有一个根是0,则m的值是 .
14.如图,有一块长为44m、宽为24m的长方形草坪,其中有三条直道将草坪分为六块,则分成的六块草坪的总面积是 m2.
15.已知在矩形ABCD中,点E在直线AD上,CE平分∠BCD,若CD=4,AE=1,连接AC,则tan∠DAC的值为 .
16.如图,在 ABCD中,AB=3,AB⊥BD,P是BC上方一动点,且∠BPC=60°,PC交BD于点E.当点P运动到PB=PC时,的值为 ;随着点P的运动,的最大值为 .
三.解答题(共4小题)
17.解不等式组,并把不等式①和②的解集在数轴上表示出来.
18.如图,点C,E,B,F在同一条直线上,AB=DE,AC=DF,BF=CE.说明AC∥DF.
19.已知.
(1)化简T;
(2)若点P(a,b)是直线y=x﹣2与反比例的图象的交点,求T的值.
20.课前预习是学习数学的重要环节,为了了解所教班级学生完成数学课前预习的具体情况,王老师对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)王老师一共调查了多少名同学?
(2)C类女生有 名,D类男生有 名,将上面条形统计图补充完整;
(3)为了共同进步,王老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
2023年中考数学三轮冲刺复习:基础回练(1)
参考答案
一.选择题(共10小题)
1.下列实数中,最大的数是( )
A.π B. C.﹣2 D.3
【分析】根据实数的大小比较法则(正数大于0,0大于负数,正数大于一切负数,两个负数比大小,绝对值大的反而小)及无理数的估算进行分析求解.
【解答】解:∵π≈3.14,1<,
∴,
﹣2<<3<π,
故选:A.
2.2022年2月20日,北京冬奥会圆满闭幕,冬奥会的部分金牌榜如表所示,榜单上各国代表团获得的金牌数的众数为( )
代表团 挪威 德国 中国 美国 瑞典 荷兰 奥地利
金牌数 16 12 9 8 8 8 7
A.9 B.8.5 C.8 D.7
【分析】众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
【解答】解:数据8出现了3次,出现次数最多,
故这组数据的众数为8.
故选:C.
3.如图是某个几何体的三视图,则该几何体是( )
A.圆锥 B.长方体 C.三棱柱 D.圆柱
【分析】由主视图和左视图确定是柱体、锥体还是球体,再由俯视图确定具体形状.
【解答】解:根据主视图和左视图为矩形判断出是柱体,根据俯视图是圆可判断出这个几何体是圆柱.
故选:D.
4.方程=的解为( )
A.x=1 B.x=﹣1 C.x=2 D.x=3
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【解答】解:去分母得:2(4﹣x)=3(x+1),
去括号得:8﹣2x=3x+3,
解得:x=1,
检验:把x=1代入得:(x+1)(4﹣x)=2×3=6≠0,
则分式方程的解为x=1.
故选:A.
5.下列运算正确的是( )
A.a﹣2a=a B.(﹣a3b)2=a6b2
C.(a+b)2=a2+b2 D.
【分析】根据合并同类项法则、完全平方公式、幂的乘方运算法则、二次根式的乘法运算即可求出答案.
【解答】解:A、原式=﹣a,故A不符合题意.
B、原式=a6b2,故B符合题意.
C、原式=a2+2ab+b2,故C不符合题意.
D、原式=2,故D不符合题意.
故选:B.
6.若A(﹣2,y1),B(1,y2),C(2,y3)三点均在反比例函数的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y1<y3<y2 D.y3<y1<y2
【分析】先根据函数解析式中的比例系数k确定函数图象所在的象限,再根据各象限内点的坐标特点及函数的增减性解答.
【解答】解:∵反比例函数中,k<0,
∴此函数图象在二、四象限,
∵﹣2<0,
∴点A(﹣2,y1)在第二象限,
∴y1>0,
∵2>1>0,
∴B(1,y2),C(2,y3)两点在第四象限,
∴y2<0,y3<0,
∵函数图象在第四象限内为增函数,2>1,
∴y2<y3<0.
∴y1,y2,y3的大小关系为y2<y3<y1.
故选:B.
7.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数可能是( )
A.24 B.18 C.16 D.6
【分析】先由频率之和为1计算出白球的频率,再由数据总数×频率=频数计算白球的个数.
【解答】解:∵摸到红色球、黑色球的频率稳定在15%和45%,
∴摸到白球的频率为1﹣15%﹣45%=40%,
故口袋中白色球的个数可能是40×40%=16个.
故选:C.
8.如图,若半径为2cm的定滑轮边缘上一点A绕中心O逆时针转动150°(绳索与滑轮之间没有滑动),则重物上升的高度为( )
A.5πcm B. C. D.
【分析】根据定滑轮的性质得到重物上升的高度即为转过的弧长,利用弧长公式计算即可.
【解答】解:根据题意得:l==(cm),
则重物上升了cm,
故选:C.
9.如图,△ABC是等边三角形,D是AC边上的一点,连接BD,把△BCD绕着点B逆时针旋转60°,得到△BAE,连接DE,若BC=7,BD=5,则△ADE的周长是( )
A.16 B.15 C.13 D.12
【分析】根据旋转的性质得到△BDE是等边三角形得到DE=BD=5,由旋转的性质得到AE=CD,所以△AED的周长=AE+AD+DE=CD+AD+DE=AC+BD.
【解答】解:∵将△BCD绕点B逆时针旋转60°,得到△BAE,
∴BD=BE,∠DBE=60°,
∴△BDE是等边三角形,
∴DE=BD=5,
而△BCD绕点B逆时针旋转60°,得到△BAE,
∴AE=CD,
∴△AED的周长=AE+AD+DE=CD+AD+DE=AC+5=5+7=12.
故选:D.
10.关于x的一元二次方程ax2+bx+=0有一个根是﹣1,若二次函数y=ax2+bx+的图象的顶点在第一象限,设t=2a+b,则t的取值范围是( )
A.<t< B.﹣1<t≤ C.﹣≤t< D.﹣1<t<
【分析】二次函数的图象过点(﹣1,0),则a﹣b+=0,而t=2a+b=3a+,由二次函数的图象的顶点在第一象限,可得a<0,△=b2﹣4ac=a2++a﹣2a=(a﹣)2≥0,﹣>0,即可求解.
【解答】解:∵关于x的一元二次方程ax2+bx+=0有一个根是﹣1,
∴二次函数y=ax2+bx+的图象过点(﹣1,0),
∴a﹣b+=0,
∴b=a+,
而t=2a+b,
∴t=2a+a+=3a+,
∵二次函数y=ax2+bx+的图象的顶点在第一象限,
∴a<0,△=b2﹣4ac=a2++a﹣2a=(a﹣)2≥0,﹣>0,
∴b>0,
∴a+>0,
∴a>﹣,
∴﹣<a<0,
∴﹣1<3a+<,
∴﹣1<t<,
故选:D.
二.填空题(共6小题)
11.当x满足条件 x>1 时,式子在实数范围内有意义.
【分析】根据二次根式的被开方数是非负数,分式的分母不等于0即可得出答案.
【解答】解:∵x﹣1>0,
∴x>1.
故答案为:x>1.
12.分解因式:ab2﹣4ab= ab(b﹣4) .
【分析】直接提取公因式ab,进而得出答案.
【解答】解:ab2﹣4ab=ab(b﹣4).
故答案为:ab(b﹣4).
13.已知关于x的一元二次方程(m﹣1)x2+2x+m2﹣1=0有一个根是0,则m的值是 ﹣1 .
【分析】把x=0代入方程即可得到一个关于m的方程,即可求得m的值.
【解答】解:根据题意得:m2﹣1=0且m﹣1≠0
解得:m=﹣1
故答案是:﹣1.
14.如图,有一块长为44m、宽为24m的长方形草坪,其中有三条直道将草坪分为六块,则分成的六块草坪的总面积是 880 m2.
【分析】草坪的面积等于矩形的面积﹣三条路的面积+三条路重合部分的面积,由此计算即可.
【解答】解:S=44×24﹣2×24×2﹣2×44+2×2×2=880(m2).
故答案为:880.
15.已知在矩形ABCD中,点E在直线AD上,CE平分∠BCD,若CD=4,AE=1,连接AC,则tan∠DAC的值为 或 .
【分析】首先画出符合题意的图形,由于点E可以在边AD上也可以在边DA的延长线上,所以要分两种情况分别讨论求出tan∠DAC的值.
【解答】解:(1)当点E在边AD上时,如图1,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ECB=∠DEC,
∵CE平分∠BCD,
∴∠ECD=∠ECB,
∴∠DEC=∠DCE,
∴DE=CD=4,
∴AD=5,
∴tan∠DAC==;
(2)当点E在边DA的延长线上时,如图2,
由(1)可知DE=CD=4,
∴AD=DE﹣AE=3,
∴tan∠DAC==,
故答案为:或.
16.如图,在 ABCD中,AB=3,AB⊥BD,P是BC上方一动点,且∠BPC=60°,PC交BD于点E.当点P运动到PB=PC时,的值为 1 ;随着点P的运动,的最大值为 .
【分析】(1)根据三角函数值求∠ADB=30°,再根据PB=PC,∠BPC=60°推△BPC为等边三角形,根据三线合一性质求出最后比值;
(2)过点D作FC⊥BC交BD延长线于点F,过点P作PQ⊥BD交BD于点Q,根据∠BPC=∠BFC=60°证明点B、C、F、P四点共圆,再根据90°圆周角所对弦是直径得知BF为⊙O的直径,证△PQE∽△CDE推比例线段从而得知当PQ取最大值时,的值最大,最后利用三角函数求直径从而得到的最大值.
【解答】解:∵AB⊥BD,
∴∠ABD=90°,
∴sin∠ADB==,
∴∠ADB=30°,
在 ABCD中,AD∥BC,
∴∠DBC=∠ADB=30°,
∵PB=PC,∠BPC=60°,
∴△BPC为等边三角形,
∴∠PBC=60°,
∴∠PBD=30°=∠DBC,
∴PE=CE,
∴=1,
如图所示,过点D作FC⊥BC交BD延长线于点F,过点P作PQ⊥BD交BD于点Q,
∵FC⊥BC,
∴∠FCB=90°,
∵∠DBC=30°,
∴∠BFC=60°,
∵∠BPC=60°,
∴点B、C、F、P四点共圆,
∵∠FCB=90°,
∴BF为⊙O的直径,
∵AB∥CD,
∴∠BDC=∠ABD=90°,
∵PQ⊥BD,
∴∠PQD=90°,
∴∠PQD=∠CDQ,
∵∠PEQ=∠CED,
∴△PQE∽△CDE,
∴,
∴,
∴当PQ取最大值时,的值最大,
当点Q与点O重合时PQ最大,即PQ等于⊙O半径时,
在Rt△BFC中,sin∠BFC=,
∴BF=,
∴BC=4,
∴⊙O半径为2,
即PQ的最大值是2,
∴.
故答案为:1,.
三.解答题(共4小题)
17.解不等式组,并把不等式①和②的解集在数轴上表示出来.
【分析】按照解一元一次不等式组的步骤,进行计算即可解答.
【解答】解:,
解不等式①得:x≥﹣1,
解不等式②得:x>﹣3,
∴原不等式组的解集为:x≥﹣1,
该不等式组的解集在数轴上表示如图所示:
18.如图,点C,E,B,F在同一条直线上,AB=DE,AC=DF,BF=CE.说明AC∥DF.
【分析】先证明BC=EF,再根据SSS证明△ABC≌△DEF得到∠ACB=∠DFE,由此即可证明AC∥DF.
【解答】证明:∵CE=BF,
∴CE+BE=BF+BE,即BC=EF,
又∵AB=DE,AC=DF,
∴△ABC≌△DEF(SSS),
∴∠ACB=∠DFE,
∴AC∥DF.
19.已知.
(1)化简T;
(2)若点P(a,b)是直线y=x﹣2与反比例的图象的交点,求T的值.
【分析】(1)根据分式混合运算的法则把原式化简即可;
(2)由待定系数法可得出a﹣b=2,ab=1,代入T=即可求解.
【解答】解:(1)
=÷
=
=;
(2)∵点P(a,b)是直线y=x﹣2与反比例的图象的交点,
∴b=a﹣2,b=,
∴a﹣b=2,ab=1,
∴T===2.
20.课前预习是学习数学的重要环节,为了了解所教班级学生完成数学课前预习的具体情况,王老师对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)王老师一共调查了多少名同学?
(2)C类女生有 3 名,D类男生有 1 名,将上面条形统计图补充完整;
(3)为了共同进步,王老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
【分析】(1)根据B类有6+4=10人,所占的比例是50%,据此即可求得总人数;
(2)利用(1)中求得的总人数乘以对应的比例即可求得C类的人数,然后求得C类中女生人数,同理求得D类男生的人数;
(3)利用列举法即可表示出各种情况,然后利用概率公式即可求解.
【解答】解:(1)(6+4)÷50%=20.
所以王老师一共调查了20名学生.
(2)C类学生人数:20×25%=5(名)
C类女生人数:5﹣2=3(名),
D类学生占的百分比:1﹣15%﹣50%﹣25%=10%,
D类学生人数:20×10%=2(名),
D类男生人数:2﹣1=1(名),
故C类女生有3名,D类男生有1名;补充条形统计图
.
(3)由题意画树形图如下:
从树形图看出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选
两位同学恰好是一位男同学和一位女同学的结果共有3种.
所以P(所选两位同学恰好是一位男同学和一位女同学)==.
同课章节目录
