【核心素养目标】6.3三角形的中位线 教学设计
文档属性
| 名称 | 【核心素养目标】6.3三角形的中位线 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 1012.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-25 14:27:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
6.3三角形的中位线教学设计
课题 6.3三角形 单元 6 学科 数学 年级 八
教材分析 《三角形的中位线》是义务教育北师大版八年级(下)第六章《平行四边形》的第三节。教材安排一个学时完成。本节课主要研究三角形中位线定理及其应用。三角形中位线是三角形中重要的线段,三角形中位线定理是一个重要性质定理,它是前面已学过的平行线、全等三角形、平行四边形等知识内容的应用和深化,对进一步学习非常有用,尤其是在判定两直线平行和论证线段倍分关系时常常用到。
核心素养分析 在三角形中位线定理的证明及应用中,处处渗透了转化化归思想,它是一种重要的思想方法,无论在今后的学习还是在科学研究中都有着重要的作用,它对拓展学生的思维有着积极的意义,同时本节课培养学生的数形结合的思想,经历三角形中位线性质的探索过程,发展学生的动手操作能力,观察能力和抽象思维能力。
学习 目标 1.理解掌握三角形中位线的定义和性质。 2.经历三角形中位线性质的探索过程,发展学生的动手操作能力,观察能力和抽象思维能力。
重点 三角形中位线定理。
难点 证明三角形中位线性质定理时辅助线的添法和性质的灵活应用。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 如图,有一块三角形的蛋糕,准备平均分给四个小朋友,要求四人所分的形状和大小都相同,请设计合理的解决方案. 学生思考,解答问题。 通过问题,激发学生学习兴趣,激发学生求知欲和探索新知识的兴趣。
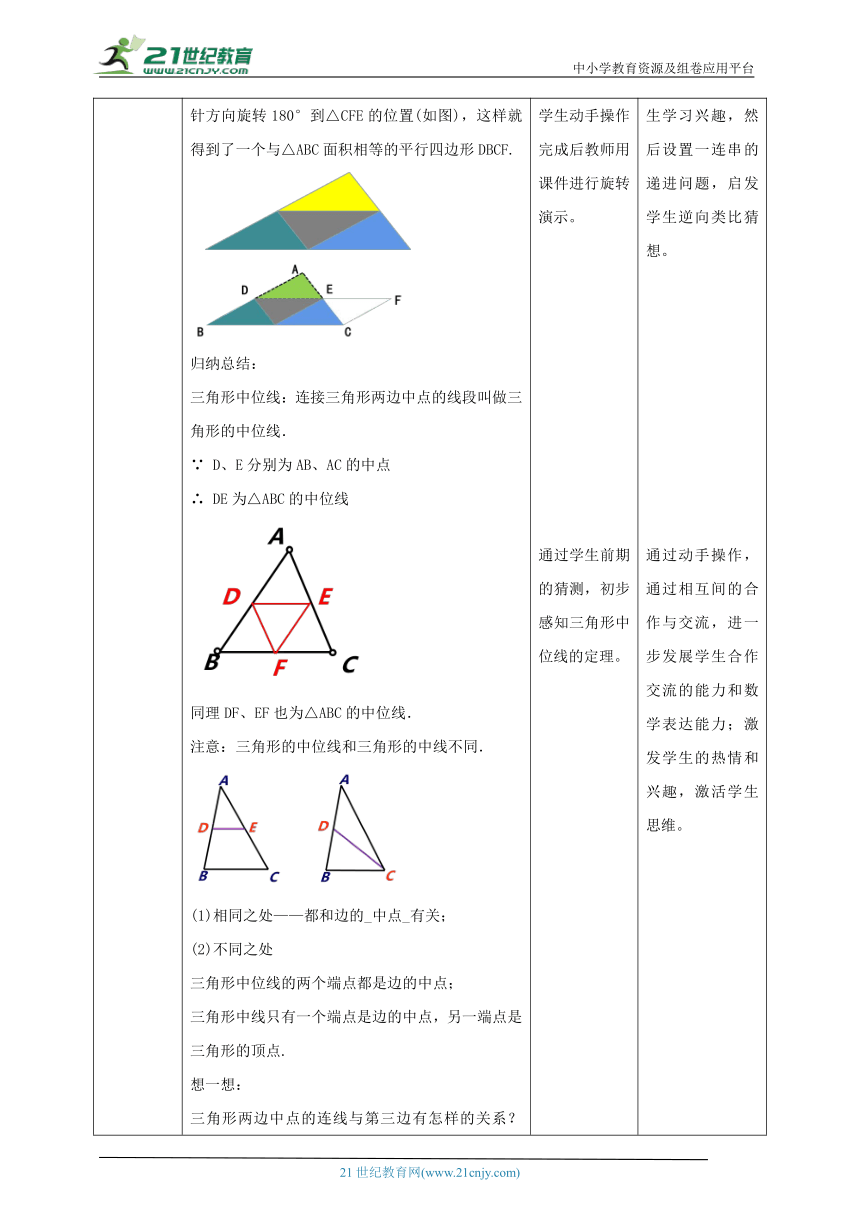
讲授新课 你能将任意一个三角形分成四个全等的三角形吗 你能通过剪拼的方式将一个三角形拼成一个与其面积相等的平行四边形吗? 如图,在△ABC中,连接每两边的中点,看上去就得到了四个全等的三角形,将△ADE绕点E按顺时针方向旋转180°到△CFE的位置(如图),这样就得到了一个与△ABC面积相等的平行四边形DBCF. 归纳总结: 三角形中位线:连接三角形两边中点的线段叫做三角形的中位线. ∵ D、E分别为AB、AC的中点 ∴ DE为△ABC的中位线 同理DF、EF也为△ABC的中位线. 注意:三角形的中位线和三角形的中线不同. (1)相同之处——都和边的_中点_有关; (2)不同之处 三角形中位线的两个端点都是边的中点; 三角形中线只有一个端点是边的中点,另一端点是三角形的顶点. 想一想: 三角形两边中点的连线与第三边有怎样的关系?能证明你的猜想吗? DE和边BC的关系 位置关系:平行 数量关系: DE是BC的一半 能说出理由吗 已知:在△ABC 中,DE是△ABC 的中位线 求证:DE∥BC,且DE=BC. 证明:如图,延长DE到F,使FE=DE,连接CF. 在△ADE和△CFE中, ∵AE=CE,∠1=∠2,DE=FE, ∴△ADE≌△CFE. ∴∠A=∠ECF,AD=CF. ∴CF∥AB. ∵BD=AD,∴ CF=BD. ∴四边形DBCF是平行四边形 ∴DF∥BC,DF=BC. ∴DE∥BC,DE=BC. 归纳总结: 三角形中位线定理: 三角形的中位线平行于第三边,并且等于第三边的一半. 用符号语言表示 ∵DE是△ABC的中位线 ∴DE∥BC,DE= 说明: (1)从条件看,以后我们看到中点,尤其是两个或者两个以上的中点时我们就要联想到三角形的中位线定理. (2)从结论看,它既可以得到线段的位置关系(平行),又可以得到线段的数量关系(倍分关系),大家以后在解决相关问题时要两方面结合起来灵活应用. 议一议 如图,任意画一个四边形,以四边形的中点为顶点组成一个新四边形,这个新四边形的形状有什么特征?请证明你的结论,并与同伴交流. 证明:如图,连接AC. ∵E、F、G、H分别是AB、BC、CD、DA的中点, ∴EF∥AC,EF=AC,HG∥AC,HG=AC. ∴EF∥HG,EF=HG. ∴四边形EFGH为平行四边形. 中点四边形的定义: 依次连接任意四边形各边中点所得到的四边形称为中点四边形. 拓展:不管四边形的形状怎样改变,中点四边形始终是平行四边形. (1)顺次连结平行四边形各边中点所得的四边形是_____ . (2)顺次连结矩形各边中点所得的四边形是___. (3)顺次连结菱形各边中点所得的四边形是___. (4)顺次连结正方形各边中点所得的四边形是_. (5)顺次连结梯形各边中点所得的四边形是__. (6)顺次连结等腰梯形各边中点所得的四边形是 . (7)顺次连结对角线相等的四边形各边中点所得的四边形是什么? (8)顺次连结对角线垂直的四边形各边中点所得的四边形是什么? (9)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么? 归纳总结: 实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否是特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关. 学生动手操作完成后教师用课件进行旋转演示。 通过学生前期的猜测,初步感知三角形中位线的定理。 学生猜想三角形中位线的性质并试着证明 归纳总结三角形中位线的性质 学生思考,教师进行补充证明,并进行拓展 通过一个有趣的动手操作问题入手,激发学生学习兴趣,然后设置一连串的递进问题,启发学生逆向类比猜想。 通过动手操作,通过相互间的合作与交流,进一步发展学生合作交流的能力和数学表达能力;激发学生的热情和兴趣,激活学生思维。 通过严密的几何证明将三角形中位线定理进行证明,由感性到理性,使学生经历定理的探究过程,积累数学活动的经验. 巩固三角形中位线定理,同时也兼顾平行四边形判定定理的熟练运用.
课堂练习 1、如图,在△ABC中,AB=3,BC=4,AC=2,D,E,F分别为AB,BC,AC的中点,连接DF,FE,则四边形DBEF的周长是( ) A.5 B.7 C.9 D.11 由三角形的三条中位线围成的三角形的周长是6,则这个三角形的周长是( ) A.6 B.8 C.10 D.12 3. 如图,顺次连接四边形ABCD四边的中点E,F,G,H,则四边形EFGH的形状一定是_____________. 4.在△ABC中,中线CE、BF相交点O、M、N分别是OB、OC的中点,则EF和MN的关系是_______________. 5.如图,D、E、F分别是△ABC三边的中点你能发现△DEF的面积与△ABC的面积有什么关系吗?为什么? 学生定时训练,自主解答,老师订正 通过各种形式的练习,进一步提高学生学习兴趣,使 学生的认知结构更加完善。同时强化本课的教学重点,突破教学难点。
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 训练学生总结归纳能 力;升华知识,拓展知识面,开阔思维。
板书 课题:6.3三角形的中位线 1、定义 2、性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.3三角形的中位线教学设计
课题 6.3三角形 单元 6 学科 数学 年级 八
教材分析 《三角形的中位线》是义务教育北师大版八年级(下)第六章《平行四边形》的第三节。教材安排一个学时完成。本节课主要研究三角形中位线定理及其应用。三角形中位线是三角形中重要的线段,三角形中位线定理是一个重要性质定理,它是前面已学过的平行线、全等三角形、平行四边形等知识内容的应用和深化,对进一步学习非常有用,尤其是在判定两直线平行和论证线段倍分关系时常常用到。
核心素养分析 在三角形中位线定理的证明及应用中,处处渗透了转化化归思想,它是一种重要的思想方法,无论在今后的学习还是在科学研究中都有着重要的作用,它对拓展学生的思维有着积极的意义,同时本节课培养学生的数形结合的思想,经历三角形中位线性质的探索过程,发展学生的动手操作能力,观察能力和抽象思维能力。
学习 目标 1.理解掌握三角形中位线的定义和性质。 2.经历三角形中位线性质的探索过程,发展学生的动手操作能力,观察能力和抽象思维能力。
重点 三角形中位线定理。
难点 证明三角形中位线性质定理时辅助线的添法和性质的灵活应用。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 如图,有一块三角形的蛋糕,准备平均分给四个小朋友,要求四人所分的形状和大小都相同,请设计合理的解决方案. 学生思考,解答问题。 通过问题,激发学生学习兴趣,激发学生求知欲和探索新知识的兴趣。
讲授新课 你能将任意一个三角形分成四个全等的三角形吗 你能通过剪拼的方式将一个三角形拼成一个与其面积相等的平行四边形吗? 如图,在△ABC中,连接每两边的中点,看上去就得到了四个全等的三角形,将△ADE绕点E按顺时针方向旋转180°到△CFE的位置(如图),这样就得到了一个与△ABC面积相等的平行四边形DBCF. 归纳总结: 三角形中位线:连接三角形两边中点的线段叫做三角形的中位线. ∵ D、E分别为AB、AC的中点 ∴ DE为△ABC的中位线 同理DF、EF也为△ABC的中位线. 注意:三角形的中位线和三角形的中线不同. (1)相同之处——都和边的_中点_有关; (2)不同之处 三角形中位线的两个端点都是边的中点; 三角形中线只有一个端点是边的中点,另一端点是三角形的顶点. 想一想: 三角形两边中点的连线与第三边有怎样的关系?能证明你的猜想吗? DE和边BC的关系 位置关系:平行 数量关系: DE是BC的一半 能说出理由吗 已知:在△ABC 中,DE是△ABC 的中位线 求证:DE∥BC,且DE=BC. 证明:如图,延长DE到F,使FE=DE,连接CF. 在△ADE和△CFE中, ∵AE=CE,∠1=∠2,DE=FE, ∴△ADE≌△CFE. ∴∠A=∠ECF,AD=CF. ∴CF∥AB. ∵BD=AD,∴ CF=BD. ∴四边形DBCF是平行四边形 ∴DF∥BC,DF=BC. ∴DE∥BC,DE=BC. 归纳总结: 三角形中位线定理: 三角形的中位线平行于第三边,并且等于第三边的一半. 用符号语言表示 ∵DE是△ABC的中位线 ∴DE∥BC,DE= 说明: (1)从条件看,以后我们看到中点,尤其是两个或者两个以上的中点时我们就要联想到三角形的中位线定理. (2)从结论看,它既可以得到线段的位置关系(平行),又可以得到线段的数量关系(倍分关系),大家以后在解决相关问题时要两方面结合起来灵活应用. 议一议 如图,任意画一个四边形,以四边形的中点为顶点组成一个新四边形,这个新四边形的形状有什么特征?请证明你的结论,并与同伴交流. 证明:如图,连接AC. ∵E、F、G、H分别是AB、BC、CD、DA的中点, ∴EF∥AC,EF=AC,HG∥AC,HG=AC. ∴EF∥HG,EF=HG. ∴四边形EFGH为平行四边形. 中点四边形的定义: 依次连接任意四边形各边中点所得到的四边形称为中点四边形. 拓展:不管四边形的形状怎样改变,中点四边形始终是平行四边形. (1)顺次连结平行四边形各边中点所得的四边形是_____ . (2)顺次连结矩形各边中点所得的四边形是___. (3)顺次连结菱形各边中点所得的四边形是___. (4)顺次连结正方形各边中点所得的四边形是_. (5)顺次连结梯形各边中点所得的四边形是__. (6)顺次连结等腰梯形各边中点所得的四边形是 . (7)顺次连结对角线相等的四边形各边中点所得的四边形是什么? (8)顺次连结对角线垂直的四边形各边中点所得的四边形是什么? (9)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么? 归纳总结: 实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否是特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关. 学生动手操作完成后教师用课件进行旋转演示。 通过学生前期的猜测,初步感知三角形中位线的定理。 学生猜想三角形中位线的性质并试着证明 归纳总结三角形中位线的性质 学生思考,教师进行补充证明,并进行拓展 通过一个有趣的动手操作问题入手,激发学生学习兴趣,然后设置一连串的递进问题,启发学生逆向类比猜想。 通过动手操作,通过相互间的合作与交流,进一步发展学生合作交流的能力和数学表达能力;激发学生的热情和兴趣,激活学生思维。 通过严密的几何证明将三角形中位线定理进行证明,由感性到理性,使学生经历定理的探究过程,积累数学活动的经验. 巩固三角形中位线定理,同时也兼顾平行四边形判定定理的熟练运用.
课堂练习 1、如图,在△ABC中,AB=3,BC=4,AC=2,D,E,F分别为AB,BC,AC的中点,连接DF,FE,则四边形DBEF的周长是( ) A.5 B.7 C.9 D.11 由三角形的三条中位线围成的三角形的周长是6,则这个三角形的周长是( ) A.6 B.8 C.10 D.12 3. 如图,顺次连接四边形ABCD四边的中点E,F,G,H,则四边形EFGH的形状一定是_____________. 4.在△ABC中,中线CE、BF相交点O、M、N分别是OB、OC的中点,则EF和MN的关系是_______________. 5.如图,D、E、F分别是△ABC三边的中点你能发现△DEF的面积与△ABC的面积有什么关系吗?为什么? 学生定时训练,自主解答,老师订正 通过各种形式的练习,进一步提高学生学习兴趣,使 学生的认知结构更加完善。同时强化本课的教学重点,突破教学难点。
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 训练学生总结归纳能 力;升华知识,拓展知识面,开阔思维。
板书 课题:6.3三角形的中位线 1、定义 2、性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
