【教师整理】高中物理(人教版)必修一:第二章 第一节 实验:探究小车速度随时间变化的规律(共34张PPT)
文档属性
| 名称 | 【教师整理】高中物理(人教版)必修一:第二章 第一节 实验:探究小车速度随时间变化的规律(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 143.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2014-08-13 17:23:35 | ||
图片预览










文档简介
课件34张PPT。第二章第一节 实验:探究小车速度随时间
变化的规律
课前导航
知识精析
一、实验步骤
1.把附有滑轮的长木板放在实验桌上,把打点计时器固定在长木板上不带滑轮的一侧,将细绳绕过滑轮,下端挂适当的钩码,将纸带连在小车后面,并穿过打点计时器.
2.将小车停在靠近打点计时器的位置,启动打点计时器,释放纸带,打点计时器在纸带上打下一行小点,然后关闭电源,取下纸带.
3.换上纸带重复操作两次.
4.在三条纸带中选择一条最清晰的,舍弃开头一些过于密集的点,找一个适当点作为计时起点.
5.选择相隔0.1 s的若干计数点进行测量,把数据填入设计好的表格.
6.增减所挂钩码数,再做两次实验.
二、数据分析
1.根据实验记录数据,计算出各计数点瞬时速度,填入表中.
2.以速度v为纵轴,时间t为横轴,建立直角坐标系,根据表中数据描点,将这些点连成一条直线.连线时应使尽量多的点落在直线上,不在直线上的点要尽量对称分布在直线两侧.误差较大的点可舍去.
3.分析v-t图象,描述出小车运动速度随时间变化的规律.
三、注意事项
1.开始释放小车时,应使小车靠近打点计时器.
2.先接通电源,等打点稳定后,再释放小车.
3.取下纸带前,先断开电源.
5.要防止钩码落地,避免小车跟滑轮相碰,当小车到达滑轮前及时用手按住.
6.要区分打点计时器打出的计时点和人为选取的计数点,一般在纸带上每隔4个点取一个计数点,即时间间隔T=0.02×5 s=0.1 s.
7.在坐标纸上画v-t图象时,注意坐标轴单位长度的选取,使图象分布在坐标平面的大部分面积.
四、误差分析
1.根据纸带测量的位移有误差.
2.根据位移计算的瞬时速度有误差.
3.木板的粗糙程度并非完全相同.
方法指导
一、根据纸带判断物体速度随时间变化的规律
例1 在“探究小车速度随时间变化的规律”的实验中,图7-2甲给出了从0点开始,每5个点取一个计数点的纸带,其中0,1,2,3,4,5,6都为计数点.测得:x1=1.40 cm,x2=1.90 cm,x3=2.38 cm,x4=2.88 cm,x5=3.39 cm,x6=3.87 cm.那么:
图7-2甲
(1)在计时器打出点1,2,3,4,5时,小车的速度分别为:
v1=16.50 cm/s,v2=________cm/s,v3=26.30 cm/s,v4=31.35 cm/s,v5=________cm/s.
(2)在平面直角坐标系中作出v-t图象.
(3)分析小车运动速度随时间变化的规律.
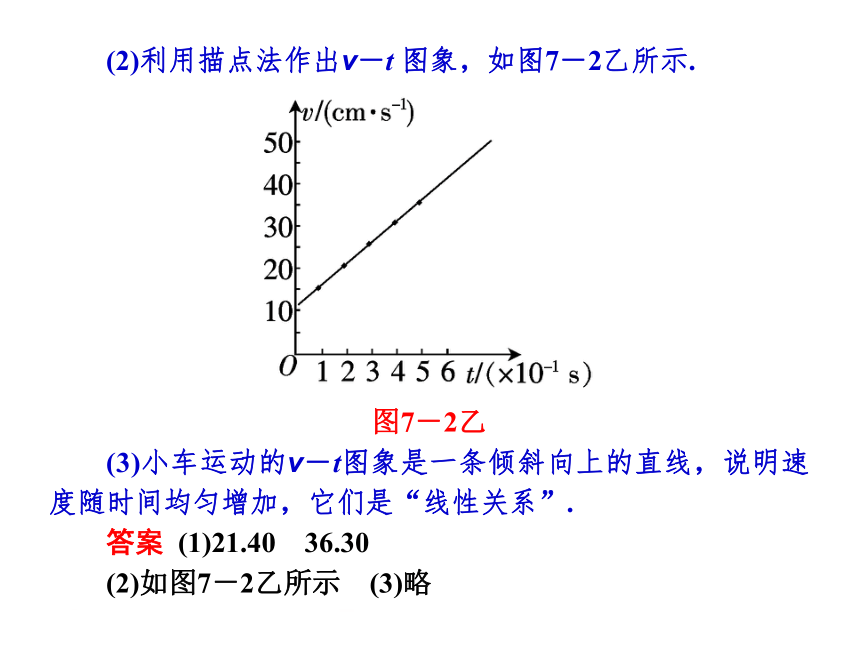
(2)利用描点法作出v-t 图象,如图7-2乙所示.
图7-2乙
(3)小车运动的v-t图象是一条倾斜向上的直线,说明速度随时间均匀增加,它们是“线性关系”.
答案 (1)21.40 36.30
(2)如图7-2乙所示 (3)略
二、根据纸带求匀变速直线运动的加速度
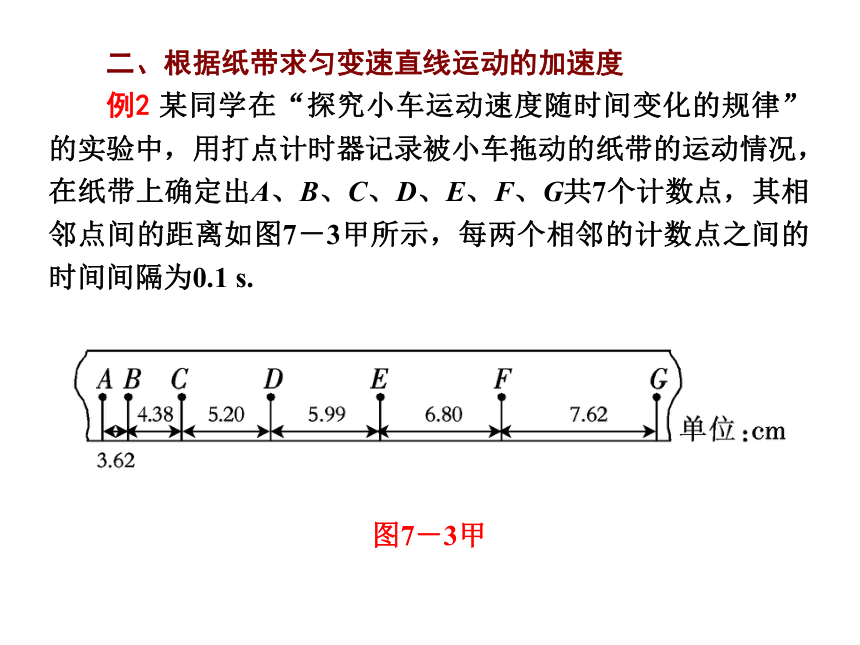
例2 某同学在“探究小车运动速度随时间变化的规律”的实验中,用打点计时器记录被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点,其相邻点间的距离如图7-3甲所示,每两个相邻的计数点之间的时间间隔为0.1 s.
图7-3甲 (1)若从纸带上打A点的时刻开始计时,将B、C、D、E、F各个时刻的瞬时速度标在如图7-3乙所示的坐标纸上,并画出小车的瞬时速度随时间变化的关系图线.
图7-3乙
(2)计算加速度的大小是多少?
根据计算得出的速度及其对应的时刻,得到如图7-3丙所示的5个圆点,用描点法作出的小车瞬时速度随时间变化的关系图线如图7-3 丙所示.
图7-3丙
互动平台
育才老师和细心同学关于位移图象和速度图象的对话
细心:有些位移图象和速度图象看起来十分相似,但表示的意义截然不同.
育才:对.例如图7-4中的甲、乙两图,一个是位移图象,一个是速度图象,差别就在于它们的纵轴表示的物理意义不同,你能简单地说一下两图分别代表什么运动吗?
图7-4 细心:甲图表示的是物体先向前匀速直线运动,接着倒回来匀速运动,回到原出发点,然后又向前和返回,直到再次回到出发点.乙图表示的是物体先向前匀加速直线运动,接着向前匀减速直线运动,然后再向前做匀加速和匀减速运动,而物体是始终朝前走.
育才:看来你对这些运动图象掌握得非常好.
课时8 匀变速直线运动的速度与
时间的关系
课前导航
轮船为什么总是逆水靠岸?
如果你乘坐轮船,就会发现一个很有趣的现象:每当轮船要靠岸的时候,总是要把船头顶着流水,慢慢地驶向码头,然后平稳靠岸.在长江或其他大河里顺流而下的船只,当它们到岸时,不会立刻靠岸,都要掉头,使船变成逆着水流方向行驶以后,才缓缓靠岸.实际上这是利用了流水对船身的阻力,起到了使船“刹车”的作用.
请你思考:
1.在船逆水靠岸停下的过程中,船的加速度方向与船的速度方向相同还是相反?如果以船速为正方向,船的加速度是正还是负?
2.假设船停下的过程中,加速度大小恒为a,船速由v减到零,船逆水航行的距离应为多长? 基础梳理
知识精析
一、匀变速直线运动的速度公式
1.注意弄清公式中各符号的意义:
(1)v0、v分别表示物体的初、末速度.
(2)a为时间t范围内的加速度,且a为恒量.
2.公式v=v0+at是个矢量式:
(1)一般规定v0的方向为正方向,a与v0同向时表明物体的速度随时间均匀增加,a与v0反向时,表明物体的速度随时间均匀减小.
(2)应用公式v=v0+at进行计算时,除“+”外,其他各量要根据正方向的规定情况加上相应的“正负”号.
3.几种特殊的匀变速直线运动:
(1)当a=0时,公式为v=v0.
(2)当v0=0时,公式为v=at.
(3)当a<0时,公式为v=v0-at(此时a取绝对值). 二、识别v-t图象
如图8-1所示,v-t图象描述速度随时间的变化关系,记录了任意时刻物体的速度,用图象法处理物理问题的优点是:形象直观、清晰便捷,能清楚地反映运动物体的速度随时间变化的情况,便于从整体上认识运动的过程、运动的特点.
图8-1
1.两图线的交点:表示该时刻两物体速度相同.
2.图线与坐标轴的交点:
(1)与t轴的交点:表示速度为零,方向改变.
(2)与v轴的交点:表示初速度.
3.图线的拐点(折点):
表示加速度改变,速度出现极值.
4.几个常见弯曲图线:(图线的斜率表示物体的加速度)
方法指导
一、速度时间关系式的应用
例1 某汽车在某路面紧急刹车时,加速度的大小是6 m/s2,如果必须在2.5 s内停下来,则该汽车的行驶速度最大不能超过多少?(假设汽车刹车后做匀减速运动)
解析 我们研究的是汽车从开始刹车到停止运动这个过程.在这个过程中,汽车做匀减速运动,加速度的大小是6 m/s2.由于是减速运动,加速度的方向与速度方向相反,如果设汽车运动的方向为正,则汽车的加速度方向为负,我们把它记为a=-6 m/s2.这个过程的末速度v是零,初速度就是我们所求的允许最高速度,记为v0,过程的持续时间t=2.5 s. 解法一 根据v=v0+at,有v0=v-at=0-(-6 m/s2)×2.5 s=15 m/s=54 km/h,汽车的速度不能超过54 km/h.
解法二 反过来汽车可以看做是初速度为零的匀加速运动.则v=at=6×2.5=15 m/s=54km/h.
答案 不能超过54 km/h
点评 根据匀加速直线运动的速度公式即可得出答案.不过要注意加速度是负值.匀减速到零的直线运动可以反过来看做是初速度为零的匀加速直线运动,这样解起来很方便.车最终停下来,所以末速度为零,这一点容易忽略,导致缺少条件,解不出答案.
变式训练1
汽车以40 km/h的速度匀速行驶,
(1)若汽车以0.6 m/s2的加速度加速,则10 s后速度能达到多少?
(2)若汽车刹车以0.6 m/s2的加速度减速,则10 s 后速度减为多少?
(3)若汽车刹车以3 m/s2的加速度减速,则10 s后速度为多少?
解析 汽车做匀加速运动时,可直接应用公式v=v0+at,求10 s后的速度,汽车做匀减速运动时,要先验证减速为零时所用时间与10 s的关系,若大于10 s,则直接应用公式v=v0+at,若小于10 s,则10 s后的速度为零.
二、利用v-t图象分析物体的运动
例2 分析如图8-2所示的图线,物体在各段时间内做何种运动?哪一时间内的加速度最大?
图8-2
解析 v-t图象的斜率等于加速度的大小,负斜率表示加速度方向与规定的正方向相反.
由v-t图象的意义可知,物体在0~t1、t4~t5时间内做匀加速运动;t2~t3、t6~t7时间内做匀减速直线运动;在t1~t2、t5~t6时间内做匀速直线运动. v-t图象的斜率大小等于加速度大小,t2~t3段斜率最大,所以加速度最大.
答案 略
点评 速度大小的变化情况仅由速度和加速度方向的关系确定,不要认为加速度为负值,就做匀减速运动,如在本题中t4~t5时间内,虽然加速度为负值,但速度也为负值,即两者方向相同,物体做匀加速直线运动. 变式训练2
某质点的运动图象如图8-3所示,则质点( )
图8-3
A.在第1 s末运动方向发生变化
B.在第2 s末运动方向发生变化
C.在第2 s内速度越来越大
D.在第3 s内速度越来越大 解析 题图为v-t图象,由图可知,第1 s末速度达到最大,运动方向不变,选项A错误;第2 s末速度为零,然后反向加速,速度方向改变,选项B正确;第2 s内质点做减速运动,速度减小,选项C错误;第3 s内质点做反向的加速运动,速度增大,选项D正确.
答案 BD 三、物体分阶段运动问题
例3 发射卫星一般采用多级火箭,第一级火箭点火后,使卫星向上做匀加速运动的加速度为50 m/s2,燃烧30 s后第一级脱离,第二级火箭没有马上点火,所以卫星向上做加速度为10 m/s2的匀减速运动,10 s后第二级火箭启动,卫星的加速度为80 m/s2,这样经过1分半钟等第二级火箭脱离时,卫星的线速度为多大? 解析 整个过程中卫星的运动不是匀变速直线运动,但可以分解为三个匀变速直线运动处理.
第一级火箭燃烧完毕时的速度为:
v1=a1t1=1500 m/s
减速上升10 s后的速度为:
v2=v1-a2t2=1400 m/s
第二级火箭熄火时的速度为:
v3=v2+a3t3=8600 m/s.
答案 8600 m/s
点评 对于过程复杂的运动,我们可以将其分为几个简单运动,然后在每段运动中运用公式解答,从而达到化繁为简的目的. 变式训练3
升降机由静止开始以加速度a1匀加速上升2 s后速度达到3 m/s,接着匀速运动了一段时间,最后再以大小为1 m/s2的加速度匀减速上升才停下来.求:
(1)升降机匀加速上升的加速度a1.
(2)升降机匀减速上升的时间t2.
解析 设升降机向上运动的方向为正方向.
(1)匀加速上升过程,初速度v0=0,末速度v1=3 m/s,t1=2 s.根据vt=v0+at,得
答案 (1)1.5 m/s2 (2)3 s 互动平台
育才老师、粗心和细心同学关于匀减速运动规律的理解的对话
育才:汽车以36 km/h的速度行驶,刹车得到的加速度大小为4 m/s2,从刹车开始计时,前3 s内汽车通过的距离是多少?
粗心:应用位移公式不就迎刃而解了吗? 育才:3 s末的速度怎样了?
变化的规律
课前导航
知识精析
一、实验步骤
1.把附有滑轮的长木板放在实验桌上,把打点计时器固定在长木板上不带滑轮的一侧,将细绳绕过滑轮,下端挂适当的钩码,将纸带连在小车后面,并穿过打点计时器.
2.将小车停在靠近打点计时器的位置,启动打点计时器,释放纸带,打点计时器在纸带上打下一行小点,然后关闭电源,取下纸带.
3.换上纸带重复操作两次.
4.在三条纸带中选择一条最清晰的,舍弃开头一些过于密集的点,找一个适当点作为计时起点.
5.选择相隔0.1 s的若干计数点进行测量,把数据填入设计好的表格.
6.增减所挂钩码数,再做两次实验.
二、数据分析
1.根据实验记录数据,计算出各计数点瞬时速度,填入表中.
2.以速度v为纵轴,时间t为横轴,建立直角坐标系,根据表中数据描点,将这些点连成一条直线.连线时应使尽量多的点落在直线上,不在直线上的点要尽量对称分布在直线两侧.误差较大的点可舍去.
3.分析v-t图象,描述出小车运动速度随时间变化的规律.
三、注意事项
1.开始释放小车时,应使小车靠近打点计时器.
2.先接通电源,等打点稳定后,再释放小车.
3.取下纸带前,先断开电源.
5.要防止钩码落地,避免小车跟滑轮相碰,当小车到达滑轮前及时用手按住.
6.要区分打点计时器打出的计时点和人为选取的计数点,一般在纸带上每隔4个点取一个计数点,即时间间隔T=0.02×5 s=0.1 s.
7.在坐标纸上画v-t图象时,注意坐标轴单位长度的选取,使图象分布在坐标平面的大部分面积.
四、误差分析
1.根据纸带测量的位移有误差.
2.根据位移计算的瞬时速度有误差.
3.木板的粗糙程度并非完全相同.
方法指导
一、根据纸带判断物体速度随时间变化的规律
例1 在“探究小车速度随时间变化的规律”的实验中,图7-2甲给出了从0点开始,每5个点取一个计数点的纸带,其中0,1,2,3,4,5,6都为计数点.测得:x1=1.40 cm,x2=1.90 cm,x3=2.38 cm,x4=2.88 cm,x5=3.39 cm,x6=3.87 cm.那么:
图7-2甲
(1)在计时器打出点1,2,3,4,5时,小车的速度分别为:
v1=16.50 cm/s,v2=________cm/s,v3=26.30 cm/s,v4=31.35 cm/s,v5=________cm/s.
(2)在平面直角坐标系中作出v-t图象.
(3)分析小车运动速度随时间变化的规律.
(2)利用描点法作出v-t 图象,如图7-2乙所示.
图7-2乙
(3)小车运动的v-t图象是一条倾斜向上的直线,说明速度随时间均匀增加,它们是“线性关系”.
答案 (1)21.40 36.30
(2)如图7-2乙所示 (3)略
二、根据纸带求匀变速直线运动的加速度
例2 某同学在“探究小车运动速度随时间变化的规律”的实验中,用打点计时器记录被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点,其相邻点间的距离如图7-3甲所示,每两个相邻的计数点之间的时间间隔为0.1 s.
图7-3甲 (1)若从纸带上打A点的时刻开始计时,将B、C、D、E、F各个时刻的瞬时速度标在如图7-3乙所示的坐标纸上,并画出小车的瞬时速度随时间变化的关系图线.
图7-3乙
(2)计算加速度的大小是多少?
根据计算得出的速度及其对应的时刻,得到如图7-3丙所示的5个圆点,用描点法作出的小车瞬时速度随时间变化的关系图线如图7-3 丙所示.
图7-3丙
互动平台
育才老师和细心同学关于位移图象和速度图象的对话
细心:有些位移图象和速度图象看起来十分相似,但表示的意义截然不同.
育才:对.例如图7-4中的甲、乙两图,一个是位移图象,一个是速度图象,差别就在于它们的纵轴表示的物理意义不同,你能简单地说一下两图分别代表什么运动吗?
图7-4 细心:甲图表示的是物体先向前匀速直线运动,接着倒回来匀速运动,回到原出发点,然后又向前和返回,直到再次回到出发点.乙图表示的是物体先向前匀加速直线运动,接着向前匀减速直线运动,然后再向前做匀加速和匀减速运动,而物体是始终朝前走.
育才:看来你对这些运动图象掌握得非常好.
课时8 匀变速直线运动的速度与
时间的关系
课前导航
轮船为什么总是逆水靠岸?
如果你乘坐轮船,就会发现一个很有趣的现象:每当轮船要靠岸的时候,总是要把船头顶着流水,慢慢地驶向码头,然后平稳靠岸.在长江或其他大河里顺流而下的船只,当它们到岸时,不会立刻靠岸,都要掉头,使船变成逆着水流方向行驶以后,才缓缓靠岸.实际上这是利用了流水对船身的阻力,起到了使船“刹车”的作用.
请你思考:
1.在船逆水靠岸停下的过程中,船的加速度方向与船的速度方向相同还是相反?如果以船速为正方向,船的加速度是正还是负?
2.假设船停下的过程中,加速度大小恒为a,船速由v减到零,船逆水航行的距离应为多长? 基础梳理
知识精析
一、匀变速直线运动的速度公式
1.注意弄清公式中各符号的意义:
(1)v0、v分别表示物体的初、末速度.
(2)a为时间t范围内的加速度,且a为恒量.
2.公式v=v0+at是个矢量式:
(1)一般规定v0的方向为正方向,a与v0同向时表明物体的速度随时间均匀增加,a与v0反向时,表明物体的速度随时间均匀减小.
(2)应用公式v=v0+at进行计算时,除“+”外,其他各量要根据正方向的规定情况加上相应的“正负”号.
3.几种特殊的匀变速直线运动:
(1)当a=0时,公式为v=v0.
(2)当v0=0时,公式为v=at.
(3)当a<0时,公式为v=v0-at(此时a取绝对值). 二、识别v-t图象
如图8-1所示,v-t图象描述速度随时间的变化关系,记录了任意时刻物体的速度,用图象法处理物理问题的优点是:形象直观、清晰便捷,能清楚地反映运动物体的速度随时间变化的情况,便于从整体上认识运动的过程、运动的特点.
图8-1
1.两图线的交点:表示该时刻两物体速度相同.
2.图线与坐标轴的交点:
(1)与t轴的交点:表示速度为零,方向改变.
(2)与v轴的交点:表示初速度.
3.图线的拐点(折点):
表示加速度改变,速度出现极值.
4.几个常见弯曲图线:(图线的斜率表示物体的加速度)
方法指导
一、速度时间关系式的应用
例1 某汽车在某路面紧急刹车时,加速度的大小是6 m/s2,如果必须在2.5 s内停下来,则该汽车的行驶速度最大不能超过多少?(假设汽车刹车后做匀减速运动)
解析 我们研究的是汽车从开始刹车到停止运动这个过程.在这个过程中,汽车做匀减速运动,加速度的大小是6 m/s2.由于是减速运动,加速度的方向与速度方向相反,如果设汽车运动的方向为正,则汽车的加速度方向为负,我们把它记为a=-6 m/s2.这个过程的末速度v是零,初速度就是我们所求的允许最高速度,记为v0,过程的持续时间t=2.5 s. 解法一 根据v=v0+at,有v0=v-at=0-(-6 m/s2)×2.5 s=15 m/s=54 km/h,汽车的速度不能超过54 km/h.
解法二 反过来汽车可以看做是初速度为零的匀加速运动.则v=at=6×2.5=15 m/s=54km/h.
答案 不能超过54 km/h
点评 根据匀加速直线运动的速度公式即可得出答案.不过要注意加速度是负值.匀减速到零的直线运动可以反过来看做是初速度为零的匀加速直线运动,这样解起来很方便.车最终停下来,所以末速度为零,这一点容易忽略,导致缺少条件,解不出答案.
变式训练1
汽车以40 km/h的速度匀速行驶,
(1)若汽车以0.6 m/s2的加速度加速,则10 s后速度能达到多少?
(2)若汽车刹车以0.6 m/s2的加速度减速,则10 s 后速度减为多少?
(3)若汽车刹车以3 m/s2的加速度减速,则10 s后速度为多少?
解析 汽车做匀加速运动时,可直接应用公式v=v0+at,求10 s后的速度,汽车做匀减速运动时,要先验证减速为零时所用时间与10 s的关系,若大于10 s,则直接应用公式v=v0+at,若小于10 s,则10 s后的速度为零.
二、利用v-t图象分析物体的运动
例2 分析如图8-2所示的图线,物体在各段时间内做何种运动?哪一时间内的加速度最大?
图8-2
解析 v-t图象的斜率等于加速度的大小,负斜率表示加速度方向与规定的正方向相反.
由v-t图象的意义可知,物体在0~t1、t4~t5时间内做匀加速运动;t2~t3、t6~t7时间内做匀减速直线运动;在t1~t2、t5~t6时间内做匀速直线运动. v-t图象的斜率大小等于加速度大小,t2~t3段斜率最大,所以加速度最大.
答案 略
点评 速度大小的变化情况仅由速度和加速度方向的关系确定,不要认为加速度为负值,就做匀减速运动,如在本题中t4~t5时间内,虽然加速度为负值,但速度也为负值,即两者方向相同,物体做匀加速直线运动. 变式训练2
某质点的运动图象如图8-3所示,则质点( )
图8-3
A.在第1 s末运动方向发生变化
B.在第2 s末运动方向发生变化
C.在第2 s内速度越来越大
D.在第3 s内速度越来越大 解析 题图为v-t图象,由图可知,第1 s末速度达到最大,运动方向不变,选项A错误;第2 s末速度为零,然后反向加速,速度方向改变,选项B正确;第2 s内质点做减速运动,速度减小,选项C错误;第3 s内质点做反向的加速运动,速度增大,选项D正确.
答案 BD 三、物体分阶段运动问题
例3 发射卫星一般采用多级火箭,第一级火箭点火后,使卫星向上做匀加速运动的加速度为50 m/s2,燃烧30 s后第一级脱离,第二级火箭没有马上点火,所以卫星向上做加速度为10 m/s2的匀减速运动,10 s后第二级火箭启动,卫星的加速度为80 m/s2,这样经过1分半钟等第二级火箭脱离时,卫星的线速度为多大? 解析 整个过程中卫星的运动不是匀变速直线运动,但可以分解为三个匀变速直线运动处理.
第一级火箭燃烧完毕时的速度为:
v1=a1t1=1500 m/s
减速上升10 s后的速度为:
v2=v1-a2t2=1400 m/s
第二级火箭熄火时的速度为:
v3=v2+a3t3=8600 m/s.
答案 8600 m/s
点评 对于过程复杂的运动,我们可以将其分为几个简单运动,然后在每段运动中运用公式解答,从而达到化繁为简的目的. 变式训练3
升降机由静止开始以加速度a1匀加速上升2 s后速度达到3 m/s,接着匀速运动了一段时间,最后再以大小为1 m/s2的加速度匀减速上升才停下来.求:
(1)升降机匀加速上升的加速度a1.
(2)升降机匀减速上升的时间t2.
解析 设升降机向上运动的方向为正方向.
(1)匀加速上升过程,初速度v0=0,末速度v1=3 m/s,t1=2 s.根据vt=v0+at,得
答案 (1)1.5 m/s2 (2)3 s 互动平台
育才老师、粗心和细心同学关于匀减速运动规律的理解的对话
育才:汽车以36 km/h的速度行驶,刹车得到的加速度大小为4 m/s2,从刹车开始计时,前3 s内汽车通过的距离是多少?
粗心:应用位移公式不就迎刃而解了吗? 育才:3 s末的速度怎样了?
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
