2023届中考数学二轮专题复习:比例式探源 教案
文档属性
| 名称 | 2023届中考数学二轮专题复习:比例式探源 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 542.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-25 09:57:10 | ||
图片预览



文档简介
比例式探源教学设计
教学目标:1.探索等积式或比例式的源头找相似三角形(掌握证明线段等积式或比例式的一般思路与方法);
2.会用证明线段等积式或比例式的一般思路与方法求两条线段的比值或乘积和一条线段长度。
教学重点:掌握证明线段等积式或比例式的一般思路与方法。
教学难点:例2直接解决不了,需添辅助线来证明。
教学设计:
引言:前面我们刚学习完相似三角形的有关内容,平时我们在做题目过程中经常会遇到有关等积式或比例式的问题,许多同学可能解起来不顺手或者有些同学还感觉无从下手,所以今天这节课我们就一起来对比例式或等积式进行追本溯源。
第一环节(知识储备):
1.如图1,已知l1//l2//l3,你能完成以下填空吗?
设计意图:复习平行线分线段成比例定理,有利于学生在有平行线的图形中快速准确的得出相关的线段的比例式,从而能帮助学生准确分析问题。
2.相似三角形判定方法:
(1)定义;
(2)预备定理;
(3)有两个角对应相等的两个三角形相似;
(4)有两边对应成比例且夹角相等的两个三角形相似;
(5)三边对应成比例的两个三角形相似;
设计意图:在解决问题过程中,要得到比例式常常要先证明相应的两个三角形相似,所以复习相似三角形的的判定方法,有利于学生能根据题中和图中的条件快速准确的找到需要证明的两个相似三角形,从而能帮助学生准确分析问题。
第二个环节 追本溯源
引导学生分析思考:
(1)要证明这个等积式一般只要先证明什么?
(2)要证明这个比例式,一般考虑证明什么?
(3)证明哪两个三角形相似?你是怎么去找这两个三角形的?
预设(如果学生一下回答不上)就先分析1
师分析1:我们一下找不到的话,不妨我们先把这比例式中的四条线段在图形上进行标注起来,现在我们知道要找哪两个相似三角形了吗?
师分析2:如果我们不在图形上进行标注,直接从比例式中能找出这两个三角形吗?我们就可以从比例式的横向去找,先观察比例式横向上面的两条线段CD和BD有四个端点C、D、B、D,由于线段CD的端点D与线段BD的端点D是同一个点,即重合,所以实际上线段CD与BD只有三个不同的端点C,B,D,这三个不同的端点可能构成△BCD。我们接下来看比例式横向的下面两条线段AD,CD,这两条线段实际上也只有三个不同的端点A,C,D,一般来说可能构成△ACD.我们接下对照图形,看看这两个△BCD和△ACD在图形中存在不存在。发现存在,所以我们去考虑证明这两个三角形相似,这种从比例式的横向来确定三角形的方法,我们把它称为横定法。事实上,我们也可以从比例式的竖向来找两个三角形。我们先来看比例式左边的两条线段CD和AD,这两条线段实际上也只有3个不同的端点C,D,A.能构成△CDA.我们再来看比例式右边的两条线段CD和BD,这两条线段实际上有3个不同的端点C,D,B,能构成△CDB.接下来我们对照图形发现这两个三角形都存在,所以接下来我们去考虑证明这两个三角形是否相似,这种从比例式的竖向来确定三角形的方法,我们把它称为竖定法。再把解题的思路一起来梳理一下。
设计意图:利用引例引出用横定法和竖定法,从比例式中去找相似三角形的方法,帮助学生快速准确的找到需要证明的两个相似三角形,从而能帮助学生准确分析问题。
小结:要证明等积式的思路:一般先转化为比例式,再用横定法或竖定法找到两个三角形,再证明这两个三角形是否相似,如果这两个三角形相似,则问题得以解决(板书思路)。
小试牛刀:如图3,在ABCD中,E是AB延长线上一点,DE交BC于点F.
设计意图:1.继续巩固利用横定法或竖定法来找相似三角形;
2.证明等积式或比例式用用横定法或竖定法时让学生
明白有时候用横定法和竖定法都能找到相似三角形,但
有时两种方法中只有一种方法能找到相似三角形,而另一
种方法找不到相似三角形。
引导分析学思考生:
能用用横定法找到相似三角形吗?能用竖定法找到相似
三角形吗?如果都不能,那我们又该怎么办呢?
结合图形和已知我们可以考虑进行代换什么?代换的目的
是什么?(目的是为了满足横定法或竖定法的条件)
设计意图:让学生理解当我们所证的比例式都不满足用横定法或竖定法的条件时,我们就要考虑等量代换,代换之后使其比例式满足横定法或竖定法的条件,找到相似三角形,从而解决问题。其中等线段代换是一种重要方法,当然还有一些其他的代换,比如说等比代换,等积代换等等。
板书梳理:
引导学生分析:
这个比例式用横定法能得到哪两个三角形?△ACD与△CBD相似吗?(明显不相似)
那用竖定法呢?(一个△ACB和A、D、B三点在同一直线上构不成三角形)。
也就是说这个比例式比满足横定法的条件,但这个图形中的三角形明显不相似,所以我们自己去构造相似三角形,那怎么构造呢?
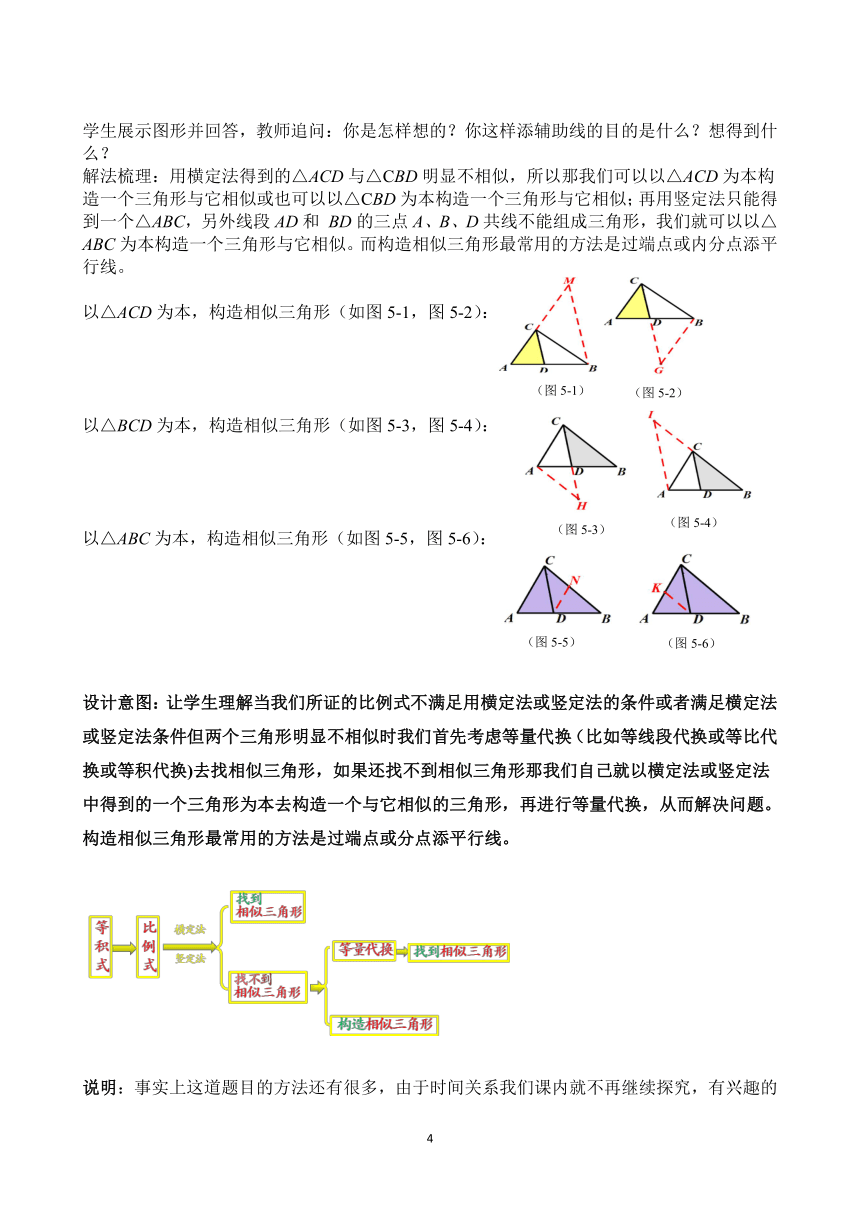
学生展示图形并回答,教师追问:你是怎样想的?你这样添辅助线的目的是什么?想得到什么?
解法梳理:用横定法得到的△ACD与△CBD明显不相似,所以那我们可以以△ACD为本构造一个三角形与它相似或也可以以△CBD为本构造一个三角形与它相似;再用竖定法只能得到一个△ABC,另外线段AD和 BD的三点A、B、D共线不能组成三角形,我们就可以以△ABC为本构造一个三角形与它相似。而构造相似三角形最常用的方法是过端点或内分点添平行线。
以△ACD为本,构造相似三角形(如图5-1,图5-2):
以△BCD为本,构造相似三角形(如图5-3,图5-4):
以△ABC为本,构造相似三角形(如图5-5,图5-6):
设计意图:让学生理解当我们所证的比例式不满足用横定法或竖定法的条件或者满足横定法或竖定法条件但两个三角形明显不相似时我们首先考虑等量代换(比如等线段代换或等比代换或等积代换)去找相似三角形,如果还找不到相似三角形那我们自己就以横定法或竖定法中得到的一个三角形为本去构造一个与它相似的三角形,再进行等量代换,从而解决问题。构造相似三角形最常用的方法是过端点或分点添平行线。
说明:事实上这道题目的方法还有很多,由于时间关系我们课内就不再继续探究,有兴趣的同学自己课后去作进一步探究。
第三个环节:知识梳理
问题:通过今天这节课的学习同学们有什么收获?(学生回答)
比例式追本溯源(证明等积式或比例式的一般思路与方法):要证明等积式一般先转化为比例式,再通过横定法或竖定法来找两个三角形,如果这两个三角形相似则问题解决;如果用横定法或竖定法找不到两个三角形或者找到的两个三角形不相似,则我们可以通过等量代换法(等线段代换、等比代换和等积代换法)来找到相似三角形,如果还找不到相似三角形那我们自己就以横定法或竖定法中得到的一个三角形为本去构造一个与它相似的三角形,再进行等量代换,从而解决问题。构造相似三角形最常用的方法是过端点或分点添平行线。
这就是证明等积式或比例式的一般思路与方法。当然还有一些特殊的方法,比如等面积法。
设计意图:对比例式追本溯源的过程进行梳理,得到证明等积式或比例式的一般思路与方法,让学生在今后解决等积式或比例式的有关问题时有方向、有途径、有方法,提高解题的效率。
第四个环节:学以致用(刚才我们都是证明比例式或等积式,那现在改成求两条线段的比值还能用今天所学的思路和方法来解决吗 )
如图6,在△ ABC中,点D在BC上,点F在边AB上,AD与CF
相交于点E.若AD是中线,E为AD的中点,
温馨提示:要求两条线段的比值,关键是找到隐含在题中与线段AF和BF有关的比例式。
解法展示:以图中线段AF为边的△AFE为本,构造三角形与△AFE相似(如图6-1至6-6):
以图中线段BF为边的△BFC为本,构造三角形与△BFC相似(如图6-7):
小结:在图形中找出以线段AF或BF为边的三角形,通过端点或分点作平行线构造一个三角形与以线段AF或BF为边的三角形相似,再通过等量代换去解决问题。一般的从所求比值或乘积有关的两条线段的比中选取一条线段作为一边在图形中找到相应的三角形,然后过端点或分点添一条平行线构造一个三角形与那个三角形相似,再通过等量代换,从而解决问题。
知识再梳理:运用线段等积式或比例式的一般思路与方法还可以求线段的长或两条线段的比值或乘积。
设计意图:1.所求线段长或所求两条线段的比或乘积时如何利用所求结论去构造相似三角形。
2.运用证明等积式或比例式的一般思路与方法还可以求有关线段的比值或长度或乘积,也就是说求线段的长度或者比值或乘积也可以运用证明等积式或比例式的一般思路与方法(将证明两个字改成运用)。
第五个环节:自我挑战---请你来编题
请你在上题(学以致用)的基础上对题目进行改编,并进行解答。
改编1:如图7,在△ ABC中,点D在BC上,点F在边AB上,AD与CF相交于点E.若AD是中线,
改编2:如图7,在△ ABC中,点D在BC上,点F在边AB上,AD与CF相交于点E.若AD是中线,
改编3:如图7,在△ ABC中,点D在BC上,点F在边AB上,AD与CF相交于点E.若AD是中线,
改编4:如图7,在△ ABC中,点D在BC上,点F在边AB上,AD与CF相交于点E.若AD是中线,
改编5:如图7,在△ ABC中,点D在BC上,点F在边AB上,AD与CF相交于点E.若AD是中线,
改编6:如图7,在△ ABC中,点D在BC上,点F在边AB上,AD与CF相交于点E.若AD是中线,
改编7:如图7,在△ ABC中,点D在BC上,点F在边AB上,AD与CF相交于点E.若AD是中线,
…………
小结:以上题目的不管如何改编,但解题的方法和思路还是一样的,一道题目通一类。巩固求两条线段的比值的思路和方法:在图形中找出所求线段或所求两条线段的比或乘积有关的两条线段中的一条线段为边的三角形,通过端点或分点作平行线构造一个三角形与这个三角形相似,再通过等量代换去解决问题。
老师编:如图8,在△ ABC中,点D,点F,点Q分别在边BC,边AB,边AC上,AD与FQ相交于点E. 若AD是中线,
留给同学们课后去思考并完成。
设计意图:让学有余力的同学能继续运用今天所学的方法和思路来挑战,进一步提升学生的运用此方法的水平与能力。
师小结:今天我们对比例式进行了追本溯源,相信今后同学们在证明等积式或比例式或求线段的长或求两条线段的比值或乘积时,运用我们今天这节课的一般思路与方法,大部分题目都能迎刃而解了。后面的题目作为今天这节课的课后作业,帮助同学们去巩固今天所学的知识。同学们,再见!
(图1)
(图2)
(图3)
(图4)
(图5)
(图5-2)
(图5-1)
(图5-4)
(图5-3)
(图5-6)
(图5-5)
(图6)
(图6-4)
(图6-1)
(图6-6)
(图6-5)
(图6-2)
(图6-3)
(图6-7)
(图7)
(图8)
教学目标:1.探索等积式或比例式的源头找相似三角形(掌握证明线段等积式或比例式的一般思路与方法);
2.会用证明线段等积式或比例式的一般思路与方法求两条线段的比值或乘积和一条线段长度。
教学重点:掌握证明线段等积式或比例式的一般思路与方法。
教学难点:例2直接解决不了,需添辅助线来证明。
教学设计:
引言:前面我们刚学习完相似三角形的有关内容,平时我们在做题目过程中经常会遇到有关等积式或比例式的问题,许多同学可能解起来不顺手或者有些同学还感觉无从下手,所以今天这节课我们就一起来对比例式或等积式进行追本溯源。
第一环节(知识储备):
1.如图1,已知l1//l2//l3,你能完成以下填空吗?
设计意图:复习平行线分线段成比例定理,有利于学生在有平行线的图形中快速准确的得出相关的线段的比例式,从而能帮助学生准确分析问题。
2.相似三角形判定方法:
(1)定义;
(2)预备定理;
(3)有两个角对应相等的两个三角形相似;
(4)有两边对应成比例且夹角相等的两个三角形相似;
(5)三边对应成比例的两个三角形相似;
设计意图:在解决问题过程中,要得到比例式常常要先证明相应的两个三角形相似,所以复习相似三角形的的判定方法,有利于学生能根据题中和图中的条件快速准确的找到需要证明的两个相似三角形,从而能帮助学生准确分析问题。
第二个环节 追本溯源
引导学生分析思考:
(1)要证明这个等积式一般只要先证明什么?
(2)要证明这个比例式,一般考虑证明什么?
(3)证明哪两个三角形相似?你是怎么去找这两个三角形的?
预设(如果学生一下回答不上)就先分析1
师分析1:我们一下找不到的话,不妨我们先把这比例式中的四条线段在图形上进行标注起来,现在我们知道要找哪两个相似三角形了吗?
师分析2:如果我们不在图形上进行标注,直接从比例式中能找出这两个三角形吗?我们就可以从比例式的横向去找,先观察比例式横向上面的两条线段CD和BD有四个端点C、D、B、D,由于线段CD的端点D与线段BD的端点D是同一个点,即重合,所以实际上线段CD与BD只有三个不同的端点C,B,D,这三个不同的端点可能构成△BCD。我们接下来看比例式横向的下面两条线段AD,CD,这两条线段实际上也只有三个不同的端点A,C,D,一般来说可能构成△ACD.我们接下对照图形,看看这两个△BCD和△ACD在图形中存在不存在。发现存在,所以我们去考虑证明这两个三角形相似,这种从比例式的横向来确定三角形的方法,我们把它称为横定法。事实上,我们也可以从比例式的竖向来找两个三角形。我们先来看比例式左边的两条线段CD和AD,这两条线段实际上也只有3个不同的端点C,D,A.能构成△CDA.我们再来看比例式右边的两条线段CD和BD,这两条线段实际上有3个不同的端点C,D,B,能构成△CDB.接下来我们对照图形发现这两个三角形都存在,所以接下来我们去考虑证明这两个三角形是否相似,这种从比例式的竖向来确定三角形的方法,我们把它称为竖定法。再把解题的思路一起来梳理一下。
设计意图:利用引例引出用横定法和竖定法,从比例式中去找相似三角形的方法,帮助学生快速准确的找到需要证明的两个相似三角形,从而能帮助学生准确分析问题。
小结:要证明等积式的思路:一般先转化为比例式,再用横定法或竖定法找到两个三角形,再证明这两个三角形是否相似,如果这两个三角形相似,则问题得以解决(板书思路)。
小试牛刀:如图3,在ABCD中,E是AB延长线上一点,DE交BC于点F.
设计意图:1.继续巩固利用横定法或竖定法来找相似三角形;
2.证明等积式或比例式用用横定法或竖定法时让学生
明白有时候用横定法和竖定法都能找到相似三角形,但
有时两种方法中只有一种方法能找到相似三角形,而另一
种方法找不到相似三角形。
引导分析学思考生:
能用用横定法找到相似三角形吗?能用竖定法找到相似
三角形吗?如果都不能,那我们又该怎么办呢?
结合图形和已知我们可以考虑进行代换什么?代换的目的
是什么?(目的是为了满足横定法或竖定法的条件)
设计意图:让学生理解当我们所证的比例式都不满足用横定法或竖定法的条件时,我们就要考虑等量代换,代换之后使其比例式满足横定法或竖定法的条件,找到相似三角形,从而解决问题。其中等线段代换是一种重要方法,当然还有一些其他的代换,比如说等比代换,等积代换等等。
板书梳理:
引导学生分析:
这个比例式用横定法能得到哪两个三角形?△ACD与△CBD相似吗?(明显不相似)
那用竖定法呢?(一个△ACB和A、D、B三点在同一直线上构不成三角形)。
也就是说这个比例式比满足横定法的条件,但这个图形中的三角形明显不相似,所以我们自己去构造相似三角形,那怎么构造呢?
学生展示图形并回答,教师追问:你是怎样想的?你这样添辅助线的目的是什么?想得到什么?
解法梳理:用横定法得到的△ACD与△CBD明显不相似,所以那我们可以以△ACD为本构造一个三角形与它相似或也可以以△CBD为本构造一个三角形与它相似;再用竖定法只能得到一个△ABC,另外线段AD和 BD的三点A、B、D共线不能组成三角形,我们就可以以△ABC为本构造一个三角形与它相似。而构造相似三角形最常用的方法是过端点或内分点添平行线。
以△ACD为本,构造相似三角形(如图5-1,图5-2):
以△BCD为本,构造相似三角形(如图5-3,图5-4):
以△ABC为本,构造相似三角形(如图5-5,图5-6):
设计意图:让学生理解当我们所证的比例式不满足用横定法或竖定法的条件或者满足横定法或竖定法条件但两个三角形明显不相似时我们首先考虑等量代换(比如等线段代换或等比代换或等积代换)去找相似三角形,如果还找不到相似三角形那我们自己就以横定法或竖定法中得到的一个三角形为本去构造一个与它相似的三角形,再进行等量代换,从而解决问题。构造相似三角形最常用的方法是过端点或分点添平行线。
说明:事实上这道题目的方法还有很多,由于时间关系我们课内就不再继续探究,有兴趣的同学自己课后去作进一步探究。
第三个环节:知识梳理
问题:通过今天这节课的学习同学们有什么收获?(学生回答)
比例式追本溯源(证明等积式或比例式的一般思路与方法):要证明等积式一般先转化为比例式,再通过横定法或竖定法来找两个三角形,如果这两个三角形相似则问题解决;如果用横定法或竖定法找不到两个三角形或者找到的两个三角形不相似,则我们可以通过等量代换法(等线段代换、等比代换和等积代换法)来找到相似三角形,如果还找不到相似三角形那我们自己就以横定法或竖定法中得到的一个三角形为本去构造一个与它相似的三角形,再进行等量代换,从而解决问题。构造相似三角形最常用的方法是过端点或分点添平行线。
这就是证明等积式或比例式的一般思路与方法。当然还有一些特殊的方法,比如等面积法。
设计意图:对比例式追本溯源的过程进行梳理,得到证明等积式或比例式的一般思路与方法,让学生在今后解决等积式或比例式的有关问题时有方向、有途径、有方法,提高解题的效率。
第四个环节:学以致用(刚才我们都是证明比例式或等积式,那现在改成求两条线段的比值还能用今天所学的思路和方法来解决吗 )
如图6,在△ ABC中,点D在BC上,点F在边AB上,AD与CF
相交于点E.若AD是中线,E为AD的中点,
温馨提示:要求两条线段的比值,关键是找到隐含在题中与线段AF和BF有关的比例式。
解法展示:以图中线段AF为边的△AFE为本,构造三角形与△AFE相似(如图6-1至6-6):
以图中线段BF为边的△BFC为本,构造三角形与△BFC相似(如图6-7):
小结:在图形中找出以线段AF或BF为边的三角形,通过端点或分点作平行线构造一个三角形与以线段AF或BF为边的三角形相似,再通过等量代换去解决问题。一般的从所求比值或乘积有关的两条线段的比中选取一条线段作为一边在图形中找到相应的三角形,然后过端点或分点添一条平行线构造一个三角形与那个三角形相似,再通过等量代换,从而解决问题。
知识再梳理:运用线段等积式或比例式的一般思路与方法还可以求线段的长或两条线段的比值或乘积。
设计意图:1.所求线段长或所求两条线段的比或乘积时如何利用所求结论去构造相似三角形。
2.运用证明等积式或比例式的一般思路与方法还可以求有关线段的比值或长度或乘积,也就是说求线段的长度或者比值或乘积也可以运用证明等积式或比例式的一般思路与方法(将证明两个字改成运用)。
第五个环节:自我挑战---请你来编题
请你在上题(学以致用)的基础上对题目进行改编,并进行解答。
改编1:如图7,在△ ABC中,点D在BC上,点F在边AB上,AD与CF相交于点E.若AD是中线,
改编2:如图7,在△ ABC中,点D在BC上,点F在边AB上,AD与CF相交于点E.若AD是中线,
改编3:如图7,在△ ABC中,点D在BC上,点F在边AB上,AD与CF相交于点E.若AD是中线,
改编4:如图7,在△ ABC中,点D在BC上,点F在边AB上,AD与CF相交于点E.若AD是中线,
改编5:如图7,在△ ABC中,点D在BC上,点F在边AB上,AD与CF相交于点E.若AD是中线,
改编6:如图7,在△ ABC中,点D在BC上,点F在边AB上,AD与CF相交于点E.若AD是中线,
改编7:如图7,在△ ABC中,点D在BC上,点F在边AB上,AD与CF相交于点E.若AD是中线,
…………
小结:以上题目的不管如何改编,但解题的方法和思路还是一样的,一道题目通一类。巩固求两条线段的比值的思路和方法:在图形中找出所求线段或所求两条线段的比或乘积有关的两条线段中的一条线段为边的三角形,通过端点或分点作平行线构造一个三角形与这个三角形相似,再通过等量代换去解决问题。
老师编:如图8,在△ ABC中,点D,点F,点Q分别在边BC,边AB,边AC上,AD与FQ相交于点E. 若AD是中线,
留给同学们课后去思考并完成。
设计意图:让学有余力的同学能继续运用今天所学的方法和思路来挑战,进一步提升学生的运用此方法的水平与能力。
师小结:今天我们对比例式进行了追本溯源,相信今后同学们在证明等积式或比例式或求线段的长或求两条线段的比值或乘积时,运用我们今天这节课的一般思路与方法,大部分题目都能迎刃而解了。后面的题目作为今天这节课的课后作业,帮助同学们去巩固今天所学的知识。同学们,再见!
(图1)
(图2)
(图3)
(图4)
(图5)
(图5-2)
(图5-1)
(图5-4)
(图5-3)
(图5-6)
(图5-5)
(图6)
(图6-4)
(图6-1)
(图6-6)
(图6-5)
(图6-2)
(图6-3)
(图6-7)
(图7)
(图8)
同课章节目录
