2.2简谐运动的描述(共28张ppt)人教版(2019)选择性必修第一册第二章 机械振动
文档属性
| 名称 | 2.2简谐运动的描述(共28张ppt)人教版(2019)选择性必修第一册第二章 机械振动 |  | |
| 格式 | pptx | ||
| 文件大小 | 29.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-05-25 08:24:42 | ||
图片预览





文档简介
(共28张PPT)
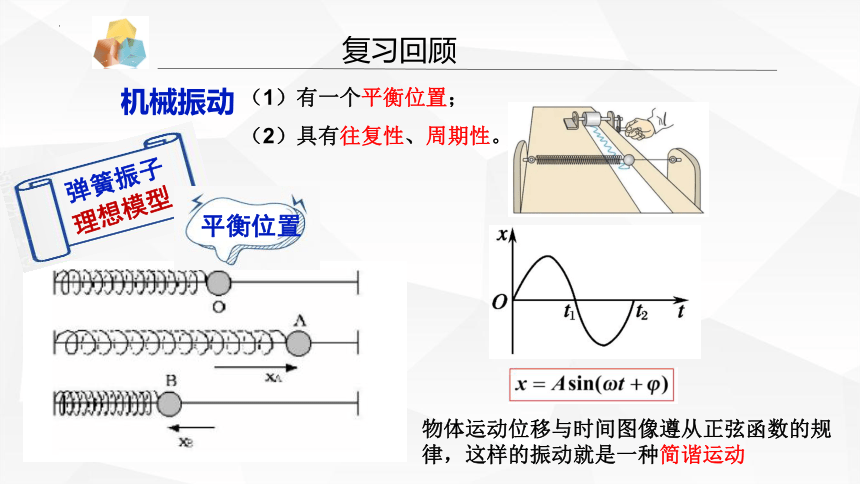
1.2 简谐运动的描述
第二章 机械振动
【学习目标】
弹簧振子
理想模型
复习回顾
机械振动
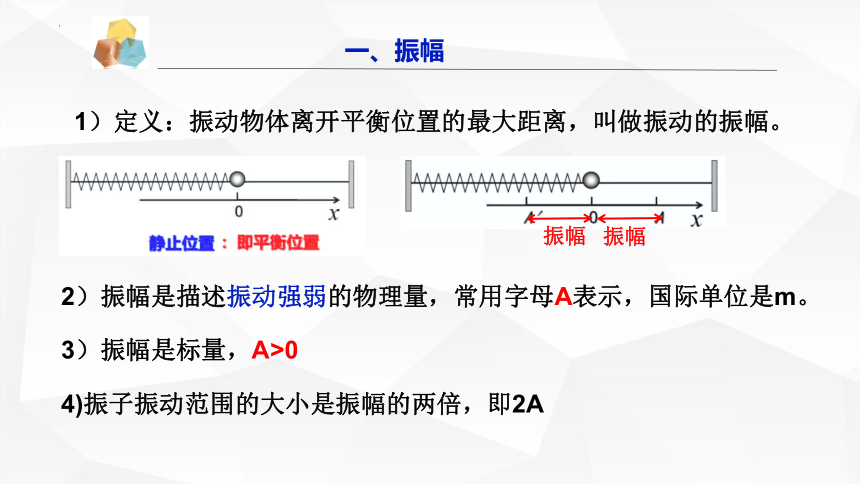
(1)有一个平衡位置; (2)具有往复性、周期性。
平衡位置
物体运动位移与时间图像遵从正弦函数的规律,这样的振动就是一种简谐运动
以下两同相同的弹簧振子的运动范围有何不同?
观察1
一、振幅
1)定义:振动物体离开平衡位置的最大距离,叫做振动的振幅。
振幅
振幅
2)振幅是描述振动强弱的物理量,常用字母A表示,国际单位是m。
3)振幅是标量,A>0
4)振子振动范围的大小是振幅的两倍,即2A
区分振幅与位移
对于一个给定的振动:
1、振子的位移是偏离平衡位置的距离,故时刻在变化;但振幅是不变的。
2、位移是矢量,振幅是标量,它等于最大位移的数值。
观察,弹簧振子的运动最显著的特点是什么?
对称性
周期性
往复运动
观察2
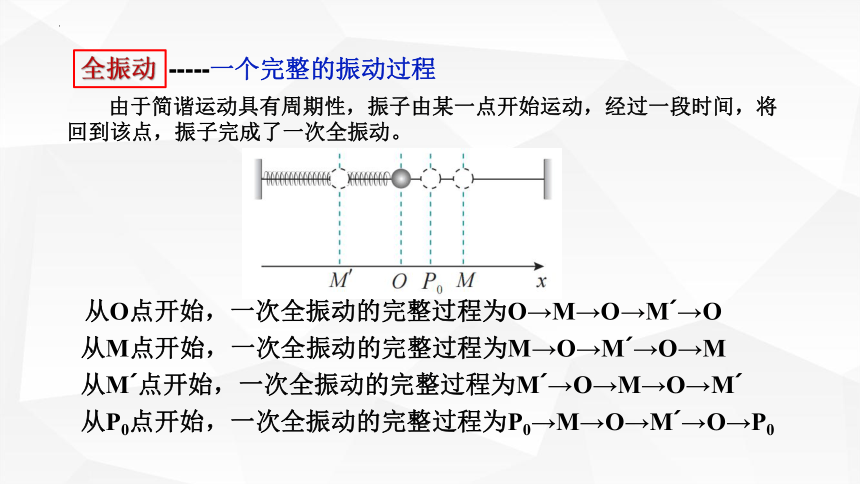
-----一个完整的振动过程
全振动
由于简谐运动具有周期性,振子由某一点开始运动,经过一段时间,将回到该点,振子完成了一次全振动。
从O点开始,一次全振动的完整过程为O→M→O→M →O
从M点开始,一次全振动的完整过程为M→O→M →O→M
从M 点开始,一次全振动的完整过程为M →O→M→O→M
从P0点开始,一次全振动的完整过程为P0→M→O→M →O→P0
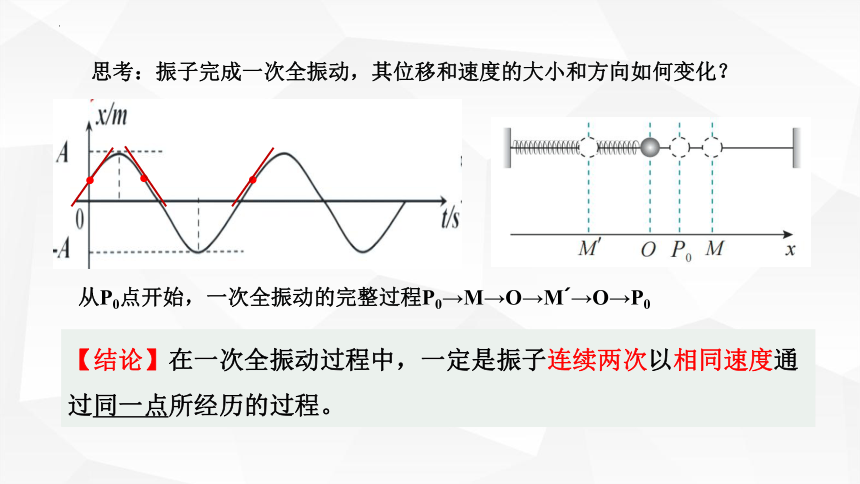
思考:振子完成一次全振动,其位移和速度的大小和方向如何变化?
从P0点开始,一次全振动的完整过程P0→M→O→M →O→P0
●
●
●
【结论】在一次全振动过程中,一定是振子连续两次以相同速度通过同一点所经历的过程。
二、周期和频率
2)周期T:做简谐运动的物体完成一次全振动所需的时间,单位:s。
3)频率f:单位时间内完成的全振动的次数,单位:Hz。
4)周期和频率之间的关系:
5)周期越小,频率越大,振动越快
1)表示振动快慢
注意! 区分振动的快慢和振动物体运动的快慢
振动物体运动的快慢是指某时刻振动物体的速度,它是随时间变化的;
对于一个给定的振动,周期和频率是从整体上描述振动快慢的物理量。
振幅与路程的关系
思考:一个周期内,路程和振幅有什么定量关系呢?
半个周期呢?四分之一周期呢?
一个周期内,路程=4A
半个周期内,路程=2A
●
快
慢
●
●
★简谐运动是变速运动!
注意:1/4个周期内的路程可以等于A,可以大于A,也可以小于A。只有初始时刻在平衡位置和最大位移处时,1/4周期内的路程等于A.
1/4T的路程和振幅没有定量关系
如图所示,一竖直弹簧上端固定,下端悬挂钢球。把钢球从平衡位置向下拉一段距离 A,放手让其运动,A 就是振动的振幅。给你一个秒表,怎样测出振子的振动周期T?
为了减小测量误差,采用累积法测振子的振动周期T,即用秒表测出发生n次全振动所用的总时间t,可得周期为
T=t/n
通过在一定时间内比较振动的次数判断周期的大小
做一做
问题:简谐振动的周期与哪些因素有关呢?
猜想:.....
结论:弹簧振子的周期由振动系统本身的质量和劲度系数决定,而与振幅无关,所以常把周期和频率叫做固有周期和固有频率。
实验结果:
(不要求掌握)
两个相同的弹簧振子先后开始振动,观察,它们的振动有何不同呢?能否用之前学过的物理量来描述这种不同呢?
观察3
1)在物理学中,我们用不同的相位来描述周期性运动在各个时刻所处的不同状态。
三、相 位
2)物理意义:是表示物体振动步调的物理量,用相位来描述简谐运动在各个时刻所处的不同状态(或不同位置)
乙振子的相位落后于甲振子的相位。
前面我们研究过的这两个弹簧振子的相位有什么特点?
步调一致,同时到达一个全振动的相同阶段,任意时刻相位相同
四、简谐运动的表达式
根据数学知识,写出如下简谐运动的x-t图象对应的函数关系式并思考,式中各个物理量的含义是什么?
振幅
相位
初相位
相位中的“ωt+φ”的单位应该是什么?
圆频率
试计算,时间t每增加多少,sin(ωt+φ)这个量循环变化一次?
经过一个周期t1增加到t2,周期T=t2-t1,
sin(ωt+φ)循环一次,则(ωt1+φ)-(ωt2+φ)=2π
ω
★对简谐运动的表达式的理解
1)A为简谐运动的振幅。表示简谐运动的强弱。
2)ω叫圆频率,表示简谐运动的快慢。
3)"ωt+φ”叫简谐运动的相位。它是随时间t不断变化的物理量,表示简谐运动所处的状态。
φ叫初相位,即t=0时的相位。
4)相位差:两个简谐运动的相位差,简称相差
△φ=(ω1t+φ1)-(ω2t+φ2)
(2)取值范围:-π≤△φ≤π
△φ=0,表明两振动步调完全相同,称为同相。
△φ=-π,表明两振动步调完全相反,称为反相。
△φ>0,表示振动1比振动2超前△φ。
△φ<0,表示振动1比振动2落后△φ。
(1)若相同频率,则相位差为:△φ=φ1-φ2
2.图中振子Q的振动比振子P的振动超前了多少个周期?
1.甲和乙两个简谐运动的相位差为π/2(φ甲-φ乙=π/2),意味着什么?
意味着乙总是比甲滞后1/4个周期或1/4次全振动。
方法:左右平移,左加右减。
t=0 振子Q
t=0 振子p
总结思考:
经过一个的全振动过程,各个物理量有什么显著变化?
振动特征:一个完整的振动过程
在一次全振动过程中,一定是振子连续两次以相同速度通过同一点,所经历的过程
时间特征:历时一个周期T
路程特征:振幅的4倍
相位特征:增加了2π
【课堂练习】
(多选)例题1:两个简谐振动,其表达式分别是:x1=3sin(100πt+π/3)cm,x2=6sin(100πt+π/4)cm,下列说法正确的是( )
A.它们的振幅相同 B.它们的周期相同
C.它们的相位差恒定 D.它们的振动步调一致
BC
【课堂练习】
例题2:如图,写出振动方程 。
祝同学们学习愉快
1.2 简谐运动的描述
第二章 机械振动
【学习目标】
弹簧振子
理想模型
复习回顾
机械振动
(1)有一个平衡位置; (2)具有往复性、周期性。
平衡位置
物体运动位移与时间图像遵从正弦函数的规律,这样的振动就是一种简谐运动
以下两同相同的弹簧振子的运动范围有何不同?
观察1
一、振幅
1)定义:振动物体离开平衡位置的最大距离,叫做振动的振幅。
振幅
振幅
2)振幅是描述振动强弱的物理量,常用字母A表示,国际单位是m。
3)振幅是标量,A>0
4)振子振动范围的大小是振幅的两倍,即2A
区分振幅与位移
对于一个给定的振动:
1、振子的位移是偏离平衡位置的距离,故时刻在变化;但振幅是不变的。
2、位移是矢量,振幅是标量,它等于最大位移的数值。
观察,弹簧振子的运动最显著的特点是什么?
对称性
周期性
往复运动
观察2
-----一个完整的振动过程
全振动
由于简谐运动具有周期性,振子由某一点开始运动,经过一段时间,将回到该点,振子完成了一次全振动。
从O点开始,一次全振动的完整过程为O→M→O→M →O
从M点开始,一次全振动的完整过程为M→O→M →O→M
从M 点开始,一次全振动的完整过程为M →O→M→O→M
从P0点开始,一次全振动的完整过程为P0→M→O→M →O→P0
思考:振子完成一次全振动,其位移和速度的大小和方向如何变化?
从P0点开始,一次全振动的完整过程P0→M→O→M →O→P0
●
●
●
【结论】在一次全振动过程中,一定是振子连续两次以相同速度通过同一点所经历的过程。
二、周期和频率
2)周期T:做简谐运动的物体完成一次全振动所需的时间,单位:s。
3)频率f:单位时间内完成的全振动的次数,单位:Hz。
4)周期和频率之间的关系:
5)周期越小,频率越大,振动越快
1)表示振动快慢
注意! 区分振动的快慢和振动物体运动的快慢
振动物体运动的快慢是指某时刻振动物体的速度,它是随时间变化的;
对于一个给定的振动,周期和频率是从整体上描述振动快慢的物理量。
振幅与路程的关系
思考:一个周期内,路程和振幅有什么定量关系呢?
半个周期呢?四分之一周期呢?
一个周期内,路程=4A
半个周期内,路程=2A
●
快
慢
●
●
★简谐运动是变速运动!
注意:1/4个周期内的路程可以等于A,可以大于A,也可以小于A。只有初始时刻在平衡位置和最大位移处时,1/4周期内的路程等于A.
1/4T的路程和振幅没有定量关系
如图所示,一竖直弹簧上端固定,下端悬挂钢球。把钢球从平衡位置向下拉一段距离 A,放手让其运动,A 就是振动的振幅。给你一个秒表,怎样测出振子的振动周期T?
为了减小测量误差,采用累积法测振子的振动周期T,即用秒表测出发生n次全振动所用的总时间t,可得周期为
T=t/n
通过在一定时间内比较振动的次数判断周期的大小
做一做
问题:简谐振动的周期与哪些因素有关呢?
猜想:.....
结论:弹簧振子的周期由振动系统本身的质量和劲度系数决定,而与振幅无关,所以常把周期和频率叫做固有周期和固有频率。
实验结果:
(不要求掌握)
两个相同的弹簧振子先后开始振动,观察,它们的振动有何不同呢?能否用之前学过的物理量来描述这种不同呢?
观察3
1)在物理学中,我们用不同的相位来描述周期性运动在各个时刻所处的不同状态。
三、相 位
2)物理意义:是表示物体振动步调的物理量,用相位来描述简谐运动在各个时刻所处的不同状态(或不同位置)
乙振子的相位落后于甲振子的相位。
前面我们研究过的这两个弹簧振子的相位有什么特点?
步调一致,同时到达一个全振动的相同阶段,任意时刻相位相同
四、简谐运动的表达式
根据数学知识,写出如下简谐运动的x-t图象对应的函数关系式并思考,式中各个物理量的含义是什么?
振幅
相位
初相位
相位中的“ωt+φ”的单位应该是什么?
圆频率
试计算,时间t每增加多少,sin(ωt+φ)这个量循环变化一次?
经过一个周期t1增加到t2,周期T=t2-t1,
sin(ωt+φ)循环一次,则(ωt1+φ)-(ωt2+φ)=2π
ω
★对简谐运动的表达式的理解
1)A为简谐运动的振幅。表示简谐运动的强弱。
2)ω叫圆频率,表示简谐运动的快慢。
3)"ωt+φ”叫简谐运动的相位。它是随时间t不断变化的物理量,表示简谐运动所处的状态。
φ叫初相位,即t=0时的相位。
4)相位差:两个简谐运动的相位差,简称相差
△φ=(ω1t+φ1)-(ω2t+φ2)
(2)取值范围:-π≤△φ≤π
△φ=0,表明两振动步调完全相同,称为同相。
△φ=-π,表明两振动步调完全相反,称为反相。
△φ>0,表示振动1比振动2超前△φ。
△φ<0,表示振动1比振动2落后△φ。
(1)若相同频率,则相位差为:△φ=φ1-φ2
2.图中振子Q的振动比振子P的振动超前了多少个周期?
1.甲和乙两个简谐运动的相位差为π/2(φ甲-φ乙=π/2),意味着什么?
意味着乙总是比甲滞后1/4个周期或1/4次全振动。
方法:左右平移,左加右减。
t=0 振子Q
t=0 振子p
总结思考:
经过一个的全振动过程,各个物理量有什么显著变化?
振动特征:一个完整的振动过程
在一次全振动过程中,一定是振子连续两次以相同速度通过同一点,所经历的过程
时间特征:历时一个周期T
路程特征:振幅的4倍
相位特征:增加了2π
【课堂练习】
(多选)例题1:两个简谐振动,其表达式分别是:x1=3sin(100πt+π/3)cm,x2=6sin(100πt+π/4)cm,下列说法正确的是( )
A.它们的振幅相同 B.它们的周期相同
C.它们的相位差恒定 D.它们的振动步调一致
BC
【课堂练习】
例题2:如图,写出振动方程 。
祝同学们学习愉快
