1.2动量定理的应用(第2课时)
文档属性
| 名称 | 1.2动量定理的应用(第2课时) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-05-25 10:06:51 | ||
图片预览







文档简介
(共26张PPT)
Theorem of Momentum
第一章 动量守恒定律
第2节动量定理的应用
一、动量定理
I =F t
1. 冲量:
物体在一个过程中所受合外力的冲量等于它在这个过程始末的动量变化量。
I = p ′- p = p
合
2. 动量定理:
(1) 不仅适用于恒力,也适用于随时间变化的变力;对于变力,动量定理中的F应理解为变力在作用时间内的平均值;
(2) 不仅可以解决匀变速直线运动的问题,还可以解决曲线运动中的有关问题,简化较难的计算问题;
(3) 不仅适用于宏观低速物体,也适用于微观现象和变速运动问题。
3. 适用范围:
4. 动量定理是矢量式,不需要考虑中间过程,只考虑初末状态。
5. 合外力的冲量方向与速度变化量的方向一致。
用 解决生活中的实际问题
I = p ′- p
合
例题1.一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒击打后,反向水平飞回,速度的大小为45m/s。若球棒与垒球的作用时间为0.002s,球棒对垒球的平均作用力是多大?
一、动量定理
解:以垒球飞向球棒时的方向为正。
则垒球的初动量为:
p = mv = 0.18×25 kg·m/s = 4.5 kg·m/s
p′= mv′=- 0.18×45 kg·m/s =- 8.1 kg·m/s
则垒球的末动量为:
由动量定理知垒球所受的平均作用力为:
负号表示力的方向与垒球飞来的方向相反。
动量定理的应用步骤
1. 确定研究对象:一般为单个物体;
4. 选定正方向,确定在物理过程中研究对象的动量的变化;
5. 根据动量定理列方程,统一单位后代入数据求解。
2. 明确物理过程:受力分析,求出合外力的冲量;
3. 明确研究对象的初末状态及相应的动量;
用 解决生活中的实际问题
I = p ′- p
合
一、动量定理
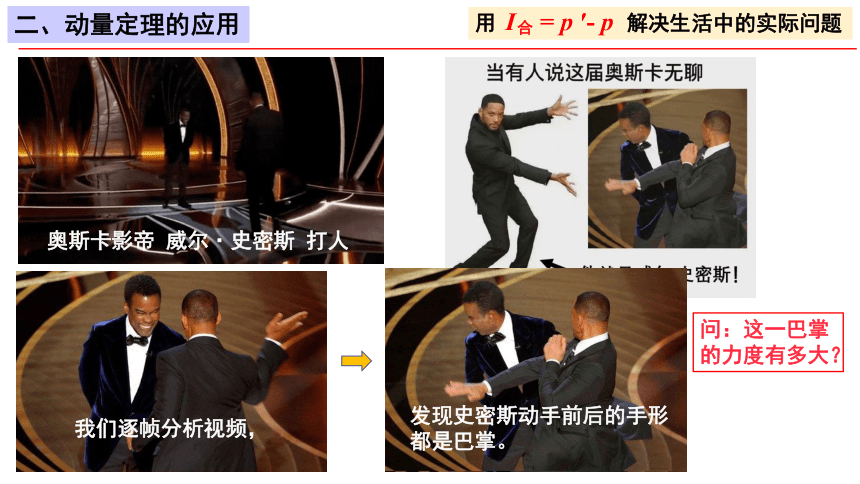
二、动量定理的应用
奥斯卡影帝 威尔·史密斯 打人
我们逐帧分析视频,
发现史密斯动手前后的手形
都是巴掌。
问:这一巴掌
的力度有多大?
用 解决生活中的实际问题
I = p ′- p
合
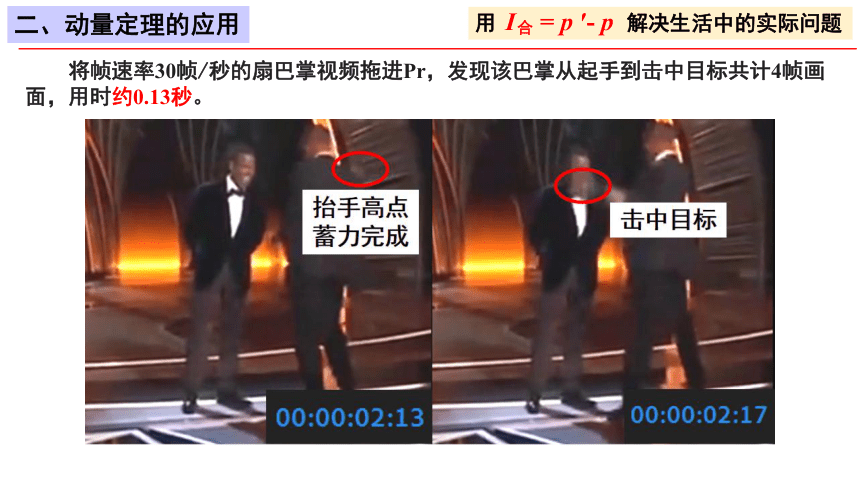
将帧速率30帧/秒的扇巴掌视频拖进Pr,发现该巴掌从起手到击中目标共计4帧画面,用时约0.13秒。
用 解决生活中的实际问题
I = p ′- p
合
二、动量定理的应用
我们假设巴掌做从0开始做匀加速直线运动,再根据目测求得巴掌的运动距离,则可以求出巴掌呼到脸上的速度。
v
t
v
max
t ≈ 0.13 s
0
威尔史密斯巴掌在空中的轨迹可近似为一段圆弧 l ,
手臂摆幅 α ≈ 90°,臂长 h ≈ 70 cm ,
则:圆弧 l = α· h ≈ 1.1 m ,
用 解决生活中的实际问题
I = p ′- p
合
由匀加速直线运动,可得:
则巴掌到达脸处瞬间的速度:
二、动量定理的应用
这一掌与主持人面部的接触时间不到1帧(1/30秒),假设一掌打完速度为0;
目测威尔·史密斯体重约为90kg,而正常男生的一只手约占体重的0.33%,则史密斯一只手的质量约为0.297kg,确实下手很重...
根据动量定理及牛顿第三定律,得:
这比一箱24瓶矿泉水(重约14kg)直接压在脸上还痛。大概是这么痛:
用 解决生活中的实际问题
I = p ′- p
合
二、动量定理的应用
传接球时为何不自觉地弯曲手臂?
用 解决生活中的实际问题
I = p ′- p
合
二、动量定理的应用
铺在地上的毛巾可以延长作用时间,
当物体的动量变化量一定时,时间越长,作用力就越小,
所以鸡蛋不会摔碎。
用 解决生活中的实际问题
I = p ′- p
合
二、动量定理的应用
1. 解释有关现象
越长,
一定时,
越短,
则F越小。
则F越大。
一定时,
例题2. 若一个50 g的鸡蛋从20m坠下,与地面的撞击时间约为0.001s,则该鸡蛋对地面产生的冲击力约为( )
A.10 N B.102 N C.103 N D.104 N
C
思考:若地面平铺一层海绵,使得撞击时间变为0.1s,冲击力?
10N
—— 缓冲作用
用 解决生活中的实际问题
I = p ′- p
合
二、动量定理的应用
例题3. 质量为60 kg的建筑工人,不慎从高空跌下,幸好弹性安全带的保护使他悬挂起来.已知弹性安全带的缓冲时间是1.5 s,安全带自然长度为5 m,g取10 m/s2,求安全带所受的平均冲力的大小?
v
0
(规定向下为正方向)
F = 1000N
解:
刚刚伸直
最低点
用 解决生活中的实际问题
I = p ′- p
合
二、动量定理的应用
二、动量定理的应用
用动量定理处理多过程问题
[导学探究]在水平恒力F=30N的作用下,质量m=5kg的物体由静止开始沿水平面运动.已知物体与水平面间的动摩擦因数μ=0.2,若F作用6s后撤去,撤去F后物体还能向前运动多长时间才停止?(g取10 m/s2) 用动量定理分别从分段及全程两个角度进行求解.
二、动量定理的应用
用动量定理处理多过程问题
[例题1]一现代仿制的地动仪,龙口中的铜珠到蟾蜍口的距离为h,当感知到地震时,质量为m的铜珠(初速度为零)离开龙口,落入蟾蜍口中,与蟾蜍口碰撞的时间约为t,重力加速度为g,不计空气阻力,则铜珠对蟾蜍口产生的冲击力大小约为( )
二、动量定理的应用
用动量定理处理多过程问题
[例题2]某消防队员从一平台上跳下,下落1s后双脚触地,接着他用双腿弯曲的方法缓冲,使自身重心又下降了0.2 s,在着地过程中地面对他双脚的平均作用力约为( )
二、动量定理的应用
用动量定理处理流体问题
(1)建立“柱体”模型.对于流体,可沿流速v的方向选取一段柱形流体,设在Δt时间内通过某一横截面积为S的流体长度 Δl=v·Δt,如图,若流体的密度为ρ,那么在这段时间内流过该截面的流体的质量为 Δm=ρSΔl=ρSvΔt .
(2)运用动量定理,即流体微元所受的合力的冲量等于微元动量的增量,即F合Δt=Δp. (Δt足够短时,重力可忽略不计)
二、动量定理的应用
用动量定理处理流体问题
[例题3]水力采煤时,用水枪在高压下喷出的强力水柱冲击煤层.设水柱直径为d=30 cm,水速为v=50m/s.假设水柱射在煤层的表面上,冲击煤层后水的速度变为零.求水柱对煤层的平均冲击力的大小.(水的密度ρ=1.0×103 kg/m3,结果保留三位有效数字)
二、动量定理的应用
用动量定理处理流体问题
[例题4]假如有一宇宙飞船,它的正面面积为S=0.98 m2,以v=2×103 m/s的速度进入宇宙微粒尘区,尘区每1 m3空间有一微粒,每一微粒平均质量m=2×10-4 g,若要使飞船速度保持不变,飞船的牵引力应增加多少?(设微粒与飞船相碰后附着到飞船上)
例题4.一铁块压着一纸条放在水平桌面上,当以速度v抽出纸条后,铁块掉在地上的P点.若以2v速度抽出纸条,则铁块落地点为( )
A.仍在P点
B.在P点左边
C.在P点右边不远处
D.在P点右边原水平位移的两倍处
B
用 解决生活中的实际问题
I = p ′- p
合
二、动量定理的应用
冲量
功
区
别
公式
标矢性
意义
正负
作用效果
单位
某个力对物体有冲量,不一定做功;某个力对物体做了功,一定有冲量。
N·S
I=Ft
W=Fxcos θ
矢量
标量
N·m 或(J)
力对时间的积累, 对应一段时间
在F-t图像中可以用面积表示
力对位移的积累, 对应一段位移
在F-x图像中可以用面积表示
正负表示与正方向相同或相反
正负表示动力做功或阻力做功
改变物体的动量
改变物体的动能
F
t
O
F
t
x
F
O
F
x
三、冲量与功
1.如图,一物体静止在水平地面上,受到与水平方向成θ角的恒定拉力F作用时间t后,物体仍保持静止。以下看法种正确的是( )
四、练习与应用
教材 第10页
A.物体所受拉力F的冲量方向水平向右
B.物体所受拉力F的冲量大小是Ftcos θ
C.物体所受摩擦力的冲量大小为0
D.物体所受合力的冲量大小为0
2.如图,体操运动员在落地时总要屈腿,这是为什么?
四、练习与应用
教材 第10页
3.如图,用0.5 kg的铁锤钉钉子,打击前铁锤的速度为4m/s。打击后铁锤的速度变为0,设打击时间为0.01s。
(1)不计铁锤所受的重力,铁锤钉钉子的平均作用力是多大?
(2)考虑铁锤所受的重力,铁锤钉钉子的平均作用力是多大?
(3)你分析一下,在计算铁锤钉钉子的平均作用力时,
在什么情况下可以不计铁锤所受的重力。
四、练习与应用
教材 第10页
4.一个质量为10kg的物体,以10m/s的速度做直线运动,受到一个反向的作用力F,经过4s,速度变为反向2m/s。这个力是多大?
四、练习与应用
教材 第10页
5.一个质量为60kg的蹦床运动员,从离水平网面3.2m高处自由下落,着网后沿竖直方向蹦回到离水平网面5.0m高处。已知运动员与网接触的时间为0.8s,g取10m/s2。
(1)求运动员与网接触的这段时间内动量的变化量;
(2)求网对运动员的平均作用力大小;
(3)求从自由下落开始到蹦回离水平网面5.0 m高处这一过程中运动员所受重力冲量、弹力冲量。
四、练习与应用
教材 第10页
6.曾经有一则新闻报道,一名4岁儿童从3层高的楼房掉下来,被一名见义勇为的青年接住。请你估算一下,儿童受到的合力的冲量是多大?设儿童与青年之间的相互作用时间为0.1s,则儿童受到的合力的平均值有多大?
四、练习与应用
教材 第10页
Theorem of Momentum
第一章 动量守恒定律
第2节动量定理的应用
一、动量定理
I =F t
1. 冲量:
物体在一个过程中所受合外力的冲量等于它在这个过程始末的动量变化量。
I = p ′- p = p
合
2. 动量定理:
(1) 不仅适用于恒力,也适用于随时间变化的变力;对于变力,动量定理中的F应理解为变力在作用时间内的平均值;
(2) 不仅可以解决匀变速直线运动的问题,还可以解决曲线运动中的有关问题,简化较难的计算问题;
(3) 不仅适用于宏观低速物体,也适用于微观现象和变速运动问题。
3. 适用范围:
4. 动量定理是矢量式,不需要考虑中间过程,只考虑初末状态。
5. 合外力的冲量方向与速度变化量的方向一致。
用 解决生活中的实际问题
I = p ′- p
合
例题1.一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒击打后,反向水平飞回,速度的大小为45m/s。若球棒与垒球的作用时间为0.002s,球棒对垒球的平均作用力是多大?
一、动量定理
解:以垒球飞向球棒时的方向为正。
则垒球的初动量为:
p = mv = 0.18×25 kg·m/s = 4.5 kg·m/s
p′= mv′=- 0.18×45 kg·m/s =- 8.1 kg·m/s
则垒球的末动量为:
由动量定理知垒球所受的平均作用力为:
负号表示力的方向与垒球飞来的方向相反。
动量定理的应用步骤
1. 确定研究对象:一般为单个物体;
4. 选定正方向,确定在物理过程中研究对象的动量的变化;
5. 根据动量定理列方程,统一单位后代入数据求解。
2. 明确物理过程:受力分析,求出合外力的冲量;
3. 明确研究对象的初末状态及相应的动量;
用 解决生活中的实际问题
I = p ′- p
合
一、动量定理
二、动量定理的应用
奥斯卡影帝 威尔·史密斯 打人
我们逐帧分析视频,
发现史密斯动手前后的手形
都是巴掌。
问:这一巴掌
的力度有多大?
用 解决生活中的实际问题
I = p ′- p
合
将帧速率30帧/秒的扇巴掌视频拖进Pr,发现该巴掌从起手到击中目标共计4帧画面,用时约0.13秒。
用 解决生活中的实际问题
I = p ′- p
合
二、动量定理的应用
我们假设巴掌做从0开始做匀加速直线运动,再根据目测求得巴掌的运动距离,则可以求出巴掌呼到脸上的速度。
v
t
v
max
t ≈ 0.13 s
0
威尔史密斯巴掌在空中的轨迹可近似为一段圆弧 l ,
手臂摆幅 α ≈ 90°,臂长 h ≈ 70 cm ,
则:圆弧 l = α· h ≈ 1.1 m ,
用 解决生活中的实际问题
I = p ′- p
合
由匀加速直线运动,可得:
则巴掌到达脸处瞬间的速度:
二、动量定理的应用
这一掌与主持人面部的接触时间不到1帧(1/30秒),假设一掌打完速度为0;
目测威尔·史密斯体重约为90kg,而正常男生的一只手约占体重的0.33%,则史密斯一只手的质量约为0.297kg,确实下手很重...
根据动量定理及牛顿第三定律,得:
这比一箱24瓶矿泉水(重约14kg)直接压在脸上还痛。大概是这么痛:
用 解决生活中的实际问题
I = p ′- p
合
二、动量定理的应用
传接球时为何不自觉地弯曲手臂?
用 解决生活中的实际问题
I = p ′- p
合
二、动量定理的应用
铺在地上的毛巾可以延长作用时间,
当物体的动量变化量一定时,时间越长,作用力就越小,
所以鸡蛋不会摔碎。
用 解决生活中的实际问题
I = p ′- p
合
二、动量定理的应用
1. 解释有关现象
越长,
一定时,
越短,
则F越小。
则F越大。
一定时,
例题2. 若一个50 g的鸡蛋从20m坠下,与地面的撞击时间约为0.001s,则该鸡蛋对地面产生的冲击力约为( )
A.10 N B.102 N C.103 N D.104 N
C
思考:若地面平铺一层海绵,使得撞击时间变为0.1s,冲击力?
10N
—— 缓冲作用
用 解决生活中的实际问题
I = p ′- p
合
二、动量定理的应用
例题3. 质量为60 kg的建筑工人,不慎从高空跌下,幸好弹性安全带的保护使他悬挂起来.已知弹性安全带的缓冲时间是1.5 s,安全带自然长度为5 m,g取10 m/s2,求安全带所受的平均冲力的大小?
v
0
(规定向下为正方向)
F = 1000N
解:
刚刚伸直
最低点
用 解决生活中的实际问题
I = p ′- p
合
二、动量定理的应用
二、动量定理的应用
用动量定理处理多过程问题
[导学探究]在水平恒力F=30N的作用下,质量m=5kg的物体由静止开始沿水平面运动.已知物体与水平面间的动摩擦因数μ=0.2,若F作用6s后撤去,撤去F后物体还能向前运动多长时间才停止?(g取10 m/s2) 用动量定理分别从分段及全程两个角度进行求解.
二、动量定理的应用
用动量定理处理多过程问题
[例题1]一现代仿制的地动仪,龙口中的铜珠到蟾蜍口的距离为h,当感知到地震时,质量为m的铜珠(初速度为零)离开龙口,落入蟾蜍口中,与蟾蜍口碰撞的时间约为t,重力加速度为g,不计空气阻力,则铜珠对蟾蜍口产生的冲击力大小约为( )
二、动量定理的应用
用动量定理处理多过程问题
[例题2]某消防队员从一平台上跳下,下落1s后双脚触地,接着他用双腿弯曲的方法缓冲,使自身重心又下降了0.2 s,在着地过程中地面对他双脚的平均作用力约为( )
二、动量定理的应用
用动量定理处理流体问题
(1)建立“柱体”模型.对于流体,可沿流速v的方向选取一段柱形流体,设在Δt时间内通过某一横截面积为S的流体长度 Δl=v·Δt,如图,若流体的密度为ρ,那么在这段时间内流过该截面的流体的质量为 Δm=ρSΔl=ρSvΔt .
(2)运用动量定理,即流体微元所受的合力的冲量等于微元动量的增量,即F合Δt=Δp. (Δt足够短时,重力可忽略不计)
二、动量定理的应用
用动量定理处理流体问题
[例题3]水力采煤时,用水枪在高压下喷出的强力水柱冲击煤层.设水柱直径为d=30 cm,水速为v=50m/s.假设水柱射在煤层的表面上,冲击煤层后水的速度变为零.求水柱对煤层的平均冲击力的大小.(水的密度ρ=1.0×103 kg/m3,结果保留三位有效数字)
二、动量定理的应用
用动量定理处理流体问题
[例题4]假如有一宇宙飞船,它的正面面积为S=0.98 m2,以v=2×103 m/s的速度进入宇宙微粒尘区,尘区每1 m3空间有一微粒,每一微粒平均质量m=2×10-4 g,若要使飞船速度保持不变,飞船的牵引力应增加多少?(设微粒与飞船相碰后附着到飞船上)
例题4.一铁块压着一纸条放在水平桌面上,当以速度v抽出纸条后,铁块掉在地上的P点.若以2v速度抽出纸条,则铁块落地点为( )
A.仍在P点
B.在P点左边
C.在P点右边不远处
D.在P点右边原水平位移的两倍处
B
用 解决生活中的实际问题
I = p ′- p
合
二、动量定理的应用
冲量
功
区
别
公式
标矢性
意义
正负
作用效果
单位
某个力对物体有冲量,不一定做功;某个力对物体做了功,一定有冲量。
N·S
I=Ft
W=Fxcos θ
矢量
标量
N·m 或(J)
力对时间的积累, 对应一段时间
在F-t图像中可以用面积表示
力对位移的积累, 对应一段位移
在F-x图像中可以用面积表示
正负表示与正方向相同或相反
正负表示动力做功或阻力做功
改变物体的动量
改变物体的动能
F
t
O
F
t
x
F
O
F
x
三、冲量与功
1.如图,一物体静止在水平地面上,受到与水平方向成θ角的恒定拉力F作用时间t后,物体仍保持静止。以下看法种正确的是( )
四、练习与应用
教材 第10页
A.物体所受拉力F的冲量方向水平向右
B.物体所受拉力F的冲量大小是Ftcos θ
C.物体所受摩擦力的冲量大小为0
D.物体所受合力的冲量大小为0
2.如图,体操运动员在落地时总要屈腿,这是为什么?
四、练习与应用
教材 第10页
3.如图,用0.5 kg的铁锤钉钉子,打击前铁锤的速度为4m/s。打击后铁锤的速度变为0,设打击时间为0.01s。
(1)不计铁锤所受的重力,铁锤钉钉子的平均作用力是多大?
(2)考虑铁锤所受的重力,铁锤钉钉子的平均作用力是多大?
(3)你分析一下,在计算铁锤钉钉子的平均作用力时,
在什么情况下可以不计铁锤所受的重力。
四、练习与应用
教材 第10页
4.一个质量为10kg的物体,以10m/s的速度做直线运动,受到一个反向的作用力F,经过4s,速度变为反向2m/s。这个力是多大?
四、练习与应用
教材 第10页
5.一个质量为60kg的蹦床运动员,从离水平网面3.2m高处自由下落,着网后沿竖直方向蹦回到离水平网面5.0m高处。已知运动员与网接触的时间为0.8s,g取10m/s2。
(1)求运动员与网接触的这段时间内动量的变化量;
(2)求网对运动员的平均作用力大小;
(3)求从自由下落开始到蹦回离水平网面5.0 m高处这一过程中运动员所受重力冲量、弹力冲量。
四、练习与应用
教材 第10页
6.曾经有一则新闻报道,一名4岁儿童从3层高的楼房掉下来,被一名见义勇为的青年接住。请你估算一下,儿童受到的合力的冲量是多大?设儿童与青年之间的相互作用时间为0.1s,则儿童受到的合力的平均值有多大?
四、练习与应用
教材 第10页
