【新课标】6.4.2多边形外角和 课件(共19张PPT)
文档属性
| 名称 | 【新课标】6.4.2多边形外角和 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-25 14:47:55 | ||
图片预览






文档简介
(共19张PPT)
6.4.2多边形外角和
北师版八年级下册
教学目标
1.经历探索多边形外角和公式的过程,进一步发展合情推理能力。
2. 掌握多边形外角和公式,进一步发展演绎推理能力。
新知导入
1、多边形的内角和公式是什么
2、正n边形的内角怎么计算?
(n-2)·180°
新知讲解
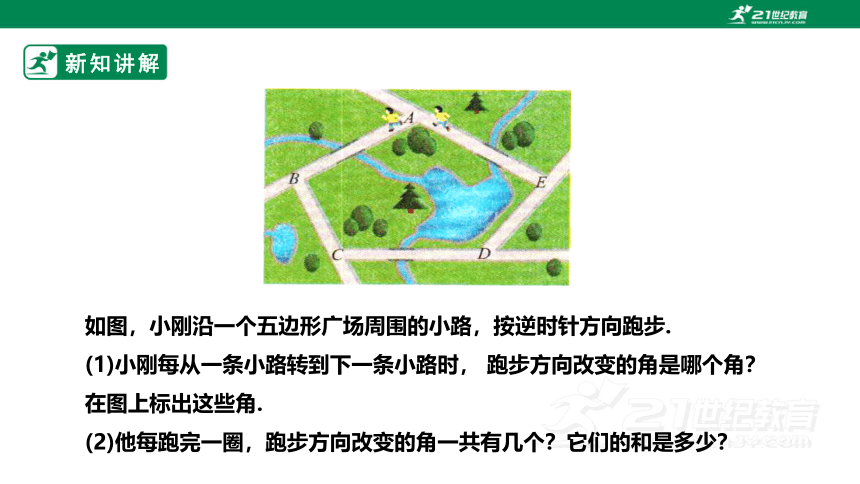
如图,小刚沿一个五边形广场周围的小路,按逆时针方向跑步.
(1)小刚每从一条小路转到下一条小路时, 跑步方向改变的角是哪个角?在图上标出这些角.
(2)他每跑完一圈,跑步方向改变的角一共有几个?它们的和是多少?
新知讲解
小刚是这样思考的:如图,
跑步方向改变的角分别是∠l,
∠2,∠3,∠4,∠5.
∵∠1+∠EAB=180°,
∠2+∠ABC=180°,
∠3+∠BCD=180°,
∠4+∠CDE=180°,
∠5+∠DEA=180°,
新知讲解
∴∠1+∠EAB+∠2+∠ABC +∠3+∠BCD +∠4+∠CDE +∠5+∠DEA=900°.
∵五边形的内角和为(5-2)×180°=540°,
即 ∠EAB+∠ABC+∠BCD+∠CDE+∠DEA=540°.
∴∠1+∠2+∠3+∠4+∠5=900°-540°=360°.
你的思路与小刚一样吗?与同伴交流.
想一想
如果广场的形状是六边形、八边形,那么结果会怎样?
1.多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角,在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
2.定理:多边形的外角和都等于360°.
典例精析
例2 一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和是
(n-2)·180°,外角和等于360°,
所以(n-2)·180 °=3×360 °
解得:n=8
答:这个多边形是八边形.
知识要点
(1)用多边形外角和定理求内(外)角或求正多边形的边数,一般可利用方程思想,通过列方程解决,都是列出外角和的字母表达式:各个外角的和(如本例)或边数×正多边形每个外角的度数,再说明它们等于360°,即可求出;
(2)由于多边形的外角和等于360°,因此有些正多边形的内角问题也可以转化为外角问题来解决.
练一练
如图,小亮从A点出发,沿直线前进10 m后向左转30°,再沿直线前进10 m,又向左转30°……照这样走下去,小亮第一次回到出发地A点时,他一共走了________.
360°÷30°=12
12×10=120m
120m
归纳总结
多边形的内(外)角和与边数间的关系:
(1)多边形的内角与边数有关,且随着边数的增加而增加.
(2)多边形的外角和恒等于360°,与边数的多少无关,其作用是:
①已知正多边形外角的度数,求正多边形的边数;
②已知正多边形的边数,求各相等外角的度数.
课堂练习
1.一个正多边形的内角和是540゜,则这个正多边形的每一个外角等于( ).
A.60゜ B.72゜ C.90゜ D.108゜
2.一个多边形的内角和与外角和的和为540°,则它是( )
A.五边形 B.四边形
C.三角形 D.不能确定
B
C
课堂练习
3.已知正多边形的一个外角为40°,则这个正多边形的内角和为 。
4.如图,△ABC的三边所在的直线与直线分别两两相交,则
∠∠= .
1260°
360°
课堂练习
5.有一个正多边形,它的一个外角等于相邻内角的0.2倍,这个多边形是几边形?
解:设这个正多边形的每个内角为x°,
则每个外角为0.2x°,
得x°+0.2x°=180°,
解得x°=150°,
则0.2x°=0.2×150°=30°.
这个正多边形的边数为:360°÷30°=12.
因此,这个多边形是十二边形.
课堂总结
1.多边形的内角和等于(n-2)·180°,多边形的外角和等于360°.
2.多边形的边数与内角和、外角和的关系:
(1)n边形的内角和等于(n-2)·180°(n≥3,n是正整数),可见多边形内角和与边数n有关,每增加1条边,内角和增加180°.
(2)多边形的外角和等于360°,与边数的多少无关.
3.正n边形:正n边形的内角的度数为,外角的度数为
板书设计
课题:6.4.2多边形外角和
1.外角的定义
2.多边形外角和是360°
作业布置
【必做题】
教材157页练习题1、2、3题
【选做题】
教材157页练习题4题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
6.4.2多边形外角和
北师版八年级下册
教学目标
1.经历探索多边形外角和公式的过程,进一步发展合情推理能力。
2. 掌握多边形外角和公式,进一步发展演绎推理能力。
新知导入
1、多边形的内角和公式是什么
2、正n边形的内角怎么计算?
(n-2)·180°
新知讲解
如图,小刚沿一个五边形广场周围的小路,按逆时针方向跑步.
(1)小刚每从一条小路转到下一条小路时, 跑步方向改变的角是哪个角?在图上标出这些角.
(2)他每跑完一圈,跑步方向改变的角一共有几个?它们的和是多少?
新知讲解
小刚是这样思考的:如图,
跑步方向改变的角分别是∠l,
∠2,∠3,∠4,∠5.
∵∠1+∠EAB=180°,
∠2+∠ABC=180°,
∠3+∠BCD=180°,
∠4+∠CDE=180°,
∠5+∠DEA=180°,
新知讲解
∴∠1+∠EAB+∠2+∠ABC +∠3+∠BCD +∠4+∠CDE +∠5+∠DEA=900°.
∵五边形的内角和为(5-2)×180°=540°,
即 ∠EAB+∠ABC+∠BCD+∠CDE+∠DEA=540°.
∴∠1+∠2+∠3+∠4+∠5=900°-540°=360°.
你的思路与小刚一样吗?与同伴交流.
想一想
如果广场的形状是六边形、八边形,那么结果会怎样?
1.多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角,在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
2.定理:多边形的外角和都等于360°.
典例精析
例2 一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和是
(n-2)·180°,外角和等于360°,
所以(n-2)·180 °=3×360 °
解得:n=8
答:这个多边形是八边形.
知识要点
(1)用多边形外角和定理求内(外)角或求正多边形的边数,一般可利用方程思想,通过列方程解决,都是列出外角和的字母表达式:各个外角的和(如本例)或边数×正多边形每个外角的度数,再说明它们等于360°,即可求出;
(2)由于多边形的外角和等于360°,因此有些正多边形的内角问题也可以转化为外角问题来解决.
练一练
如图,小亮从A点出发,沿直线前进10 m后向左转30°,再沿直线前进10 m,又向左转30°……照这样走下去,小亮第一次回到出发地A点时,他一共走了________.
360°÷30°=12
12×10=120m
120m
归纳总结
多边形的内(外)角和与边数间的关系:
(1)多边形的内角与边数有关,且随着边数的增加而增加.
(2)多边形的外角和恒等于360°,与边数的多少无关,其作用是:
①已知正多边形外角的度数,求正多边形的边数;
②已知正多边形的边数,求各相等外角的度数.
课堂练习
1.一个正多边形的内角和是540゜,则这个正多边形的每一个外角等于( ).
A.60゜ B.72゜ C.90゜ D.108゜
2.一个多边形的内角和与外角和的和为540°,则它是( )
A.五边形 B.四边形
C.三角形 D.不能确定
B
C
课堂练习
3.已知正多边形的一个外角为40°,则这个正多边形的内角和为 。
4.如图,△ABC的三边所在的直线与直线分别两两相交,则
∠∠= .
1260°
360°
课堂练习
5.有一个正多边形,它的一个外角等于相邻内角的0.2倍,这个多边形是几边形?
解:设这个正多边形的每个内角为x°,
则每个外角为0.2x°,
得x°+0.2x°=180°,
解得x°=150°,
则0.2x°=0.2×150°=30°.
这个正多边形的边数为:360°÷30°=12.
因此,这个多边形是十二边形.
课堂总结
1.多边形的内角和等于(n-2)·180°,多边形的外角和等于360°.
2.多边形的边数与内角和、外角和的关系:
(1)n边形的内角和等于(n-2)·180°(n≥3,n是正整数),可见多边形内角和与边数n有关,每增加1条边,内角和增加180°.
(2)多边形的外角和等于360°,与边数的多少无关.
3.正n边形:正n边形的内角的度数为,外角的度数为
板书设计
课题:6.4.2多边形外角和
1.外角的定义
2.多边形外角和是360°
作业布置
【必做题】
教材157页练习题1、2、3题
【选做题】
教材157页练习题4题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
