期末易错专题:三角形、平行四边形和梯形(单元测试) 小学数学四年级下册苏教版(含答案)
文档属性
| 名称 | 期末易错专题:三角形、平行四边形和梯形(单元测试) 小学数学四年级下册苏教版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-26 11:04:28 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末易错专题:三角形、平行四边形和梯形(单元测试)-小学数学四年级下册苏教版
一、选择题
1.等边三角形也是( )三角形。
A.锐角 B.直角 C.钝角
2.三角形的两条边长都是16厘米,那么第三条边长一定( )32厘米。
A.大于 B.等于 C.小于
3.下面( )组小棒不能围成三角形。
A. B.
C.
4.下面的木框架中,( )最稳固。
A. B. C.
5.将一个大的等腰直角三角形平均分成两个小三角形,其中一个小三角形的内角和是( )度。
A.90 B.180 C.360
6.下图中,共有( )个平行四边形。
A.4 B.6 C.9
二、填空题
7.常见的四边形有( )、( )、( )、( )等,其中长方形和正方形是特殊的( )。判断平行四边形的标准是看两组对边是否( ),判断梯形的标准是必须是四边形并且只有( )组对边平行。
8.一个三角形中,最多只能有( )个钝角,( )个直角,( )个锐角。
9.对三角形进行分类,并说说你的分类方法。
分析与解答:
(1)我们观察这些三角形的角,发现有些三角形的三个角都是锐角,这类三角形就是( )三角形;有些三角形有一个直角,这类三角形就是( )三角形;有些三角形有一个钝角,这类三角形就是( )三角形。
(2)我们观察这些三角形的边,发现有些三角形的三条边都相等,这类三角形就是( )三角形;有些三角形的两条边相等,这类三角形就是( )三角形。
10.如下图,一个四边形被遮住了一部分,这个图形可能是( )。
11.如图所示,把一个三角形的三个角撕下来,然后拼在一起,就可以看到∠1,∠2,∠3正好可以组成一个( )角,即( )°。
12.东东用三根铁丝围成一个三角形。他已经剪了两根,分别长5厘米和8厘米,第三根至少要剪( )厘米(填整厘米数)。
三、判断题
13.有一组对边平行的四边形是梯形。( )
14.平行四边形、长方形和梯形的对边互相平行。( )
15.在钝角三角形中,两个锐角之和大于90°。( )
16.如果有一个角是60°,这个三角形一定是等边三角形。( )
17.两个形状相同、大小相等的直角梯形能拼成一个长方形。( )
四、作图题
18.在点子图上按要求画图形。
五、解答题
19.用3根分别长10厘米、20厘米、30厘米的小棒能摆成一个三角形吗?
20.一个等边三角形的边长是5厘米,它的周长是多少厘米?
21.用30厘米长的绳子围成一个等腰三角形,它的一条腰长是12厘米,那么它的底边长多少厘米?
22.用一根217厘米长的铁丝正好围成一个等腰梯形。梯形的上底是31厘米,下底是66厘米,它的一条腰长多少厘米?
23.三角形ABC中,∠A=80°,∠B=30°,∠C=?它是什么三角形?
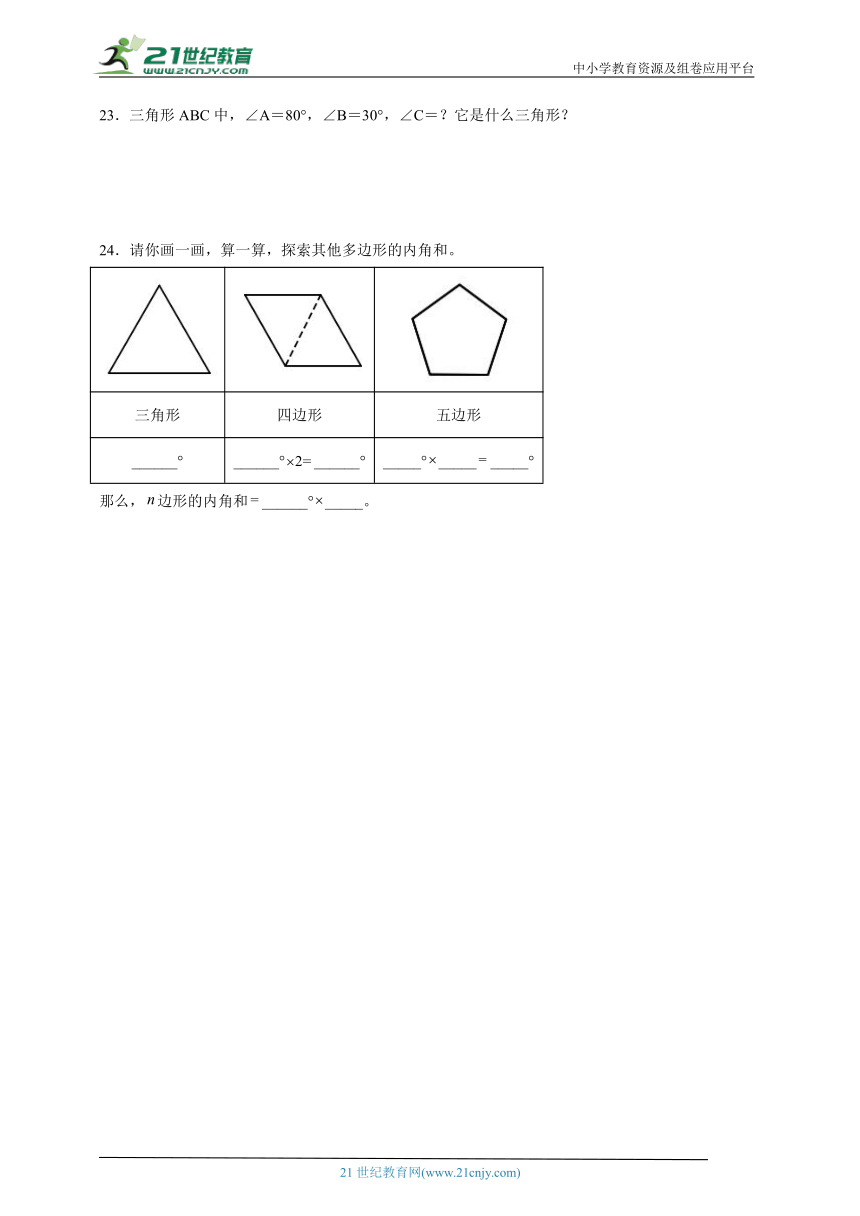
24.请你画一画,算一算,探索其他多边形的内角和。
三角形 四边形 五边形
______° ______°______° _____°__________°
那么,边形的内角和______°_____。
参考答案:
1.A
【分析】等边三角形三条边相等,三个角也相等,都是60°,三个角都是锐角的三角形是锐角三角形。
【详解】等边三角形也是锐角三角形。
故答案为:A
【点睛】熟记等边三角形特征是解题关键。
2.C
【分析】三角形三条边的关系为:在一个三角形中,任意两条边的和大于第三边,任意两条边的差小于第三边。
【详解】因为三角形的两条边长都是16厘米,16+16=32(厘米),大于第三边,所以第三条边长一定小于32厘米。
故答案为:C
【点睛】明确三角形的三边关系是解答此题的关键。
3.C
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】A.3+3>3,则长3、3、3的三根小棒能组成三角形;
B.3+4>5,则长3、4、5的三根小棒能组成三角形;
C.2+2<6,则长2、2、6的三根小棒不能组成三角形。
故答案为:C
【点睛】熟练掌握三角形的三边关系,灵活运用三角形的三边关系解决问题。
4.B
【分析】平行四边形易变形,具有不稳定性;三角形不易变形,具有稳定性;据此即可解答。
【详解】A.图形是由长方形组成,易变形,不稳固。
B.图形是由三角形组成,不易变形,很稳固。
C.图形是由长方形组成,易变形,不稳固。
故答案为:B
【点睛】本题主要考查学生对三角形和平行四边特点的掌握和灵活运用。
5.B
【分析】分成的两个三角形小一些,但还是三角形,只要是三角形内角和都是180度。
【详解】每个小三角形的内角和同样是180度。
故答案为:B
【点睛】考查学生对三角形内角和的理解。
6.C
【分析】单个小平行四边形有4个,由两个小平行四边形组成的平行四边形有4个,由四个小平行四边形组成的平行四边形有1个,共有(4+4+1=9)个平行四边形,据此即可解答。
【详解】根据分析可知,
4+4+1=9(个)
图中共有9个平行四边形。
故答案为:C
【点睛】本题主要考查学生对平行四边形的认识,按一定规律来数,这可以避免漏数或数重。
7. 长方形 正方形 平行四边形 梯形 平行四边形 平行 一
【分析】平行四边形的两组对边平行,梯形只有一组对边平行。长方形的两组对边平行,有4个直角。正方形的两组对边平行,有4个直角,4条边相等。则正方形是特殊的长方形,正方形和长方形是特殊的平行四边形,据此解答。
【详解】常见的四边形有长方形、正方形、平行四边形、梯形等,其中长方形和正方形是特殊的平行四边形。判断平行四边形的标准是看两组对边是否平行,判断梯形的标准是必须是四边形并且只有一组对边平行。
【点睛】本题考查四边形的分类及关系,关键是实际各个图形的特特征。
8. 1 1 3
【分析】根据三角形的内角和为180°可知,三角形中最多有一个直角或钝角,至少有2个锐角,最多有3个锐角。这是因为若三角形中有两个、三个直角或钝角,这个三角形的内角和大于180°,这与三角形的内角和定理相悖。据此解答。
【详解】由分析得:
一个三角形中,最多只能有1个钝角,1个直角,3个锐角。
【点睛】本题考查三角形内角和定理的灵活应用,需熟练掌握。
9.(1) 锐角 直角 钝角
(2) 等边 等腰
【详解】(1)我们观察这些三角形的角,发现有些三角形的三个角都是锐角,这类三角形就是锐角三角形(例图③④⑤);有些三角形有一个直角,这类三角形就是直角三角形(例图①②);有些三角形有一个钝角,这类三角形就是钝角三角形(例图⑥⑦⑧⑨)。
(2)我们观察这些三角形的边,发现有些三角形的三条边都相等,这类三角形就是等边三角形(例图③④⑤);有些三角形的两条边相等,这类三角形就是等腰三角形(例图②)。
10.梯形
【分析】两组对边分别平行且相等的四边形叫做平行四边形;只有一组对边平行的四边形叫做梯形;长方形的对边分别平行且相等,四个角都是直角;正方形四条边都相等,四个角都是直角。从四边形露出部分可以看出,这个四边形有一个角不是直角,这个四边形不可能是长方形或正方形,这个四边形露出的对边不平行,不可能是平行四边形,这个四边形可能是梯形。
【详解】如下图,一个四边形被遮住了一部分,这个图形可能是(梯形)。
【点睛】熟记常见四边形的特征是解题关键。
11. 平 180
【分析】把一个三角形的三个角撕下来,然后拼在一起,三个角的度数和就是三角形的内角和。三角形的内角和等于180°。
【详解】如图所示,把一个三角形的三个角撕下来,然后拼在一起,就可以看到∠1,∠2,∠3正好可以组成一个(平)角,即(180)°。
【点睛】此题考查的是三角形的内角和的探索。
12.4
【分析】三角形任意两边之和大于第三边,任意两边之差小于第三边,据此即可解答。
【详解】5+8=13(厘米)
8-5=3(厘米)
13厘米>第三根铁丝>3厘米
所以第三根铁丝至少要剪4厘米。
【点睛】本题主要考查学生对三角形三边关系的掌握。
13.×
【分析】根据梯形的含义:只有一组对边平行的四边形叫梯形,进行判断即可。
【详解】四边形的一组对边平行,若另一组对边不平行,这个四边形是梯形。若另一组对边平行,这个四边形是平行四边形。
故答案为:×
【点睛】熟练掌握梯形的概念是解题的关键。
14.×
【分析】两组对边分别平行且相等的四边形叫做平行四边形;只有一组对边平行的四边形叫做梯形;长方形的对边分别平行且相等,四个角都是直角。
【详解】平行四边形、长方形对边互相平行,梯形只有一组对边互相平行。
故答案为:×
【点睛】熟记平行四边形、长方形和梯形的特征是解题关键。
15.×
【分析】大于90°小于180°的角叫钝角,有一个角是钝角的三角形是钝角三角形,三角形的内角和是180°,180°减去一个大于90°的角,差小于90°,也就是钝角三角形的两个锐角之和小于90°。
【详解】在钝角三角形中,两个锐角之和小于90°。
故答案为:×
【点睛】熟练掌握钝角三角形的特征和三角形的内角和是180°是解题关键。
16.×
【分析】等边三角形的三个内角都是60°,而这个三角形有一个内角是60°,其余的两个角是不是60°不一定,所以这个三角形未必是等边三角形。
【详解】如果有一个角是60°,这个三角形一定是等边三角形,这句话不对。
故答案为:×
【点睛】考查学生对等边三角形的认识。
17.√
【分析】根据直角梯形的特征:一组对边平行,有两个直角;据此将两个完全一样的直角梯形进行拼组,可以拼成长方形,正方形,等腰梯形或平行四边形,据此解答。
【详解】根据分析可知,两个形状相同、大小相等的直角梯形能拼成一个长方形。
原题干说法正确。
故答案为:√
【点睛】本题考查的是平面图形的认识,关键是了解直角梯形和长方形的特征,进行解答。
18.见详解
【分析】直角三角形:有一个角是直角的三角形;
等腰三角形:有两条边相等的三角形;
梯形:只有一组对边平行的四边形。
【详解】如下图:
(答案不唯一)
【点睛】熟练掌握直角三角形、等腰三角形、梯形的定义是解答此题的关键。
19.不能
【分析】先求出两条较短边的长度之和,再与第三条边的长度比较,发现两边之和等于第三边,不能摆成三角形。
【详解】10+20=30(厘米)
30=30
答:不能摆成三角形。
【点睛】三角形的任意两边之和大于第三边。
20.15厘米
【分析】等边三角形的三条边相等,则等边三角形的周长=边长×3,代入数据计算即可。
【详解】5×3=15(厘米)
答:它的周长是15厘米。
【点睛】本题考查等边三角形的周长,关键是熟记等边三角形的周长公式。
21.6厘米
【分析】根据题意,两条腰长之和为(12+12)厘米,再用30减去两条腰长之和,求出它的底边长多少厘米。
【详解】30-(12+12)
=30-24
=6(厘米)
答:它的底边长6厘米。
【点睛】解答此题的关键是明确等腰三角形的两条腰相等,再进一步解答。
22.60厘米
【分析】等腰梯形的两条腰相等,梯形的周长减去两个底的长度等于两条腰的长度,再除以2即等于一条腰长,据此即可解答。
【详解】(217-31-66)÷2
=120÷2
=60(厘米)
答:它的一条腰长60厘米。
【点睛】本题主要考查学生对梯形的周长和分类知识的掌握。
23.70°;锐角三角形
【分析】因为三角形的内角和是180°,所以用180°减去∠A的度数再去∠B的度数,即可求出第三个角的度数,然后根据三角形的分类进行判断即可。
三角形按边分可分为:等边三角形、等腰三角形、不等边三角形。两个底角相等的三角形是等腰三角形,三个角都相等的三角形是等边三角形。
三角形按角分类可分成:锐角三角形、直角三角形、钝角三角形。
1、锐角三角形:三个角都小于90°。
2、直角三角形:其中一个角等于90°。
3、钝角三角形:其中一个角一定大于90°小于180°。
【详解】∠C=180°-∠A-∠B
三角形ABC中三个角都小于90°,它是锐角三角形。
答:∠C=70°,它是锐角三角形。
【点睛】掌握三角形的内角和是180°及三角形的分类是解题的关键。
24.
三角形 四边形 五边形
__180____° __180____°__360____° __180___°__3_____540___°
180;n-2
【分析】三角形内角和等于180°×(3-2)=180°;四边形可以分成2个三角形,内角和等于180°×(4-2)=360°;五边形可以分成三个三角形,内角和等于180°×(5-2)=540°,……,n边形的内角和等于180°×(n-2)。
【详解】
三角形 四边形 五边形
180° 180°×2=360° 180°×(5-2)=540°
那么,n边形的内角和=180°×(n-2)。
【点睛】熟练掌握掌握多边形内角和知识是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末易错专题:三角形、平行四边形和梯形(单元测试)-小学数学四年级下册苏教版
一、选择题
1.等边三角形也是( )三角形。
A.锐角 B.直角 C.钝角
2.三角形的两条边长都是16厘米,那么第三条边长一定( )32厘米。
A.大于 B.等于 C.小于
3.下面( )组小棒不能围成三角形。
A. B.
C.
4.下面的木框架中,( )最稳固。
A. B. C.
5.将一个大的等腰直角三角形平均分成两个小三角形,其中一个小三角形的内角和是( )度。
A.90 B.180 C.360
6.下图中,共有( )个平行四边形。
A.4 B.6 C.9
二、填空题
7.常见的四边形有( )、( )、( )、( )等,其中长方形和正方形是特殊的( )。判断平行四边形的标准是看两组对边是否( ),判断梯形的标准是必须是四边形并且只有( )组对边平行。
8.一个三角形中,最多只能有( )个钝角,( )个直角,( )个锐角。
9.对三角形进行分类,并说说你的分类方法。
分析与解答:
(1)我们观察这些三角形的角,发现有些三角形的三个角都是锐角,这类三角形就是( )三角形;有些三角形有一个直角,这类三角形就是( )三角形;有些三角形有一个钝角,这类三角形就是( )三角形。
(2)我们观察这些三角形的边,发现有些三角形的三条边都相等,这类三角形就是( )三角形;有些三角形的两条边相等,这类三角形就是( )三角形。
10.如下图,一个四边形被遮住了一部分,这个图形可能是( )。
11.如图所示,把一个三角形的三个角撕下来,然后拼在一起,就可以看到∠1,∠2,∠3正好可以组成一个( )角,即( )°。
12.东东用三根铁丝围成一个三角形。他已经剪了两根,分别长5厘米和8厘米,第三根至少要剪( )厘米(填整厘米数)。
三、判断题
13.有一组对边平行的四边形是梯形。( )
14.平行四边形、长方形和梯形的对边互相平行。( )
15.在钝角三角形中,两个锐角之和大于90°。( )
16.如果有一个角是60°,这个三角形一定是等边三角形。( )
17.两个形状相同、大小相等的直角梯形能拼成一个长方形。( )
四、作图题
18.在点子图上按要求画图形。
五、解答题
19.用3根分别长10厘米、20厘米、30厘米的小棒能摆成一个三角形吗?
20.一个等边三角形的边长是5厘米,它的周长是多少厘米?
21.用30厘米长的绳子围成一个等腰三角形,它的一条腰长是12厘米,那么它的底边长多少厘米?
22.用一根217厘米长的铁丝正好围成一个等腰梯形。梯形的上底是31厘米,下底是66厘米,它的一条腰长多少厘米?
23.三角形ABC中,∠A=80°,∠B=30°,∠C=?它是什么三角形?
24.请你画一画,算一算,探索其他多边形的内角和。
三角形 四边形 五边形
______° ______°______° _____°__________°
那么,边形的内角和______°_____。
参考答案:
1.A
【分析】等边三角形三条边相等,三个角也相等,都是60°,三个角都是锐角的三角形是锐角三角形。
【详解】等边三角形也是锐角三角形。
故答案为:A
【点睛】熟记等边三角形特征是解题关键。
2.C
【分析】三角形三条边的关系为:在一个三角形中,任意两条边的和大于第三边,任意两条边的差小于第三边。
【详解】因为三角形的两条边长都是16厘米,16+16=32(厘米),大于第三边,所以第三条边长一定小于32厘米。
故答案为:C
【点睛】明确三角形的三边关系是解答此题的关键。
3.C
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】A.3+3>3,则长3、3、3的三根小棒能组成三角形;
B.3+4>5,则长3、4、5的三根小棒能组成三角形;
C.2+2<6,则长2、2、6的三根小棒不能组成三角形。
故答案为:C
【点睛】熟练掌握三角形的三边关系,灵活运用三角形的三边关系解决问题。
4.B
【分析】平行四边形易变形,具有不稳定性;三角形不易变形,具有稳定性;据此即可解答。
【详解】A.图形是由长方形组成,易变形,不稳固。
B.图形是由三角形组成,不易变形,很稳固。
C.图形是由长方形组成,易变形,不稳固。
故答案为:B
【点睛】本题主要考查学生对三角形和平行四边特点的掌握和灵活运用。
5.B
【分析】分成的两个三角形小一些,但还是三角形,只要是三角形内角和都是180度。
【详解】每个小三角形的内角和同样是180度。
故答案为:B
【点睛】考查学生对三角形内角和的理解。
6.C
【分析】单个小平行四边形有4个,由两个小平行四边形组成的平行四边形有4个,由四个小平行四边形组成的平行四边形有1个,共有(4+4+1=9)个平行四边形,据此即可解答。
【详解】根据分析可知,
4+4+1=9(个)
图中共有9个平行四边形。
故答案为:C
【点睛】本题主要考查学生对平行四边形的认识,按一定规律来数,这可以避免漏数或数重。
7. 长方形 正方形 平行四边形 梯形 平行四边形 平行 一
【分析】平行四边形的两组对边平行,梯形只有一组对边平行。长方形的两组对边平行,有4个直角。正方形的两组对边平行,有4个直角,4条边相等。则正方形是特殊的长方形,正方形和长方形是特殊的平行四边形,据此解答。
【详解】常见的四边形有长方形、正方形、平行四边形、梯形等,其中长方形和正方形是特殊的平行四边形。判断平行四边形的标准是看两组对边是否平行,判断梯形的标准是必须是四边形并且只有一组对边平行。
【点睛】本题考查四边形的分类及关系,关键是实际各个图形的特特征。
8. 1 1 3
【分析】根据三角形的内角和为180°可知,三角形中最多有一个直角或钝角,至少有2个锐角,最多有3个锐角。这是因为若三角形中有两个、三个直角或钝角,这个三角形的内角和大于180°,这与三角形的内角和定理相悖。据此解答。
【详解】由分析得:
一个三角形中,最多只能有1个钝角,1个直角,3个锐角。
【点睛】本题考查三角形内角和定理的灵活应用,需熟练掌握。
9.(1) 锐角 直角 钝角
(2) 等边 等腰
【详解】(1)我们观察这些三角形的角,发现有些三角形的三个角都是锐角,这类三角形就是锐角三角形(例图③④⑤);有些三角形有一个直角,这类三角形就是直角三角形(例图①②);有些三角形有一个钝角,这类三角形就是钝角三角形(例图⑥⑦⑧⑨)。
(2)我们观察这些三角形的边,发现有些三角形的三条边都相等,这类三角形就是等边三角形(例图③④⑤);有些三角形的两条边相等,这类三角形就是等腰三角形(例图②)。
10.梯形
【分析】两组对边分别平行且相等的四边形叫做平行四边形;只有一组对边平行的四边形叫做梯形;长方形的对边分别平行且相等,四个角都是直角;正方形四条边都相等,四个角都是直角。从四边形露出部分可以看出,这个四边形有一个角不是直角,这个四边形不可能是长方形或正方形,这个四边形露出的对边不平行,不可能是平行四边形,这个四边形可能是梯形。
【详解】如下图,一个四边形被遮住了一部分,这个图形可能是(梯形)。
【点睛】熟记常见四边形的特征是解题关键。
11. 平 180
【分析】把一个三角形的三个角撕下来,然后拼在一起,三个角的度数和就是三角形的内角和。三角形的内角和等于180°。
【详解】如图所示,把一个三角形的三个角撕下来,然后拼在一起,就可以看到∠1,∠2,∠3正好可以组成一个(平)角,即(180)°。
【点睛】此题考查的是三角形的内角和的探索。
12.4
【分析】三角形任意两边之和大于第三边,任意两边之差小于第三边,据此即可解答。
【详解】5+8=13(厘米)
8-5=3(厘米)
13厘米>第三根铁丝>3厘米
所以第三根铁丝至少要剪4厘米。
【点睛】本题主要考查学生对三角形三边关系的掌握。
13.×
【分析】根据梯形的含义:只有一组对边平行的四边形叫梯形,进行判断即可。
【详解】四边形的一组对边平行,若另一组对边不平行,这个四边形是梯形。若另一组对边平行,这个四边形是平行四边形。
故答案为:×
【点睛】熟练掌握梯形的概念是解题的关键。
14.×
【分析】两组对边分别平行且相等的四边形叫做平行四边形;只有一组对边平行的四边形叫做梯形;长方形的对边分别平行且相等,四个角都是直角。
【详解】平行四边形、长方形对边互相平行,梯形只有一组对边互相平行。
故答案为:×
【点睛】熟记平行四边形、长方形和梯形的特征是解题关键。
15.×
【分析】大于90°小于180°的角叫钝角,有一个角是钝角的三角形是钝角三角形,三角形的内角和是180°,180°减去一个大于90°的角,差小于90°,也就是钝角三角形的两个锐角之和小于90°。
【详解】在钝角三角形中,两个锐角之和小于90°。
故答案为:×
【点睛】熟练掌握钝角三角形的特征和三角形的内角和是180°是解题关键。
16.×
【分析】等边三角形的三个内角都是60°,而这个三角形有一个内角是60°,其余的两个角是不是60°不一定,所以这个三角形未必是等边三角形。
【详解】如果有一个角是60°,这个三角形一定是等边三角形,这句话不对。
故答案为:×
【点睛】考查学生对等边三角形的认识。
17.√
【分析】根据直角梯形的特征:一组对边平行,有两个直角;据此将两个完全一样的直角梯形进行拼组,可以拼成长方形,正方形,等腰梯形或平行四边形,据此解答。
【详解】根据分析可知,两个形状相同、大小相等的直角梯形能拼成一个长方形。
原题干说法正确。
故答案为:√
【点睛】本题考查的是平面图形的认识,关键是了解直角梯形和长方形的特征,进行解答。
18.见详解
【分析】直角三角形:有一个角是直角的三角形;
等腰三角形:有两条边相等的三角形;
梯形:只有一组对边平行的四边形。
【详解】如下图:
(答案不唯一)
【点睛】熟练掌握直角三角形、等腰三角形、梯形的定义是解答此题的关键。
19.不能
【分析】先求出两条较短边的长度之和,再与第三条边的长度比较,发现两边之和等于第三边,不能摆成三角形。
【详解】10+20=30(厘米)
30=30
答:不能摆成三角形。
【点睛】三角形的任意两边之和大于第三边。
20.15厘米
【分析】等边三角形的三条边相等,则等边三角形的周长=边长×3,代入数据计算即可。
【详解】5×3=15(厘米)
答:它的周长是15厘米。
【点睛】本题考查等边三角形的周长,关键是熟记等边三角形的周长公式。
21.6厘米
【分析】根据题意,两条腰长之和为(12+12)厘米,再用30减去两条腰长之和,求出它的底边长多少厘米。
【详解】30-(12+12)
=30-24
=6(厘米)
答:它的底边长6厘米。
【点睛】解答此题的关键是明确等腰三角形的两条腰相等,再进一步解答。
22.60厘米
【分析】等腰梯形的两条腰相等,梯形的周长减去两个底的长度等于两条腰的长度,再除以2即等于一条腰长,据此即可解答。
【详解】(217-31-66)÷2
=120÷2
=60(厘米)
答:它的一条腰长60厘米。
【点睛】本题主要考查学生对梯形的周长和分类知识的掌握。
23.70°;锐角三角形
【分析】因为三角形的内角和是180°,所以用180°减去∠A的度数再去∠B的度数,即可求出第三个角的度数,然后根据三角形的分类进行判断即可。
三角形按边分可分为:等边三角形、等腰三角形、不等边三角形。两个底角相等的三角形是等腰三角形,三个角都相等的三角形是等边三角形。
三角形按角分类可分成:锐角三角形、直角三角形、钝角三角形。
1、锐角三角形:三个角都小于90°。
2、直角三角形:其中一个角等于90°。
3、钝角三角形:其中一个角一定大于90°小于180°。
【详解】∠C=180°-∠A-∠B
三角形ABC中三个角都小于90°,它是锐角三角形。
答:∠C=70°,它是锐角三角形。
【点睛】掌握三角形的内角和是180°及三角形的分类是解题的关键。
24.
三角形 四边形 五边形
__180____° __180____°__360____° __180___°__3_____540___°
180;n-2
【分析】三角形内角和等于180°×(3-2)=180°;四边形可以分成2个三角形,内角和等于180°×(4-2)=360°;五边形可以分成三个三角形,内角和等于180°×(5-2)=540°,……,n边形的内角和等于180°×(n-2)。
【详解】
三角形 四边形 五边形
180° 180°×2=360° 180°×(5-2)=540°
那么,n边形的内角和=180°×(n-2)。
【点睛】熟练掌握掌握多边形内角和知识是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
