19.2.3 一次函数与方程、不等式 课时 1 教案
文档属性
| 名称 | 19.2.3 一次函数与方程、不等式 课时 1 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 376.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-25 16:25:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第19章 一次函数 教案
19.2.3 一次函数与方程、不等式
第1课时
教学目标:
通过作函数图象并观察函数图象,从中体一次函数与一元一次方程、一元一次不等式的内在联系.
重点:
一次函数与一元一次方程、一元一次不等式的关系的理解.
难点:
灵活运用一次函数与一元一次方程、一元一次不等式的关系解决问题.
教学流程:
一、导入新知
情境:今天数学王国搞了个家庭Party,各个成员按照自己所在的集合就坐,这时“x+y=3” 来了.它该去哪是呢?
二、新知讲解
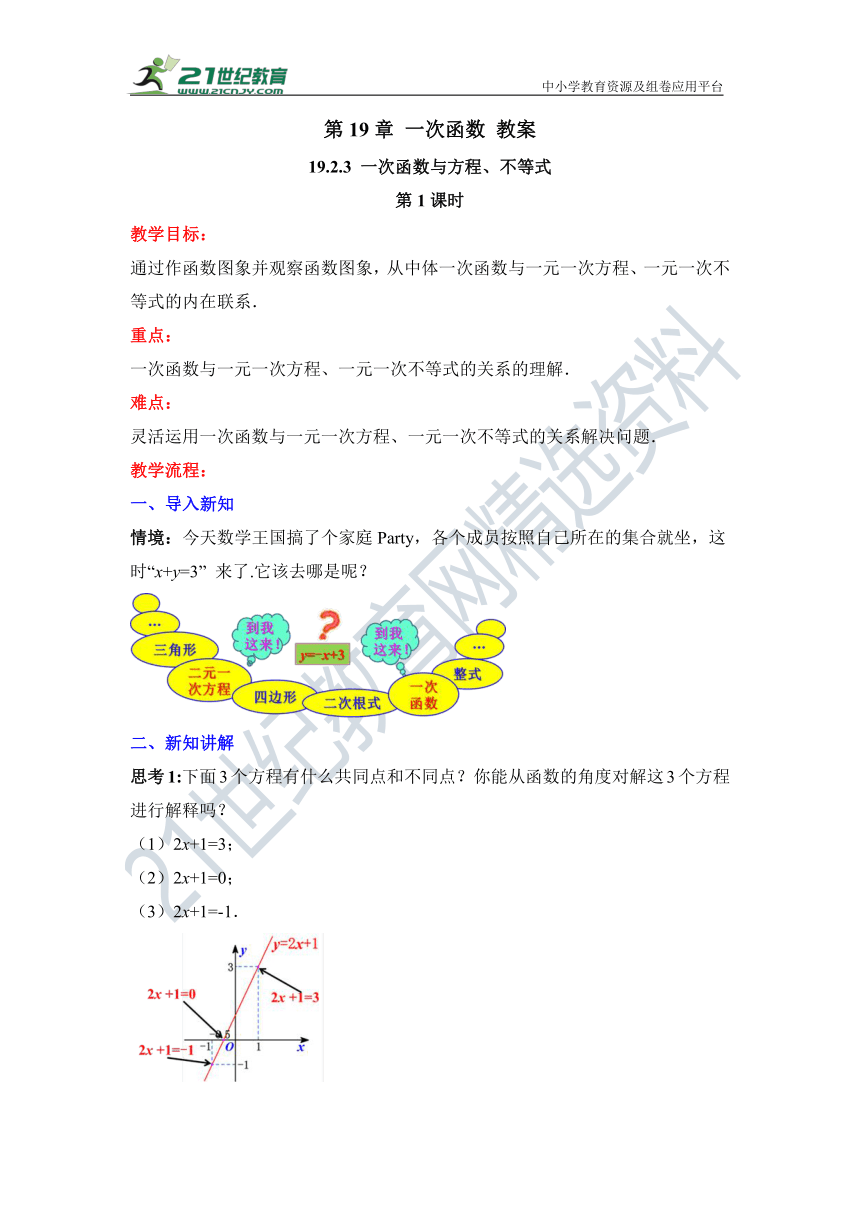
思考1:下面3个方程有什么共同点和不同点?你能从函数的角度对解这3个方程进行解释吗?
(1)2x+1=3;
(2)2x+1=0;
(3)2x+1=-1.
引导1:用函数的观点看:
解一元一次方程kx +b =c 就是求当函数(y=kx +b)值为c时对应的自变量的值.
例1:(1)直线y=x+10与x轴交点坐标为________,这说明方程x+10=0的解是x=_____.
(2)若方程kx+b=0的解是x=6,则直线y=kx+b与x轴交点坐标为__________.
答案:(1)(-10, 0),-10;(2)(6, 0)
归纳1:一次函数与一元一次方程的关系
思考2:下面3个不等式有什么共同点和不同点?你能从函数的角度对解这3个不等式进行解释吗?
(1)3x+2>2;
(2)3x+2<0;
(3)3x+2<-1.
引导2:不等式kx+b>c的解集就是使函数y =kx+b 的函数值大于c的对应的自变量取值范围;
不等式kx+b<c的解集就是使函数y =kx+b 的函数值小于c的对应的自变量取值范围.
例2:画出函数y=-3x+6的图象,结合图象求:
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3
解:函数y=-3x+6的图象如图所示,图象与x轴交于点B(2,0).
(1)由图象可知,不等式-3x+6>0 的解集是图象位于 x轴上方的x的取值范围,即x<2;
不等式 -3x+6<0的解集是图象位于 x轴下方的x的取值范围,即x>2;
(2)由图象可
知,当x>1时,y<3.
归纳2:一次函数与一元一次不等式的关系
三、巩固提升
1.如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )
A.x=2 B.x=0 C.x=-1 D.x=-3
答案:D
2.一元一次方程ax-b=0的解是x=5,则函数y=ax-b的图象与x轴的交点坐标是( )
A.(-5,0) B.(5,0) C.(a,0) D.(-b,0)
答案:B
3.如图,直线y=kx+b交坐标轴于A(-2,0),B(0,3)两点,则不等式kx+b>0的解集是( )
A.x>3 B.-2<x<3 C.x<-2 D.x>-2
答案:D
4.已知一次函数y=kx+b的图象经过两点A(0,1),B(2,0),则当x____时,y≤0.
答案:≥2
5.如图,直线y=kx+b与坐标轴相交于点M(2,0),N(0,4).
(1)求直线MN的解析式;
(2)根据图象,直接写出不等式kx+b≥0的解集.
解: (1)把M,N的坐标代入y=kx+b得,
解得,
∴直线MN的解析式为y=-2x+4.
(2)根据图象可知,不等式kx+b≥0的解集为x≤2.
四、课堂小结
今天我们学习了哪些知识?
1.说一说一次函数与一元一次方程的关系?
2.说一说一次函数与一元一次不等式的关系?
五、布置作业
教材P107页复习题19第5题.
第19章 一次函数 教案
19.2.3 一次函数与方程、不等式
第1课时
教学目标:
通过作函数图象并观察函数图象,从中体一次函数与一元一次方程、一元一次不等式的内在联系.
重点:
一次函数与一元一次方程、一元一次不等式的关系的理解.
难点:
灵活运用一次函数与一元一次方程、一元一次不等式的关系解决问题.
教学流程:
一、导入新知
情境:今天数学王国搞了个家庭Party,各个成员按照自己所在的集合就坐,这时“x+y=3” 来了.它该去哪是呢?
二、新知讲解
思考1:下面3个方程有什么共同点和不同点?你能从函数的角度对解这3个方程进行解释吗?
(1)2x+1=3;
(2)2x+1=0;
(3)2x+1=-1.
引导1:用函数的观点看:
解一元一次方程kx +b =c 就是求当函数(y=kx +b)值为c时对应的自变量的值.
例1:(1)直线y=x+10与x轴交点坐标为________,这说明方程x+10=0的解是x=_____.
(2)若方程kx+b=0的解是x=6,则直线y=kx+b与x轴交点坐标为__________.
答案:(1)(-10, 0),-10;(2)(6, 0)
归纳1:一次函数与一元一次方程的关系
思考2:下面3个不等式有什么共同点和不同点?你能从函数的角度对解这3个不等式进行解释吗?
(1)3x+2>2;
(2)3x+2<0;
(3)3x+2<-1.
引导2:不等式kx+b>c的解集就是使函数y =kx+b 的函数值大于c的对应的自变量取值范围;
不等式kx+b<c的解集就是使函数y =kx+b 的函数值小于c的对应的自变量取值范围.
例2:画出函数y=-3x+6的图象,结合图象求:
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3
解:函数y=-3x+6的图象如图所示,图象与x轴交于点B(2,0).
(1)由图象可知,不等式-3x+6>0 的解集是图象位于 x轴上方的x的取值范围,即x<2;
不等式 -3x+6<0的解集是图象位于 x轴下方的x的取值范围,即x>2;
(2)由图象可
知,当x>1时,y<3.
归纳2:一次函数与一元一次不等式的关系
三、巩固提升
1.如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )
A.x=2 B.x=0 C.x=-1 D.x=-3
答案:D
2.一元一次方程ax-b=0的解是x=5,则函数y=ax-b的图象与x轴的交点坐标是( )
A.(-5,0) B.(5,0) C.(a,0) D.(-b,0)
答案:B
3.如图,直线y=kx+b交坐标轴于A(-2,0),B(0,3)两点,则不等式kx+b>0的解集是( )
A.x>3 B.-2<x<3 C.x<-2 D.x>-2
答案:D
4.已知一次函数y=kx+b的图象经过两点A(0,1),B(2,0),则当x____时,y≤0.
答案:≥2
5.如图,直线y=kx+b与坐标轴相交于点M(2,0),N(0,4).
(1)求直线MN的解析式;
(2)根据图象,直接写出不等式kx+b≥0的解集.
解: (1)把M,N的坐标代入y=kx+b得,
解得,
∴直线MN的解析式为y=-2x+4.
(2)根据图象可知,不等式kx+b≥0的解集为x≤2.
四、课堂小结
今天我们学习了哪些知识?
1.说一说一次函数与一元一次方程的关系?
2.说一说一次函数与一元一次不等式的关系?
五、布置作业
教材P107页复习题19第5题.
