3.4 函数的应用(一)-高中数学人教A版必修一 课件(共23张PPT)
文档属性
| 名称 | 3.4 函数的应用(一)-高中数学人教A版必修一 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 898.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-25 16:57:01 | ||
图片预览








文档简介
(共23张PPT)
第三章 函数的概念与性质
3.4 函数的应用(一)
学习目标:
1.能够利用给定的函数模型或建立函数模型解决实际问题;
2.经历建立函数模型解决实际问题的过程,提高综合运用数学知识和方法解决实际问题的能力.
重点及难点:
1.建立函数模型解决实际问题;
2. 选择适当的方案和函数模型解决实际问题.
我们学习过的一次函数、二次函数、幂函数等都与现实世界有紧密联系.下面通过一些实例感受它们的广泛应用,体会利用函数模型解决实际问题的过程与方法.
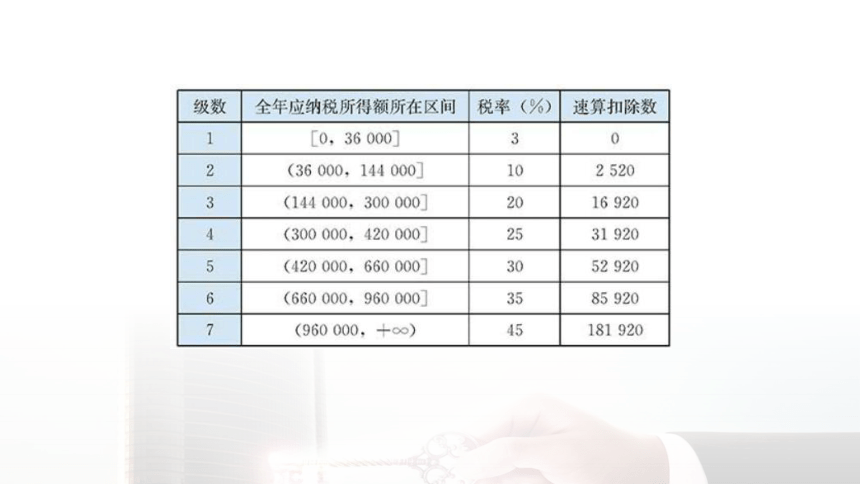
例1. 依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:个税税额=应纳税所得额×税率-速算扣除数.应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.其中,“基本减除费用”(免征额)为每年60 000元.税率与速算扣除数见表.
“综合所得”包括工资、薪金,劳务报酬,稿酬,特许权使用费;“专项扣除”包括居民个人按照国家规定的范围和标准缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金等;“专项附加扣除”包括子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等支出;“其它扣除”是指除上述基本减除费用、专项扣除、专项附加扣除之外,由国务院决定以扣除方式减少纳税的优惠政策规定的费用.
(1)求y关于x的函数关系;
(2)如果全年的综合所得为249 600元,那么他全年应缴纳多少综合所得个税?
设小王全年综合所得收入额为x元,应缴纳综合所得个税税额为y 元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52 800元,依法确定其他扣除是4 560元.
解:根据公式“应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除”及已知得
应纳税所得额 t=x-60000-x(8%+2%+1%+9%)-52800-4560
=0.8x-117360
令0.8x-117360大于0,解得x大于146700,所以
个人应纳税所得额 t 关于综合所得收入额 x 的函数解析式为:
根据“级数”表可知:
当0≤x≤146 700时,t=0,所以y=0;
当146 700所以y=t×3%=0.024x-3520.8;
当191 700所以y=t×10%-2520=0.08x-14256;
当326 700所以y=t×20%-16920=0.16x-40392;
当671 700所以y=t×30%-52920=0.24x-88128;
当971 700所以y=t×35%-85920=0.28x-126996;
当x>1346 700时,t>960 000 ,
所以y=t×45%-181920=0.36x-234732;
当521 700所以y=t×25%-31920=0.2x-61260;
所以,函数解析式为
当x=249600时,y=0.08×249600-14256=5712.
所以,小王全年需要缴纳的综合所得个税税额为5712元.
方法总结
第1步:分析、联想、转化、抽象;
第2步:建立函数模型,把实际应用问题转化为数学问题;
第3步:解答数学问题,求得结果;
第4步:把数学结果转译成具体问题的结论,做出解答.
这四步中,最为关键的是把第2步处理好.只要把函数模型建立妥当,所有的 问题即可在此基础上迎刃而解.
解答函数实际应用问题时,一般要怎么进行
例2.一辆汽车在某段路程中行驶的平均速率v(单位:km/h)与时间t(单位:h)关系如图所示.
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
(2)假设这辆汽车的里程表在汽车行驶这段路程
前的读数为2004km,试建立行驶这段路程时汽车
里程表读数s(单位:km)与时间t的函数解析式,并
画出相应的图象.
分析:当时间 t 在[0,5]内变化时,对于任意的时刻 t 都有唯一确定的行驶路程与之相对应.根据图所示,在时间段[0,1),[1,2),[2,3),[3,4),[4,5]内行驶的平均速率分别为50 km/h, 80 km/h, 90 km/h, 75 km/h, 65 km/h,因此在每个时间段内,行驶路程与时间的关系也不一样,需要分段表述.
解:(1) 阴影部分的面积为
50×1+80×1+90×1+75×1+65×1=360.
阴影部分的面积表示汽车在这5 h内行驶
的路程为360 km.
(2) 根据已知图象,有
总结:本题的解答过程表明,函数图象对分析和理解题意很有帮助.因此,我们要注意提高读图能力.另外,本题用到了分段函数,解决现实问题时经常会用到这类函数.
O
t
s
1
2
3
4
5
2000
2100
2400
2300
2200
1.分段函数的“段”一定要分得合理,不重不漏.
2.分段函数的定义域为对应每一段自变量取值范围的并集.
3.分段函数的值域求法:逐段求函数值的范围,最后比较再下结论.
4.分段函数的最值求法:逐段求函数的最值,最后比较找出最大和最小,再下结论.
总结升华
例3.某水果批发商销售每箱进价为40元的苹果,假设每箱售价不得低于50元且不得高于55元.市场调查发现,若每箱以50元的价格销售,平均每天销售90箱.价格每提高1元,平均每天少销售3箱.
①求平均每天的销售量y(箱)与销售单价x(元/箱)之间的函数关系式;
②求该批发商平均每天的销售利润w(元)与销售单价x(元/箱)之间的函数关系式;
③当每箱苹果的售价为多少元时,可以获得最大利润 最大利润是多少
解:①根据题意,得y=90-3(x-50),
化简,得y=-3x+240(50≤x≤55,x∈N).
②因为该批发商平均每天的销售利润=平均每天的销售量×每箱销售利润.
所以w=(x-40)(-3x+240)=-3x2+360x-9600 (50≤x≤55,x∈N).
③因为w=-3x2+360x-9600=-3(x-60)2+1 200,所以当x<60时,w随x的增大而增大.
又50≤x≤55,x∈N,所以当x=55时,w有最大值,最大值为1125.
所以当每箱苹果的售价为55元时,可以获得最大利润,且最大利润为1125元.
1.某自行车存车处在某一天总共存放车辆4000辆次,存车费为:电动自行车0.3元/辆,普通自行车0.2元/辆.若该天普通自行车存车x辆次,存车费总收入为y元,则y与x的函数关系式为( )
A.y=0.2x(0≤x≤4000) B.y=0.5x(0≤x≤4000)
C.y=-0.1x+1200(0≤x≤4000) D.y=0.1x+12000≤x≤4000)
C
巩固练习
2.某物体一天内的温度T是时间t的函数T(t)=t3-3t+60,时间单位是h,温度单位为℃,t=0时表示中午12:00,则上午8:00时的温度为 ℃.
8
3.商店出售茶壶和茶杯,茶壶定价为每个20元,茶杯每个5元,该商店推出两种优惠办法:
①买一个茶壶赠一个茶杯;
②按总价的92%付款.
某顾客需购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯x(个),付款y(元),试分别建立两种优惠办法中y与x之间的函数解析式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更优惠
解:由优惠办法①可得函数解析式为y1=20×4+5(x-4)=5x+60(x≥4,且x∈N).
由优惠办法②可得y2=(5x+20×4)×92%=4.6x+73.6(x≥4,且x∈N).
y1-y2=0.4x-13.6(x≥4,且x∈N),
令y1-y2=0,得x=34.
所以,当购买34个茶杯时,两种优惠办法付款相同;
当4≤x<34时,y1当x>34时,y1>y2,优惠办法②更省钱.
课堂小结
第1步:分析、联想、转化、抽象;
第2步:建立函数模型,把实际应用问题转化为数学问题;
第3步:解答数学问题,求得结果;
第4步:把数学结果转译成具体问题的结论,做出解答.
解答函数实际应用问题的步骤:
第三章 函数的概念与性质
3.4 函数的应用(一)
学习目标:
1.能够利用给定的函数模型或建立函数模型解决实际问题;
2.经历建立函数模型解决实际问题的过程,提高综合运用数学知识和方法解决实际问题的能力.
重点及难点:
1.建立函数模型解决实际问题;
2. 选择适当的方案和函数模型解决实际问题.
我们学习过的一次函数、二次函数、幂函数等都与现实世界有紧密联系.下面通过一些实例感受它们的广泛应用,体会利用函数模型解决实际问题的过程与方法.
例1. 依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:个税税额=应纳税所得额×税率-速算扣除数.应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.其中,“基本减除费用”(免征额)为每年60 000元.税率与速算扣除数见表.
“综合所得”包括工资、薪金,劳务报酬,稿酬,特许权使用费;“专项扣除”包括居民个人按照国家规定的范围和标准缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金等;“专项附加扣除”包括子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等支出;“其它扣除”是指除上述基本减除费用、专项扣除、专项附加扣除之外,由国务院决定以扣除方式减少纳税的优惠政策规定的费用.
(1)求y关于x的函数关系;
(2)如果全年的综合所得为249 600元,那么他全年应缴纳多少综合所得个税?
设小王全年综合所得收入额为x元,应缴纳综合所得个税税额为y 元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52 800元,依法确定其他扣除是4 560元.
解:根据公式“应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除”及已知得
应纳税所得额 t=x-60000-x(8%+2%+1%+9%)-52800-4560
=0.8x-117360
令0.8x-117360大于0,解得x大于146700,所以
个人应纳税所得额 t 关于综合所得收入额 x 的函数解析式为:
根据“级数”表可知:
当0≤x≤146 700时,t=0,所以y=0;
当146 700
当191 700
当326 700
当671 700
当971 700
当x>1346 700时,t>960 000 ,
所以y=t×45%-181920=0.36x-234732;
当521 700
所以,函数解析式为
当x=249600时,y=0.08×249600-14256=5712.
所以,小王全年需要缴纳的综合所得个税税额为5712元.
方法总结
第1步:分析、联想、转化、抽象;
第2步:建立函数模型,把实际应用问题转化为数学问题;
第3步:解答数学问题,求得结果;
第4步:把数学结果转译成具体问题的结论,做出解答.
这四步中,最为关键的是把第2步处理好.只要把函数模型建立妥当,所有的 问题即可在此基础上迎刃而解.
解答函数实际应用问题时,一般要怎么进行
例2.一辆汽车在某段路程中行驶的平均速率v(单位:km/h)与时间t(单位:h)关系如图所示.
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
(2)假设这辆汽车的里程表在汽车行驶这段路程
前的读数为2004km,试建立行驶这段路程时汽车
里程表读数s(单位:km)与时间t的函数解析式,并
画出相应的图象.
分析:当时间 t 在[0,5]内变化时,对于任意的时刻 t 都有唯一确定的行驶路程与之相对应.根据图所示,在时间段[0,1),[1,2),[2,3),[3,4),[4,5]内行驶的平均速率分别为50 km/h, 80 km/h, 90 km/h, 75 km/h, 65 km/h,因此在每个时间段内,行驶路程与时间的关系也不一样,需要分段表述.
解:(1) 阴影部分的面积为
50×1+80×1+90×1+75×1+65×1=360.
阴影部分的面积表示汽车在这5 h内行驶
的路程为360 km.
(2) 根据已知图象,有
总结:本题的解答过程表明,函数图象对分析和理解题意很有帮助.因此,我们要注意提高读图能力.另外,本题用到了分段函数,解决现实问题时经常会用到这类函数.
O
t
s
1
2
3
4
5
2000
2100
2400
2300
2200
1.分段函数的“段”一定要分得合理,不重不漏.
2.分段函数的定义域为对应每一段自变量取值范围的并集.
3.分段函数的值域求法:逐段求函数值的范围,最后比较再下结论.
4.分段函数的最值求法:逐段求函数的最值,最后比较找出最大和最小,再下结论.
总结升华
例3.某水果批发商销售每箱进价为40元的苹果,假设每箱售价不得低于50元且不得高于55元.市场调查发现,若每箱以50元的价格销售,平均每天销售90箱.价格每提高1元,平均每天少销售3箱.
①求平均每天的销售量y(箱)与销售单价x(元/箱)之间的函数关系式;
②求该批发商平均每天的销售利润w(元)与销售单价x(元/箱)之间的函数关系式;
③当每箱苹果的售价为多少元时,可以获得最大利润 最大利润是多少
解:①根据题意,得y=90-3(x-50),
化简,得y=-3x+240(50≤x≤55,x∈N).
②因为该批发商平均每天的销售利润=平均每天的销售量×每箱销售利润.
所以w=(x-40)(-3x+240)=-3x2+360x-9600 (50≤x≤55,x∈N).
③因为w=-3x2+360x-9600=-3(x-60)2+1 200,所以当x<60时,w随x的增大而增大.
又50≤x≤55,x∈N,所以当x=55时,w有最大值,最大值为1125.
所以当每箱苹果的售价为55元时,可以获得最大利润,且最大利润为1125元.
1.某自行车存车处在某一天总共存放车辆4000辆次,存车费为:电动自行车0.3元/辆,普通自行车0.2元/辆.若该天普通自行车存车x辆次,存车费总收入为y元,则y与x的函数关系式为( )
A.y=0.2x(0≤x≤4000) B.y=0.5x(0≤x≤4000)
C.y=-0.1x+1200(0≤x≤4000) D.y=0.1x+12000≤x≤4000)
C
巩固练习
2.某物体一天内的温度T是时间t的函数T(t)=t3-3t+60,时间单位是h,温度单位为℃,t=0时表示中午12:00,则上午8:00时的温度为 ℃.
8
3.商店出售茶壶和茶杯,茶壶定价为每个20元,茶杯每个5元,该商店推出两种优惠办法:
①买一个茶壶赠一个茶杯;
②按总价的92%付款.
某顾客需购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯x(个),付款y(元),试分别建立两种优惠办法中y与x之间的函数解析式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更优惠
解:由优惠办法①可得函数解析式为y1=20×4+5(x-4)=5x+60(x≥4,且x∈N).
由优惠办法②可得y2=(5x+20×4)×92%=4.6x+73.6(x≥4,且x∈N).
y1-y2=0.4x-13.6(x≥4,且x∈N),
令y1-y2=0,得x=34.
所以,当购买34个茶杯时,两种优惠办法付款相同;
当4≤x<34时,y1
课堂小结
第1步:分析、联想、转化、抽象;
第2步:建立函数模型,把实际应用问题转化为数学问题;
第3步:解答数学问题,求得结果;
第4步:把数学结果转译成具体问题的结论,做出解答.
解答函数实际应用问题的步骤:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
