4.2.2 指数函数的图象和性质-高中数学人教A版必修一 课件(共26张PPT)
文档属性
| 名称 | 4.2.2 指数函数的图象和性质-高中数学人教A版必修一 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-25 16:58:50 | ||
图片预览






文档简介
(共26张PPT)
第四章 指数函数与对数函数
4.2 指数函数
4.2.2 指数函数的图象和性质
学习目标:
1.能画出具体指数函数的图象;
2.在观察指数函数图像基础上,归纳出指数函数的性质,能解决简单的问题;
3.在教学过程中通过类比,回顾归纳从图象和解析式这两种不同角度研究函数性质的数学方法,让学生在数学活动中体会数学思想方法之重要;
教学重点:指数函数的图象和性质.
教学难点:对底数的分类,如何由图象、解析式归纳指数函数的性质及其应用.
复习引入
函数y = ax(a 0,且a 1)叫做指数函数,其中x是自变量 .函数的定义域是R .
(1)定义域必须是实数集R;
(2)自变量是x,x位于指数位置上,且指数位置上只有x这一项;
(3)指数式只有一项,并且指数式的系数为1,例如y=5·ax(a>0且a≠1)不是指数函数;
(4)底数a的范围必须是a>0且a≠1.
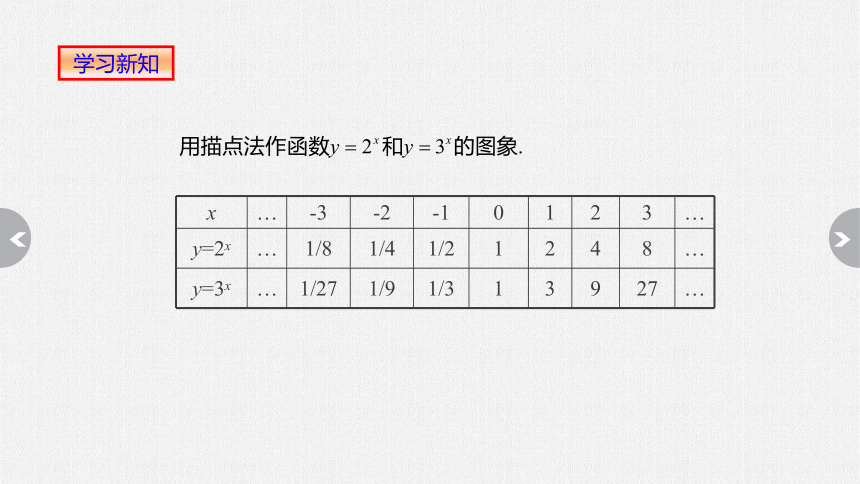
x … -3 -2 -1 0 1 2 3 …
y=2x … 1/8 1/4 1/2 1 2 4 8 …
y=3x … 1/27 1/9 1/3 1 3 9 27 …
学习新知
1
x
y
o
1
2
3
-1
-2
-3
学习新知
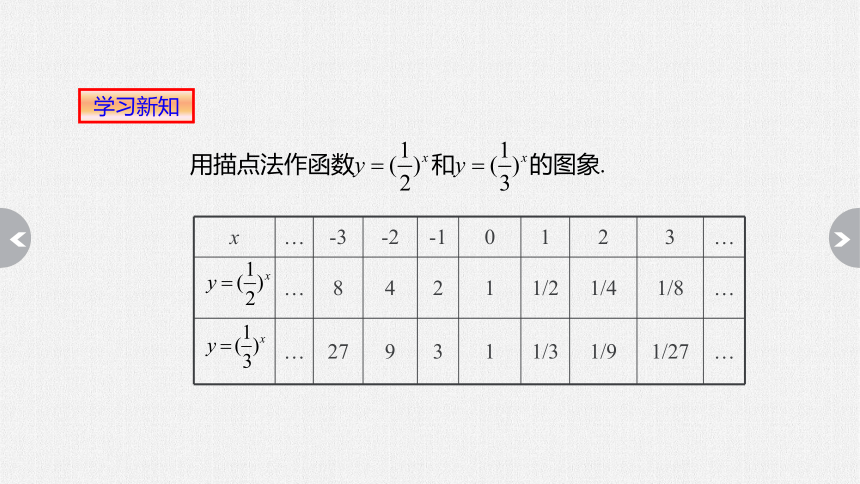
学习新知
x … -3 -2 -1 0 1 2 3 …
… 8 4 2 1 1/2 1/4 1/8 …
… 27 9 3 1 1/3 1/9 1/27 …
x
O
y
y=1
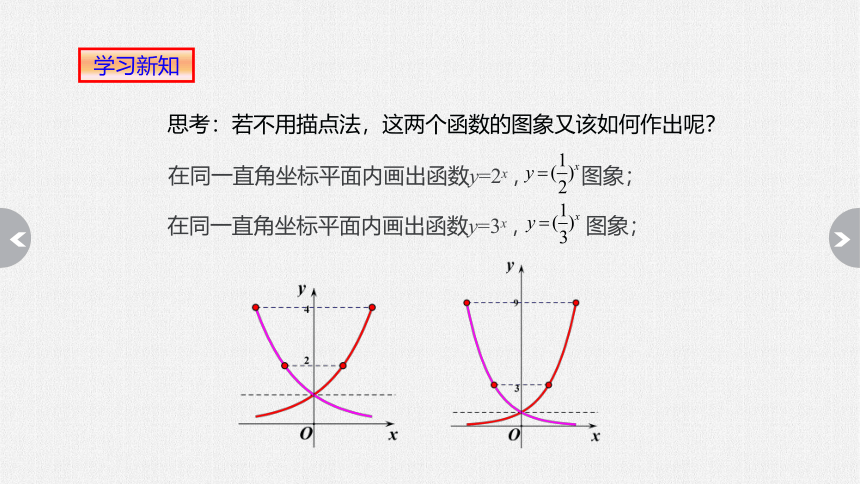
学习新知
思考:若不用描点法,这两个函数的图象又该如何作出呢?
在同一直角坐标平面内画出函数y=3x , 图象;
在同一直角坐标平面内画出函数y=2x , 图象;
学习新知
归纳:在同一直角坐标平面内,函数 图象关于y轴对称,即若点(x,y)在一个函数图象上,则(-x,y)在另一个函数图象上.
学习新知
观察右边图象,回答下列问题:
问题一:图象分别在哪几个象限?
问题二:图象的上升、下降与底数a有联系吗?
四个图象都在第____象限
Ⅰ、Ⅱ
x
O
y
y=1
y=3x
y = 2x
学习新知
观察右边图象,回答下列问题:
问题二:图象的上升、下降与底数a有联系吗?
x
O
y
y=1
y=3x
y = 2x
学习新知
当底数__ __时图象上升;
底数a由大变小时函数图像在第一象限内按____
时针方向旋转.
顺
当底数____时图象下降.
a>1
0观察右边图象,回答下列问题:
x
O
y
y=1
y=3x
y = 2x
学习新知
问题三:图象中有哪些特殊的点?
四个图象都经过点____.
图 象 a>1 0图 象 特 征
1.图象全在x轴上方,与x轴无限接近.
2.图象过定点(0,1)
3.分布在左下和右上两个区域内
3. 分布在左上和右下两个区域内
4.自左向右图象逐渐上升
4.自左向右图象逐渐下降
y=ax
(0y=1
y=ax
(a>1)
y=1
图 象 a>1 0性 质
y=ax
(0y=1
y=ax
(a>1)
y=1
1.定义域为(-∞,+ ∞ ),值域为(0,+ ∞ )
2.图像都过点(0,1),当x=0时,y=1
4.是R上的增函数
4.是R上的减函数
3.当x>0时,y>1;x<0时,03.当x>0时,01
例1.比较下列各题中两个值的大小:
解:
的底数是1.7,
由于底数1.7 >1,
利用函数单调性,
由2.5<3
所以
<
它们可以看成函数
当x分别取2.5和3时所对应的两个函数值.
典型例题
所以指数函数 在R上是增函数,
例1.比较下列各题中两个值的大小:
由于底数0.8 <1,
利用函数单调性,
由-0.1>-0.2
典型例题
解:
的底数是1.7,
它们可以看成函数
当x分别取-0.1和-0.2时所对应的两个函数值.
所以指数函数 在R上是减函数,
所以
例1.比较下列各题中两个值的大小:
典型例题
解: (3) ∵ f(x)=1.7x在(-∞,+∞)上是增函数,
又,0.3>0
∴ 1.70.3 =f(0.3)>f(0)=1
∴ 1.70.3 > 0.93.1
∵ g(x)=0.9x在(-∞,+∞)上是减函数,
又,3.1>0,
∴ 0.93.1 =g(3.1)f(x)=1.7x
g(x)=0.9x
y=1
比较大小:
巩固练习
<
>
(1)构造函数法:要点是利用函数的单调性,数的特征是同底不同指(包括可以化为同底的),若底数是参变量要注意分类讨论.比较两个同底数幂的大小时,可以构造一个指数函数,再利用指数函数的单调性即可比较大小.
(2)搭桥比较法:用别的数如0或1做桥.数的特征是不同底不同指.比较两个不同底数幂的大小时,通常引入第三个数作参照.
方法总结
例2. 如图,某城市人口呈指数增长.
(1) 根据图象,估计该城市人口每翻一番所需的时间(倍增期);
(2) 该城市人口从80万人开始,经过20年会增长到多少万人?
典型例题
解:(1)观察题目所给图,发现该城市人口经过20年约为10万人,经过40年约为20万人,即由10万人口增加到20万人口所用的时间约为20年,所以该城市人口每翻一番所需的时间为20年.
(2)因为倍增期为20年,所以每经过20年人口将翻一番.因此,从80万人开始,经过20年,该城市人口大约会增长到160万人.
典型例题
例3.解不等式
解:由指数函数的单调性可得:
整理得:
解得:
典型例题
原不等式的解集为:
由指数函数的单调性可得:
整理得:
解之得:
原不等式的解集为:
解下列不等式
①
②
巩固练习
解: 原不等式等价于:
①
解下列不等式
①
②
巩固练习
由指数函数的单调性可得:
解之得:
原不等式的解集为:
解: 原不等式等价于:
②
图 象 a>1 0性 质
y=ax
(0y=1
y=ax
(a>1)
y=1
1.定义域为(-∞,+ ∞ ),值域为(0,+ ∞ )
2.图像都过点(0,1),当x=0时,y=1
4.是R上的增函数
4.是R上的减函数
3.当x>0时,y>1;x<0时,03.当x>0时,01
课堂小结
课堂小结
指数比较大小的方法
①构造函数法:要点是利用函数的单调性,数的特征是同底不同指(包括可以化为同底的),若底数是参变量要注意分类讨论.
②搭桥比较法:用别的数如0或1做桥.数的特征是不同底不同指.
第四章 指数函数与对数函数
4.2 指数函数
4.2.2 指数函数的图象和性质
学习目标:
1.能画出具体指数函数的图象;
2.在观察指数函数图像基础上,归纳出指数函数的性质,能解决简单的问题;
3.在教学过程中通过类比,回顾归纳从图象和解析式这两种不同角度研究函数性质的数学方法,让学生在数学活动中体会数学思想方法之重要;
教学重点:指数函数的图象和性质.
教学难点:对底数的分类,如何由图象、解析式归纳指数函数的性质及其应用.
复习引入
函数y = ax(a 0,且a 1)叫做指数函数,其中x是自变量 .函数的定义域是R .
(1)定义域必须是实数集R;
(2)自变量是x,x位于指数位置上,且指数位置上只有x这一项;
(3)指数式只有一项,并且指数式的系数为1,例如y=5·ax(a>0且a≠1)不是指数函数;
(4)底数a的范围必须是a>0且a≠1.
x … -3 -2 -1 0 1 2 3 …
y=2x … 1/8 1/4 1/2 1 2 4 8 …
y=3x … 1/27 1/9 1/3 1 3 9 27 …
学习新知
1
x
y
o
1
2
3
-1
-2
-3
学习新知
学习新知
x … -3 -2 -1 0 1 2 3 …
… 8 4 2 1 1/2 1/4 1/8 …
… 27 9 3 1 1/3 1/9 1/27 …
x
O
y
y=1
学习新知
思考:若不用描点法,这两个函数的图象又该如何作出呢?
在同一直角坐标平面内画出函数y=3x , 图象;
在同一直角坐标平面内画出函数y=2x , 图象;
学习新知
归纳:在同一直角坐标平面内,函数 图象关于y轴对称,即若点(x,y)在一个函数图象上,则(-x,y)在另一个函数图象上.
学习新知
观察右边图象,回答下列问题:
问题一:图象分别在哪几个象限?
问题二:图象的上升、下降与底数a有联系吗?
四个图象都在第____象限
Ⅰ、Ⅱ
x
O
y
y=1
y=3x
y = 2x
学习新知
观察右边图象,回答下列问题:
问题二:图象的上升、下降与底数a有联系吗?
x
O
y
y=1
y=3x
y = 2x
学习新知
当底数__ __时图象上升;
底数a由大变小时函数图像在第一象限内按____
时针方向旋转.
顺
当底数____时图象下降.
a>1
0
x
O
y
y=1
y=3x
y = 2x
学习新知
问题三:图象中有哪些特殊的点?
四个图象都经过点____.
图 象 a>1 0
1.图象全在x轴上方,与x轴无限接近.
2.图象过定点(0,1)
3.分布在左下和右上两个区域内
3. 分布在左上和右下两个区域内
4.自左向右图象逐渐上升
4.自左向右图象逐渐下降
y=ax
(0
y=ax
(a>1)
y=1
图 象 a>1 0
y=ax
(0
y=ax
(a>1)
y=1
1.定义域为(-∞,+ ∞ ),值域为(0,+ ∞ )
2.图像都过点(0,1),当x=0时,y=1
4.是R上的增函数
4.是R上的减函数
3.当x>0时,y>1;x<0时,0
例1.比较下列各题中两个值的大小:
解:
的底数是1.7,
由于底数1.7 >1,
利用函数单调性,
由2.5<3
所以
<
它们可以看成函数
当x分别取2.5和3时所对应的两个函数值.
典型例题
所以指数函数 在R上是增函数,
例1.比较下列各题中两个值的大小:
由于底数0.8 <1,
利用函数单调性,
由-0.1>-0.2
典型例题
解:
的底数是1.7,
它们可以看成函数
当x分别取-0.1和-0.2时所对应的两个函数值.
所以指数函数 在R上是减函数,
所以
例1.比较下列各题中两个值的大小:
典型例题
解: (3) ∵ f(x)=1.7x在(-∞,+∞)上是增函数,
又,0.3>0
∴ 1.70.3 =f(0.3)>f(0)=1
∴ 1.70.3 > 0.93.1
∵ g(x)=0.9x在(-∞,+∞)上是减函数,
又,3.1>0,
∴ 0.93.1 =g(3.1)
g(x)=0.9x
y=1
比较大小:
巩固练习
<
>
(1)构造函数法:要点是利用函数的单调性,数的特征是同底不同指(包括可以化为同底的),若底数是参变量要注意分类讨论.比较两个同底数幂的大小时,可以构造一个指数函数,再利用指数函数的单调性即可比较大小.
(2)搭桥比较法:用别的数如0或1做桥.数的特征是不同底不同指.比较两个不同底数幂的大小时,通常引入第三个数作参照.
方法总结
例2. 如图,某城市人口呈指数增长.
(1) 根据图象,估计该城市人口每翻一番所需的时间(倍增期);
(2) 该城市人口从80万人开始,经过20年会增长到多少万人?
典型例题
解:(1)观察题目所给图,发现该城市人口经过20年约为10万人,经过40年约为20万人,即由10万人口增加到20万人口所用的时间约为20年,所以该城市人口每翻一番所需的时间为20年.
(2)因为倍增期为20年,所以每经过20年人口将翻一番.因此,从80万人开始,经过20年,该城市人口大约会增长到160万人.
典型例题
例3.解不等式
解:由指数函数的单调性可得:
整理得:
解得:
典型例题
原不等式的解集为:
由指数函数的单调性可得:
整理得:
解之得:
原不等式的解集为:
解下列不等式
①
②
巩固练习
解: 原不等式等价于:
①
解下列不等式
①
②
巩固练习
由指数函数的单调性可得:
解之得:
原不等式的解集为:
解: 原不等式等价于:
②
图 象 a>1 0
y=ax
(0
y=ax
(a>1)
y=1
1.定义域为(-∞,+ ∞ ),值域为(0,+ ∞ )
2.图像都过点(0,1),当x=0时,y=1
4.是R上的增函数
4.是R上的减函数
3.当x>0时,y>1;x<0时,0
课堂小结
课堂小结
指数比较大小的方法
①构造函数法:要点是利用函数的单调性,数的特征是同底不同指(包括可以化为同底的),若底数是参变量要注意分类讨论.
②搭桥比较法:用别的数如0或1做桥.数的特征是不同底不同指.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
