5.3 诱导公式(二)-高中数学人教A版必修一 课件(共22张PPT)
文档属性
| 名称 | 5.3 诱导公式(二)-高中数学人教A版必修一 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-25 17:07:52 | ||
图片预览








文档简介
(共22张PPT)
第五章 三角函数
5.3 诱导公式(二)
探究:
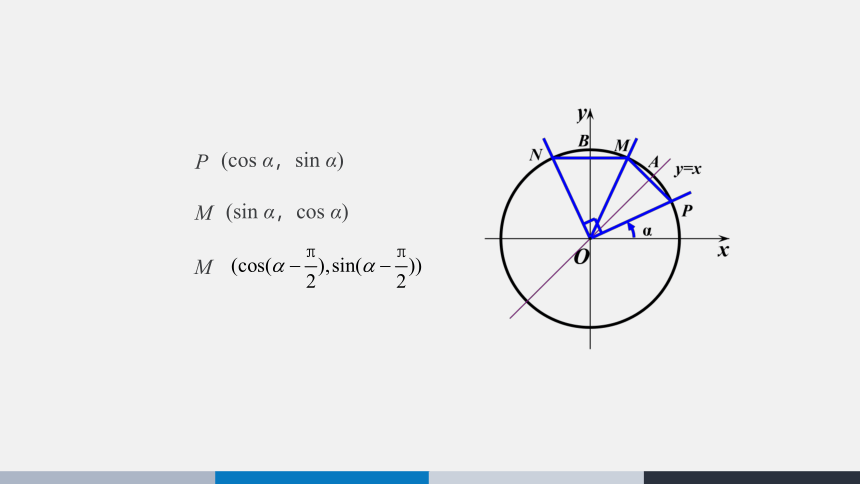
如图所示,设角 的终边与单位圆交于点P,则点P的坐标为______________.
点P关于直线y=x的对称点为M,点M 也在单位圆上,
则点M 的坐标为______________.
点M 关于直线y=x的对称点为N,点N 也在单位圆上,
则点N 的坐标为______________.
另一方面,点P经过以上两次轴对称变换到达点N,等同于点P沿单位圆旋转到点N,且旋转角的大小为∠PON=2(∠AOM+∠MOB)= .因
此点N是角
与单位圆的交点,点N坐标为 .
P
(cos α,sin α)
M
(sin α,cos α)
M
诱导公式(五)
sin α
cos α
P
(cos α,sin α)
N
(-sin α,cos α)
N
诱导公式(六)
-sin α
cos α
公式五和公式六可以概括如下:
的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成锐角时原函数值的符号.
公式一到公式四归纳:α+2kπ(k∈Z),-α,π±α的三角函数值,等于角α的同名三角函数值,前面加上一个把α看成锐角时原函数值的符号,简记为:“函数名不变,符号看象限”.
公式五和公式六归纳:
的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成锐角时原函数值的符号,简记为:“函数名改变,符号看象限”或“正变余、余变正、符号象限定”.
“奇变偶不变,符号看象限”
六组诱导公式可以统一概括为“ ”的诱导公式.当k为偶数时,函数名不改变;当k为奇数时,函数名改变;然后前面加一个把α视为锐角时原函数值的符号.记忆口诀为:
请你根据上述规律,完成下列等式:
你能根据相关的诱导公式给出上述等式的证明吗?
证明:
解:
例1. 已知 ,求 的值.
小结:利用诱导公式四和诱导公式五求值时,要注意沟通已知条件中的角和问题结论中角之间的联系,注意 与 ,
与 等互余角关系的识别和应用.
易错警示
利用诱导公式求三角函数值时,先将不是[0,2π)内的角的三角函数,转化为[0,2π)内的角的三角函数,或先将负角转化为正角后再用诱导公式转化到 范围内的角的三角函数值.
解:
例2. 已知 ,求 的值.
小结:解答本题时,应先利用诱导公式将已知式子和所求式分别化简,再利用sinθ±cosθ与sinθ·cosθ之间的关系求值.
例3. 已知
(1) 化简f(α);
(2) 若α是第三象限的角,且 ,求f(α)的值;
(3) 若 ,求f(α)的值.
(1)
又α是第三象限的角,
(2)
(3)
解:
这是一个与函数相结合的问题,解决此类问题时,可先用诱导公式化简变形,将三角函数的角度统一后再用同角三角函数关系式,这样可避免公式交错使用而导致的混乱.
课堂小结
1.诱导公式(五)
sin α
cos α
2.诱导公式(六)
-sin α
cos α
3.诱导公式统一成“ ”后,记忆口诀为“奇变偶不变,符号看象限”.
第五章 三角函数
5.3 诱导公式(二)
探究:
如图所示,设角 的终边与单位圆交于点P,则点P的坐标为______________.
点P关于直线y=x的对称点为M,点M 也在单位圆上,
则点M 的坐标为______________.
点M 关于直线y=x的对称点为N,点N 也在单位圆上,
则点N 的坐标为______________.
另一方面,点P经过以上两次轴对称变换到达点N,等同于点P沿单位圆旋转到点N,且旋转角的大小为∠PON=2(∠AOM+∠MOB)= .因
此点N是角
与单位圆的交点,点N坐标为 .
P
(cos α,sin α)
M
(sin α,cos α)
M
诱导公式(五)
sin α
cos α
P
(cos α,sin α)
N
(-sin α,cos α)
N
诱导公式(六)
-sin α
cos α
公式五和公式六可以概括如下:
的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成锐角时原函数值的符号.
公式一到公式四归纳:α+2kπ(k∈Z),-α,π±α的三角函数值,等于角α的同名三角函数值,前面加上一个把α看成锐角时原函数值的符号,简记为:“函数名不变,符号看象限”.
公式五和公式六归纳:
的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成锐角时原函数值的符号,简记为:“函数名改变,符号看象限”或“正变余、余变正、符号象限定”.
“奇变偶不变,符号看象限”
六组诱导公式可以统一概括为“ ”的诱导公式.当k为偶数时,函数名不改变;当k为奇数时,函数名改变;然后前面加一个把α视为锐角时原函数值的符号.记忆口诀为:
请你根据上述规律,完成下列等式:
你能根据相关的诱导公式给出上述等式的证明吗?
证明:
解:
例1. 已知 ,求 的值.
小结:利用诱导公式四和诱导公式五求值时,要注意沟通已知条件中的角和问题结论中角之间的联系,注意 与 ,
与 等互余角关系的识别和应用.
易错警示
利用诱导公式求三角函数值时,先将不是[0,2π)内的角的三角函数,转化为[0,2π)内的角的三角函数,或先将负角转化为正角后再用诱导公式转化到 范围内的角的三角函数值.
解:
例2. 已知 ,求 的值.
小结:解答本题时,应先利用诱导公式将已知式子和所求式分别化简,再利用sinθ±cosθ与sinθ·cosθ之间的关系求值.
例3. 已知
(1) 化简f(α);
(2) 若α是第三象限的角,且 ,求f(α)的值;
(3) 若 ,求f(α)的值.
(1)
又α是第三象限的角,
(2)
(3)
解:
这是一个与函数相结合的问题,解决此类问题时,可先用诱导公式化简变形,将三角函数的角度统一后再用同角三角函数关系式,这样可避免公式交错使用而导致的混乱.
课堂小结
1.诱导公式(五)
sin α
cos α
2.诱导公式(六)
-sin α
cos α
3.诱导公式统一成“ ”后,记忆口诀为“奇变偶不变,符号看象限”.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
