5.4.1 正弦函数、余弦函数的图象-高中数学人教A版必修一 课件(共25张PPT)
文档属性
| 名称 | 5.4.1 正弦函数、余弦函数的图象-高中数学人教A版必修一 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-25 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
第五章 三角函数
5.4 三角函数的图象与性质
5.4.1 正弦函数、余弦函数的图象
设实数x对应的角的正弦值为y,则对应关系y=sinx就是一个函数,称为正弦函数;同样y= cosx也是一个函数,称为余弦函数,这两个函数的定义域是什么?
一个函数总具有许多基本性质,要直观、全面了解正、余弦函数的基本特性,我们应从哪个方面入手?
前面我们在学习函数时,先作出函数的图象,再根据函数图象的的特点总结出函数的性质.我们怎样做出正弦函数和余弦函数的图象呢?
单位圆上任意一点在圆周上旋转一周就回到原来的位置,这一现象可以用公式
sin(x±2π) =sin x,cos(x±2π) =cos x
来表示.这说明,自变量每增加(减少)2π,正弦函数值、余弦函数值将重复出现.利用这一特性,就可以简化正弦函数、余弦函数的图象与性质的研究过程.
下面先研究函数y =sin x,x∈R的图象,从画函数y =sin x,x∈[0,2π]的图象开始.
思考:在[0,2π]上任取一个值x0,如何利用正弦函数的定义,确定正弦函数值sin x0,并画出点T(x0, sin x0)?
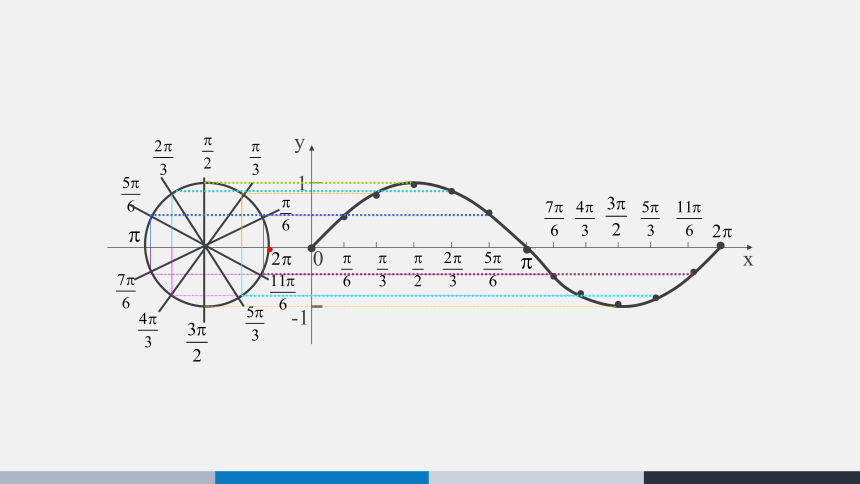
如图,在直角坐标系中画出以原点O为圆心的单位圆,⊙O与x轴正半轴的交点为A(1,0).在单位圆上,将点A绕着点O旋转x0弧度至点B,根据正弦函数的定义,点B的纵坐标y0 =sin x0.由此,以x0为横坐标, y0为纵坐标画点,即得到函数图象上的点T(x0, sin x0).
1
-1
0
y
x
●
●
●
●
●
●
●
●
●
●
●
●
●
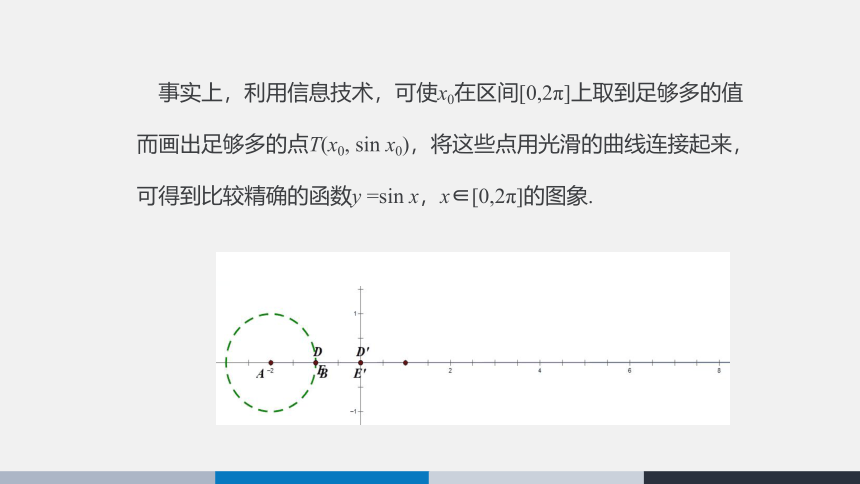
事实上,利用信息技术,可使x0在区间[0,2π]上取到足够多的值而画出足够多的点T(x0, sin x0),将这些点用光滑的曲线连接起来,可得到比较精确的函数y =sin x,x∈[0,2π]的图象.
终边相同角的三角函数值相等,即
sin(x±2kπ) =sin x,k∈Z
y =sin x,x∈[0,2π]
y =sin x,x∈R
f(x±2kπ) = f(x)
x
y
0
1
-1
y=sinx (x R)
利用图象平移
正弦函数的图象叫做正弦曲线,是一条“波浪起伏”的连续光滑曲线.
思考:在确定正弦函数的图象形状时,应抓住哪些关键点?
观察上图,在函数y =sin x,x∈[0,2π]的图象上,以下五个点:
在确定图象形状时起关键作用.描出这五个点,函数y =sin x,x∈[0,2π]的图象形状就基本确定了.因此,在精确度要求不高时,常先找到这五个关键点,再用光滑的曲线将它们连接起来,得到正弦函数的简图.这种近似的“五点(画图)法”是非常实用的.
正弦函数的“五点画图法”
0
x
y
1
-1
●
●
●
●
●
一般地,函数y=f(x+a)(a>0)的图象是由函数y=f(x)的图象经过怎样的变换而得到的?
向左平移a个单位.
想一想:设想由正弦函数的图象作出余弦函数的图象,那么先要将余弦函数y=cosx转化为正弦函数,你可以根据哪个公式完成这个转化?
对于函数y=cos x,由诱导公式 得,
而函数 的图象可以通过正弦函数
的图象向左平移 个单位长度而得到.
x∈R
x∈R
x∈R
所以,将函数的图象向左平移 个单位长度,就得到余弦函数的图象.
余弦函数y=cos x,x∈R的图象叫做余弦曲线,它是与正弦曲线具有相同形状的“波浪起伏”的连续光滑曲线.
函数y=cosx,x∈[0,2π]的图象如何?其中起关键作用的点有哪几个?
x
y
O
2π
π
1
-1
例1. 画出下列函数的简图.
(1) y=1+sin x,x∈[0,2π];
解:
(1) 按五个关键点列表:
x 0 π 2π
sin x 0 1 0 -1 0
1+sin x 1 2 1 0 1
描点并将它们用光滑的曲线连接起来:
解:
(2) 按五个关键点列表:
x 0 π 2π
cos x 1 0 -1 0 1
-cos x -1 0 1 0 -1
例1. 画出下列函数的简图.
(2) y=-cos x,x∈[0,2π].
描点并将它们用光滑的曲线连接起来:
练习:(1)画出函数y=-sinx x∈ [0,2π]
(2)画出函数y=1+cosx x∈ [0,2π]
(3)画出函数y=2sinx x∈ [0,2π]
1.正、余弦函数的图象每相隔2π个单位重复出现,因此,只要记住它们在[0,2π]内的图象形态,就可以画出正弦曲线和余弦曲线.
2.作与正、余弦函数有关的函数图象,是解题的基本要求,用“五点法”作图是常用的方法.
课堂小结
3.正、余弦函数的图象不仅是进一步研究函数性质的基础,也是解决有关三角函数问题的工具,这是一种数形结合的数学思想.
第五章 三角函数
5.4 三角函数的图象与性质
5.4.1 正弦函数、余弦函数的图象
设实数x对应的角的正弦值为y,则对应关系y=sinx就是一个函数,称为正弦函数;同样y= cosx也是一个函数,称为余弦函数,这两个函数的定义域是什么?
一个函数总具有许多基本性质,要直观、全面了解正、余弦函数的基本特性,我们应从哪个方面入手?
前面我们在学习函数时,先作出函数的图象,再根据函数图象的的特点总结出函数的性质.我们怎样做出正弦函数和余弦函数的图象呢?
单位圆上任意一点在圆周上旋转一周就回到原来的位置,这一现象可以用公式
sin(x±2π) =sin x,cos(x±2π) =cos x
来表示.这说明,自变量每增加(减少)2π,正弦函数值、余弦函数值将重复出现.利用这一特性,就可以简化正弦函数、余弦函数的图象与性质的研究过程.
下面先研究函数y =sin x,x∈R的图象,从画函数y =sin x,x∈[0,2π]的图象开始.
思考:在[0,2π]上任取一个值x0,如何利用正弦函数的定义,确定正弦函数值sin x0,并画出点T(x0, sin x0)?
如图,在直角坐标系中画出以原点O为圆心的单位圆,⊙O与x轴正半轴的交点为A(1,0).在单位圆上,将点A绕着点O旋转x0弧度至点B,根据正弦函数的定义,点B的纵坐标y0 =sin x0.由此,以x0为横坐标, y0为纵坐标画点,即得到函数图象上的点T(x0, sin x0).
1
-1
0
y
x
●
●
●
●
●
●
●
●
●
●
●
●
●
事实上,利用信息技术,可使x0在区间[0,2π]上取到足够多的值而画出足够多的点T(x0, sin x0),将这些点用光滑的曲线连接起来,可得到比较精确的函数y =sin x,x∈[0,2π]的图象.
终边相同角的三角函数值相等,即
sin(x±2kπ) =sin x,k∈Z
y =sin x,x∈[0,2π]
y =sin x,x∈R
f(x±2kπ) = f(x)
x
y
0
1
-1
y=sinx (x R)
利用图象平移
正弦函数的图象叫做正弦曲线,是一条“波浪起伏”的连续光滑曲线.
思考:在确定正弦函数的图象形状时,应抓住哪些关键点?
观察上图,在函数y =sin x,x∈[0,2π]的图象上,以下五个点:
在确定图象形状时起关键作用.描出这五个点,函数y =sin x,x∈[0,2π]的图象形状就基本确定了.因此,在精确度要求不高时,常先找到这五个关键点,再用光滑的曲线将它们连接起来,得到正弦函数的简图.这种近似的“五点(画图)法”是非常实用的.
正弦函数的“五点画图法”
0
x
y
1
-1
●
●
●
●
●
一般地,函数y=f(x+a)(a>0)的图象是由函数y=f(x)的图象经过怎样的变换而得到的?
向左平移a个单位.
想一想:设想由正弦函数的图象作出余弦函数的图象,那么先要将余弦函数y=cosx转化为正弦函数,你可以根据哪个公式完成这个转化?
对于函数y=cos x,由诱导公式 得,
而函数 的图象可以通过正弦函数
的图象向左平移 个单位长度而得到.
x∈R
x∈R
x∈R
所以,将函数的图象向左平移 个单位长度,就得到余弦函数的图象.
余弦函数y=cos x,x∈R的图象叫做余弦曲线,它是与正弦曲线具有相同形状的“波浪起伏”的连续光滑曲线.
函数y=cosx,x∈[0,2π]的图象如何?其中起关键作用的点有哪几个?
x
y
O
2π
π
1
-1
例1. 画出下列函数的简图.
(1) y=1+sin x,x∈[0,2π];
解:
(1) 按五个关键点列表:
x 0 π 2π
sin x 0 1 0 -1 0
1+sin x 1 2 1 0 1
描点并将它们用光滑的曲线连接起来:
解:
(2) 按五个关键点列表:
x 0 π 2π
cos x 1 0 -1 0 1
-cos x -1 0 1 0 -1
例1. 画出下列函数的简图.
(2) y=-cos x,x∈[0,2π].
描点并将它们用光滑的曲线连接起来:
练习:(1)画出函数y=-sinx x∈ [0,2π]
(2)画出函数y=1+cosx x∈ [0,2π]
(3)画出函数y=2sinx x∈ [0,2π]
1.正、余弦函数的图象每相隔2π个单位重复出现,因此,只要记住它们在[0,2π]内的图象形态,就可以画出正弦曲线和余弦曲线.
2.作与正、余弦函数有关的函数图象,是解题的基本要求,用“五点法”作图是常用的方法.
课堂小结
3.正、余弦函数的图象不仅是进一步研究函数性质的基础,也是解决有关三角函数问题的工具,这是一种数形结合的数学思想.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
