5.4.2 正弦函数、余弦函数的性质(一)-高中数学人教A版必修一 课件(共18张PPT)
文档属性
| 名称 | 5.4.2 正弦函数、余弦函数的性质(一)-高中数学人教A版必修一 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-25 17:09:53 | ||
图片预览




文档简介
(共18张PPT)
第五章 三角函数
5.4 三角函数的图象与性质
5.4.2 正弦函数、余弦函数的性质(一)
今天是星期二,则过了3天是星期几?过了7天呢?
过了100天呢?……
每年都有春夏秋冬,它们周而复始的变化着.
月亮圆缺—潮汐变化
咏月
——唐·李建枢
昨夜圆非今日圆,
却疑圆处减婵娟.
一年十二度圆缺,
能得几多时少年?
如果一个函数也存在周期现象,那它就是一个周期函数.
比如:函数f(x)(x∈N*)满足以下规律:
周期函数
那么函数 就叫做周期函数.
非零常数T 叫做这个函数的周期.
对于函数 而言,如果存在一个非零常数T ,使得当x 取定义域内的每一个值时,都有
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
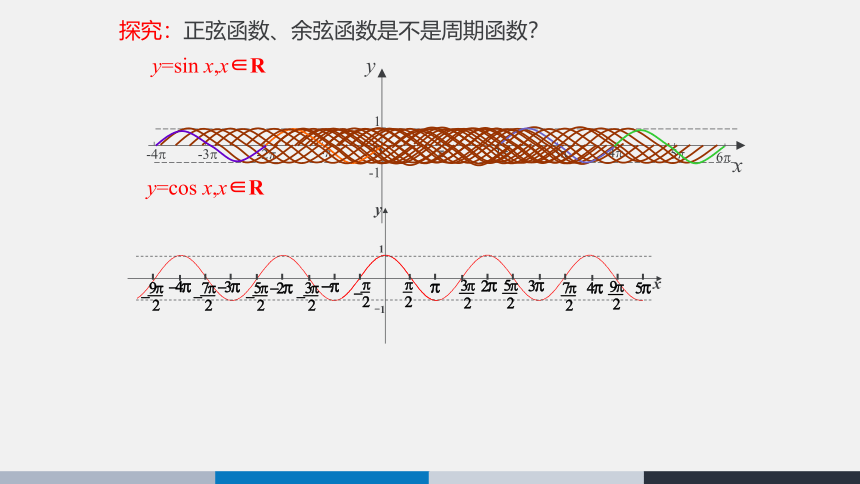
探究:正弦函数、余弦函数是不是周期函数?
x
y
1
-1
y=sin x,x∈R
y=cos x,x∈R
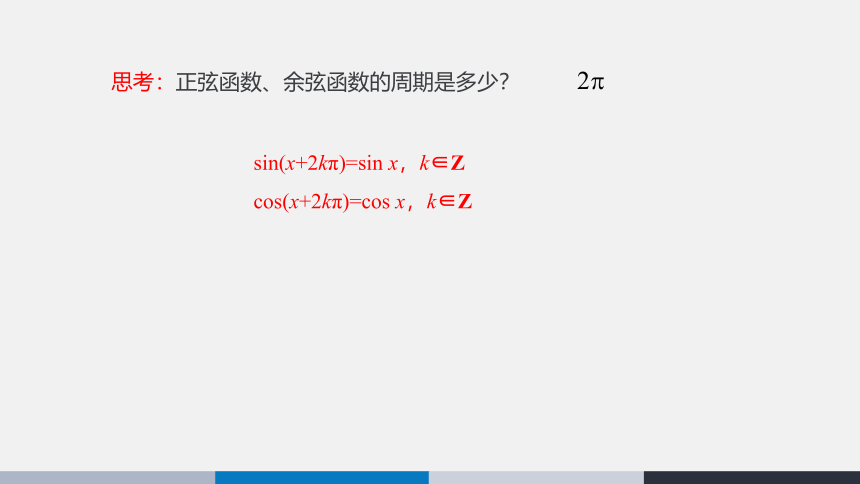
思考:正弦函数、余弦函数的周期是多少?
sin(x+2kπ)=sin x,k∈Z
cos(x+2kπ)=cos x,k∈Z
如果在周期函数 f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做 f(x)的最小正周期.
声明:今后所涉及的周期,在没有特别说明的前提下,都是指函数的最小正周期.
例1:利用周期函数的定义求下列函数的最小正周期.
(1)y=3cos x,x∈R T=2π
(2)y=sin 2x,x∈R T=π
(3)y=2sin(x+ ),x∈R T=4π
(4)y=3cos(x+),x∈R T=8π
思考:回顾例1的解答过程,你能发现这些函数的周期与解析式中哪些量有关吗?
(1)y=sin x,x∈R; π
(2)y=cos 4x,x∈R ;
(3)y=cos(x- ),x∈R; π
(4)y=sin (x+),x∈R; 6π
y
x
o
-
-1
2
3
4
-2
-3
1
正弦、余弦函数的性质——奇偶性
y=sinx
正弦函数是奇函数
x
y
1
-1
余弦函数是偶函数
y=cosx
正弦函数是奇函数,余弦函数是偶函数.
巩固练习:
奇函数
奇函数
奇函数
偶函数
O
y
x
O
y
x
A
O
y
x
B
O
y
x
C
D
2.特殊点:函数与x轴、y轴的交点,f(x)的正负
课堂小结
正弦函数是奇函数,余弦函数是偶函数.
数形结合思想
T=2π
第五章 三角函数
5.4 三角函数的图象与性质
5.4.2 正弦函数、余弦函数的性质(一)
今天是星期二,则过了3天是星期几?过了7天呢?
过了100天呢?……
每年都有春夏秋冬,它们周而复始的变化着.
月亮圆缺—潮汐变化
咏月
——唐·李建枢
昨夜圆非今日圆,
却疑圆处减婵娟.
一年十二度圆缺,
能得几多时少年?
如果一个函数也存在周期现象,那它就是一个周期函数.
比如:函数f(x)(x∈N*)满足以下规律:
周期函数
那么函数 就叫做周期函数.
非零常数T 叫做这个函数的周期.
对于函数 而言,如果存在一个非零常数T ,使得当x 取定义域内的每一个值时,都有
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
探究:正弦函数、余弦函数是不是周期函数?
x
y
1
-1
y=sin x,x∈R
y=cos x,x∈R
思考:正弦函数、余弦函数的周期是多少?
sin(x+2kπ)=sin x,k∈Z
cos(x+2kπ)=cos x,k∈Z
如果在周期函数 f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做 f(x)的最小正周期.
声明:今后所涉及的周期,在没有特别说明的前提下,都是指函数的最小正周期.
例1:利用周期函数的定义求下列函数的最小正周期.
(1)y=3cos x,x∈R T=2π
(2)y=sin 2x,x∈R T=π
(3)y=2sin(x+ ),x∈R T=4π
(4)y=3cos(x+),x∈R T=8π
思考:回顾例1的解答过程,你能发现这些函数的周期与解析式中哪些量有关吗?
(1)y=sin x,x∈R; π
(2)y=cos 4x,x∈R ;
(3)y=cos(x- ),x∈R; π
(4)y=sin (x+),x∈R; 6π
y
x
o
-
-1
2
3
4
-2
-3
1
正弦、余弦函数的性质——奇偶性
y=sinx
正弦函数是奇函数
x
y
1
-1
余弦函数是偶函数
y=cosx
正弦函数是奇函数,余弦函数是偶函数.
巩固练习:
奇函数
奇函数
奇函数
偶函数
O
y
x
O
y
x
A
O
y
x
B
O
y
x
C
D
2.特殊点:函数与x轴、y轴的交点,f(x)的正负
课堂小结
正弦函数是奇函数,余弦函数是偶函数.
数形结合思想
T=2π
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
