2023年辽宁省营口市中考数学模拟练习卷(七)(含答案)
文档属性
| 名称 | 2023年辽宁省营口市中考数学模拟练习卷(七)(含答案) | 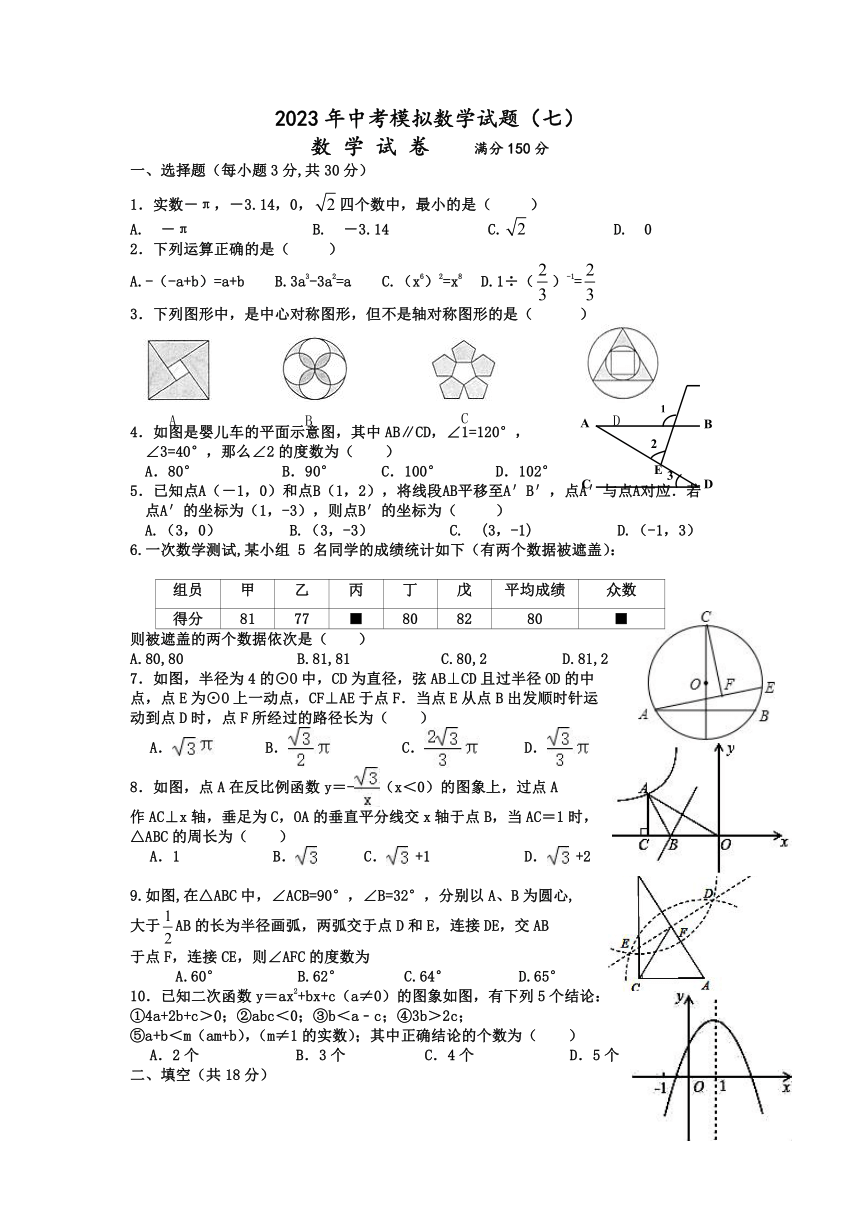 | |
| 格式 | doc | ||
| 文件大小 | 302.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-25 22:28:45 | ||
图片预览


文档简介
2023年中考模拟数学试题(七)
数 学 试 卷 满分150分
一、选择题(每小题3分,共30分)
1.实数-π,-3.14,0,四个数中,最小的是( )
A. -π B. -3.14 C. D. 0
2.下列运算正确的是( )
A.-(-a+b)=a+b B.3a3-3a2=a C.(x6)2=x8 D.1÷()-1=
3.下列图形中,是中心对称图形,但不是轴对称图形的是( )
4.如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,
∠3=40°,那么∠2的度数为( )
A.80° B.90° C.100° D.102°
5.已知点A(-1,0)和点B(1,2),将线段AB平移至A′B′,点A′与点A对应.若
点A′的坐标为(1,-3),则点B′的坐标为( )
A.(3,0) B.(3,-3) C. (3,-1) D.(-1,3)
6.一次数学测试,某小组 5 名同学的成绩统计如下(有两个数据被遮盖):
组员 甲 乙 丙 丁 戊 平均成绩 众数
得分 81 77 ■ 80 82 80 ■
则被遮盖的两个数据依次是( )
A.80,80 B.81,81 C.80,2 D.81,2
7.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中
点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运
动到点D时,点F所经过的路径长为( )
A. B. C. D.
8.如图,点A在反比例函数y=-(x<0)的图象上,过点A
作AC⊥x轴,垂足为C,OA的垂直平分线交x轴于点B,当AC=1时,
△ABC的周长为( )
A.1 B. C. +1 D. +2
9.如图,在△ABC中,∠ACB=90°,∠B=32°,分别以A、B为圆心,
大于AB的长为半径画弧,两弧交于点D和E,连接DE,交AB
于点F,连接CE,则∠AFC的度数为
A.60° B.62° C.64° D.65°
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:
①4a+2b+c>0;②abc<0;③b<a﹣c;④3b>2c;
⑤a+b<m(am+b),(m≠1的实数);其中正确结论的个数为( )
A.2个 B.3个 C.4个 D.5个
二、填空(共18分)
11.要使代数式有意义,x的取值范围是 .
12.分解因式 a3-4a2b+4ab2= ▲ .
13.南海是我国固有领海,南海面积超过东海、黄海、渤海面积的总和,约为360万平方
千米. 360万平方千米用科学计数法可表示为 ▲ 平方千米.
14.在一个不透明的口袋中装有若干个只有颜色不同的球,如果口袋中
装有3个红球,且摸出红球的概率为,那么袋中共有 ▲ 个球.
15. 如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切
于点D,交AB于点E, 交AC于点F,点P是⊙A上的一点,且∠EPF=450,
图中阴影影部分的面积为
16. 如图,已知A1、A2、A3、…、An、An+1是x轴上的点,
OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1
作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,
连接A1B2、B1A2、B2A3、…、AnBn+1、BnAn+1,依次相交于
点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面
积依次记为S1、S2、S3、…、Sn,则Sn为 .
三、解答题(102分)
17.(10分)先化简,再求值:(1﹣)÷,其中a=+2
18. (10分)在复习《反比例函数》一课时,同桌的小峰和小轩有一个问题观点不一致:
情境:随机同时掷两枚质地均匀的骰子(骰子六个面上的点数分别代表1,2,3,4,5,6). 第一枚骰子上的点数作为点P(m,n)的横坐标,第二枚骰子上的点数作为点P(m,n)的纵坐标.小峰认为:点P(m,n)在反比例函数y=图象上的概率一定大于在反比例函数y=图象上的概率;小轩认为:点P(m,n)在反比例函数y=和y=图象上的概率相同.问题:
(1)试用列表或画树状图的方法,列举出所有点P(m,n)的情形;
(2)分别求出点P(m,n)在两个反比例函数的图象上的概率,并说明谁的观点正确.
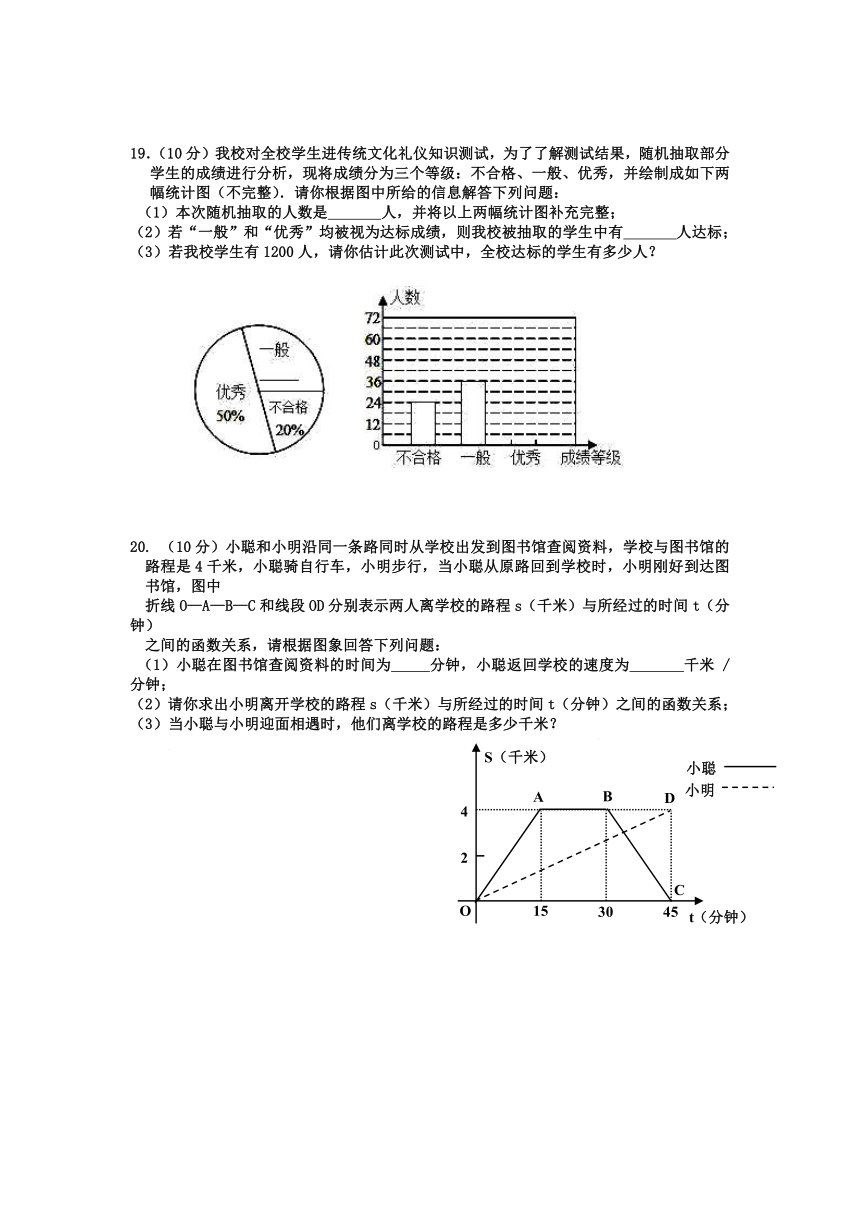
19.(10分)我校对全校学生进传统文化礼仪知识测试,为了了解测试结果,随机抽取部分学生的成绩进行分析,现将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:
(1)本次随机抽取的人数是 人,并将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则我校被抽取的学生中有 人达标;
(3)若我校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
20. (10分)小聪和小明沿同一条路同时从学校出发到图书馆查阅资料,学校与图书馆的路程是4千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中
折线O—A—B—C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)
之间的函数关系,请根据图象回答下列问题:
(1)小聪在图书馆查阅资料的时间为 分钟,小聪返回学校的速度为 千米 /分钟;
(2)请你求出小明离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
21.(10分)如图,在一笔直的海岸线上有A、B两上观测站,A在B的正东方向,BP=6(单位:km).有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得
小船在北偏东45°的方向.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向进行沿途考察,求观测站B到射线AP的最短距离.
22. (12分)如图,在△ABC中,∠ABC=90,AB=6,BC=8。以AB为直径的⊙O
交AC于D,E是BC的中点,连接ED并延长交BA的延长线于点F。
(1)求证:DE是⊙O的切线;
(2)求DB的长;
(3)求S△FAD∶S△FDB的值
23.(12分)某工厂制作A,B两种手工艺品,B每件获利比A多105元,获利30元的A与获利240元的B数量相等.
(1)制作一件A和一件B分别获利多少元?
(2)工厂安排65人制作A,B两种手工艺品,每人每天制作2件A或1件B.现在在不增加工人的情况下,增加制作C.已知每人每天可制作1件C(每人每天只能制作一种手工艺品),要求每天制作A,C两种手工艺品的数量相等.设每天安排x人制作B,y人制作A,写出y与x之间的函数关系式.
(3)在(1)(2)的条件下,每天制作B不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知C每件获利30元,求每天制作三种手工艺品可获得的总利润W(元)的最大值及相应x的值.
24. (14分) 在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),
∠BPE=∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1) 当点P与点C重合时(如图①).求证:△BOG≌△POE;
(2)通过观察、测量、猜想:= ▲ ,并结合图②证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图③),若∠ACB=,求的值.
(用含的式子表示)
25.(14分)如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.点D是直线BC上方抛物线上一动点.
(1)求抛物线的解析式;
(2)如图1,连接BD、CD,设点D的横坐标为m,△BCD的面积为s.试求出s与m的函数关系式,
并求出s的最大值;
(3)如图2,设AB的中点为E,作DF⊥BC,垂足为F,连接CD、CE,是否存在点D,使得以C、D,F三点为顶点的三角形与△CEO相似?若存在,请直接写出点D的坐标;若不存在,请说明理由.
数学参考答案(七)
一、ADAAC ADCCB
二、11.x>0且x≠1 12.a(a-2b)2 13.3.6×106 14.9 15.4- 16.
三、17.1+
18.(1)略 (2)都不正确
19.(1)120人 (2)96 (3)960
20.(1)15, (2)y=x (0≤x≤45)(3)3千米
21.(1)6+6 (2) 3+3
22.(1)略 (2) (3)
23.(1)A15元,B120元 (2)y=-x+ (3)A13人,B26人,C26人时利润最大,为3198元。
24.(1)略 (2) (3)tanα
25.(1)y=-x2+2x+3(2)m=时,S值最大为(3)D(,)或(,)
A
B
C
D
2
A
B
C
D
E
1
3
C
O
A
B
D
2
4
15
30
45
S(千米)
t(分钟)
小聪
小明
A
B
C(P)
D
E
F
O
G
图①
A
B
C
D
P
E
O
G
F
图②
A
B
C
D
P
E
F
O
G
图③
数 学 试 卷 满分150分
一、选择题(每小题3分,共30分)
1.实数-π,-3.14,0,四个数中,最小的是( )
A. -π B. -3.14 C. D. 0
2.下列运算正确的是( )
A.-(-a+b)=a+b B.3a3-3a2=a C.(x6)2=x8 D.1÷()-1=
3.下列图形中,是中心对称图形,但不是轴对称图形的是( )
4.如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,
∠3=40°,那么∠2的度数为( )
A.80° B.90° C.100° D.102°
5.已知点A(-1,0)和点B(1,2),将线段AB平移至A′B′,点A′与点A对应.若
点A′的坐标为(1,-3),则点B′的坐标为( )
A.(3,0) B.(3,-3) C. (3,-1) D.(-1,3)
6.一次数学测试,某小组 5 名同学的成绩统计如下(有两个数据被遮盖):
组员 甲 乙 丙 丁 戊 平均成绩 众数
得分 81 77 ■ 80 82 80 ■
则被遮盖的两个数据依次是( )
A.80,80 B.81,81 C.80,2 D.81,2
7.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中
点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运
动到点D时,点F所经过的路径长为( )
A. B. C. D.
8.如图,点A在反比例函数y=-(x<0)的图象上,过点A
作AC⊥x轴,垂足为C,OA的垂直平分线交x轴于点B,当AC=1时,
△ABC的周长为( )
A.1 B. C. +1 D. +2
9.如图,在△ABC中,∠ACB=90°,∠B=32°,分别以A、B为圆心,
大于AB的长为半径画弧,两弧交于点D和E,连接DE,交AB
于点F,连接CE,则∠AFC的度数为
A.60° B.62° C.64° D.65°
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:
①4a+2b+c>0;②abc<0;③b<a﹣c;④3b>2c;
⑤a+b<m(am+b),(m≠1的实数);其中正确结论的个数为( )
A.2个 B.3个 C.4个 D.5个
二、填空(共18分)
11.要使代数式有意义,x的取值范围是 .
12.分解因式 a3-4a2b+4ab2= ▲ .
13.南海是我国固有领海,南海面积超过东海、黄海、渤海面积的总和,约为360万平方
千米. 360万平方千米用科学计数法可表示为 ▲ 平方千米.
14.在一个不透明的口袋中装有若干个只有颜色不同的球,如果口袋中
装有3个红球,且摸出红球的概率为,那么袋中共有 ▲ 个球.
15. 如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切
于点D,交AB于点E, 交AC于点F,点P是⊙A上的一点,且∠EPF=450,
图中阴影影部分的面积为
16. 如图,已知A1、A2、A3、…、An、An+1是x轴上的点,
OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1
作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,
连接A1B2、B1A2、B2A3、…、AnBn+1、BnAn+1,依次相交于
点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面
积依次记为S1、S2、S3、…、Sn,则Sn为 .
三、解答题(102分)
17.(10分)先化简,再求值:(1﹣)÷,其中a=+2
18. (10分)在复习《反比例函数》一课时,同桌的小峰和小轩有一个问题观点不一致:
情境:随机同时掷两枚质地均匀的骰子(骰子六个面上的点数分别代表1,2,3,4,5,6). 第一枚骰子上的点数作为点P(m,n)的横坐标,第二枚骰子上的点数作为点P(m,n)的纵坐标.小峰认为:点P(m,n)在反比例函数y=图象上的概率一定大于在反比例函数y=图象上的概率;小轩认为:点P(m,n)在反比例函数y=和y=图象上的概率相同.问题:
(1)试用列表或画树状图的方法,列举出所有点P(m,n)的情形;
(2)分别求出点P(m,n)在两个反比例函数的图象上的概率,并说明谁的观点正确.
19.(10分)我校对全校学生进传统文化礼仪知识测试,为了了解测试结果,随机抽取部分学生的成绩进行分析,现将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:
(1)本次随机抽取的人数是 人,并将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则我校被抽取的学生中有 人达标;
(3)若我校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
20. (10分)小聪和小明沿同一条路同时从学校出发到图书馆查阅资料,学校与图书馆的路程是4千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中
折线O—A—B—C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)
之间的函数关系,请根据图象回答下列问题:
(1)小聪在图书馆查阅资料的时间为 分钟,小聪返回学校的速度为 千米 /分钟;
(2)请你求出小明离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
21.(10分)如图,在一笔直的海岸线上有A、B两上观测站,A在B的正东方向,BP=6(单位:km).有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得
小船在北偏东45°的方向.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向进行沿途考察,求观测站B到射线AP的最短距离.
22. (12分)如图,在△ABC中,∠ABC=90,AB=6,BC=8。以AB为直径的⊙O
交AC于D,E是BC的中点,连接ED并延长交BA的延长线于点F。
(1)求证:DE是⊙O的切线;
(2)求DB的长;
(3)求S△FAD∶S△FDB的值
23.(12分)某工厂制作A,B两种手工艺品,B每件获利比A多105元,获利30元的A与获利240元的B数量相等.
(1)制作一件A和一件B分别获利多少元?
(2)工厂安排65人制作A,B两种手工艺品,每人每天制作2件A或1件B.现在在不增加工人的情况下,增加制作C.已知每人每天可制作1件C(每人每天只能制作一种手工艺品),要求每天制作A,C两种手工艺品的数量相等.设每天安排x人制作B,y人制作A,写出y与x之间的函数关系式.
(3)在(1)(2)的条件下,每天制作B不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知C每件获利30元,求每天制作三种手工艺品可获得的总利润W(元)的最大值及相应x的值.
24. (14分) 在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),
∠BPE=∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1) 当点P与点C重合时(如图①).求证:△BOG≌△POE;
(2)通过观察、测量、猜想:= ▲ ,并结合图②证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图③),若∠ACB=,求的值.
(用含的式子表示)
25.(14分)如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.点D是直线BC上方抛物线上一动点.
(1)求抛物线的解析式;
(2)如图1,连接BD、CD,设点D的横坐标为m,△BCD的面积为s.试求出s与m的函数关系式,
并求出s的最大值;
(3)如图2,设AB的中点为E,作DF⊥BC,垂足为F,连接CD、CE,是否存在点D,使得以C、D,F三点为顶点的三角形与△CEO相似?若存在,请直接写出点D的坐标;若不存在,请说明理由.
数学参考答案(七)
一、ADAAC ADCCB
二、11.x>0且x≠1 12.a(a-2b)2 13.3.6×106 14.9 15.4- 16.
三、17.1+
18.(1)略 (2)都不正确
19.(1)120人 (2)96 (3)960
20.(1)15, (2)y=x (0≤x≤45)(3)3千米
21.(1)6+6 (2) 3+3
22.(1)略 (2) (3)
23.(1)A15元,B120元 (2)y=-x+ (3)A13人,B26人,C26人时利润最大,为3198元。
24.(1)略 (2) (3)tanα
25.(1)y=-x2+2x+3(2)m=时,S值最大为(3)D(,)或(,)
A
B
C
D
2
A
B
C
D
E
1
3
C
O
A
B
D
2
4
15
30
45
S(千米)
t(分钟)
小聪
小明
A
B
C(P)
D
E
F
O
G
图①
A
B
C
D
P
E
O
G
F
图②
A
B
C
D
P
E
F
O
G
图③
同课章节目录
