2023年辽宁省营口市中考数学模拟练习卷(三)(含答案)
文档属性
| 名称 | 2023年辽宁省营口市中考数学模拟练习卷(三)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 359.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-26 07:36:48 | ||
图片预览



文档简介
2023年中考模拟数学试题(三)
数 学 试 卷 满分150分
一、选择题(每小题3分,共30分)
1.﹣的相反数是( ) A.2 B. C.﹣2 D.﹣
2.每年的5月17日全国助残日,今年全国助残日的主题是“关注孤独症儿童,走向美好未来”.第二次全国残疾人抽样调查结果显示,我国0~6岁精神残疾儿童约为11.1万人.11.1万用科学记数法表示为( )
A.1.11×104 B.11.1×104 C.1.11×105 D.1.11×106
3.图所示的几何体的俯视图是( )
A. B. C. D.
4.下列运算正确的是( )
A.+= B.x8÷x2=x6 C.×= D.(a5)2=a7
第6题图 第8题图 第9题图
5.下列说法正确的是( )
A.一组数据2,2,3,4,这组数据的中位数是2
B.了解一批灯泡的使用寿命的情况,适合抽样调查
C.小明的三次数学成绩是126分,130分,136分,则小明这三次成绩的平均数是131分
D.某日最高气温是7℃,最低气温是﹣2℃,则该日气温的极差是5℃
6.如图,点E是 ABCD的边AD上的一点,且,连接BE并延长交CD的延长线于点F,若DE=3,DF=4,则 ABCD的周长为( )
A.21 B.28 C.34 D.42
7.随着5G网络技术的发展,市场对5G产品的需求越来越大,为满足市场需求,某大型5G产品生产厂家更新技术后,加快了生产速度,现在平均每天比更新技术前多生产30万件产品,现在生产500万件产品所需时间与更新技术前生产400万件产品所需时间相同.设更新技术前每天生产x万件产品,依题意得( )
A.= B.= C.= D.=
8.如图,已知⊙O的半径为2,△ABC内接于⊙O,∠ACB=135°,则AB=( )
A.4 B. C. D.
9.如图,在锐角三角形ABC中,BC=4,∠ABC=60°,BD平分∠ABC,交AC于点D,M,N分别是BD,BC上的动点,则CM+MN的最小值是( )
A. B.2 C.2 D.4
10.已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c<0;②a﹣b+c>1;③abc>0;④9a﹣3b+c<0;⑤c﹣a>1.其中所有正确结论的序号是( )
A.①② B.①③④ C.①②③④ D.①②③④⑤
第10题图 第14题图 第15题图 第16题图
二、填空题(每小题3分,共18分)
11.代数式在实数范围内有意义,则实数x的取值范围是 .
12.分解因式:a3﹣2a2+a= .
13.圆锥的底面半径为3,侧面积为12π,则这个圆锥的母线长为 .
14.在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是 ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的大小是 .
15.如图,点A是x轴负半轴上任意一点,过点A作y轴的平行线,分别与反比例函数y=﹣和y=的图象交于点B和C点,若D为y轴上任意一点,连接DC、DB,则△BCD的面积为 .
16.如图,在平面直角坐标系中,直线l1:y=x+与x轴交于点A1,与y轴交于点A2,过点A1作x轴的垂线交直线l2:y=x于点B1,过点A1作A1B1的垂线交y轴于点B2,此时点B2与原点O重合,连接A2B1交x轴于点C1,得到第1个△C1B1B2;过点A2作y轴的垂线交l2于点B3,过点B3作y轴的平行线交l1于点A3,连接A3B2与A2B3交于点C2,得到第2个△C2B2B3……按照此规律进行下去,则第2023个△C2022B2022B2023的面积是 .
三.解答题(共9小题,共102分)
17.(8分)先化简,再求值:(x﹣1+)÷,其中x为满足﹣3≤x≤﹣的整数解.
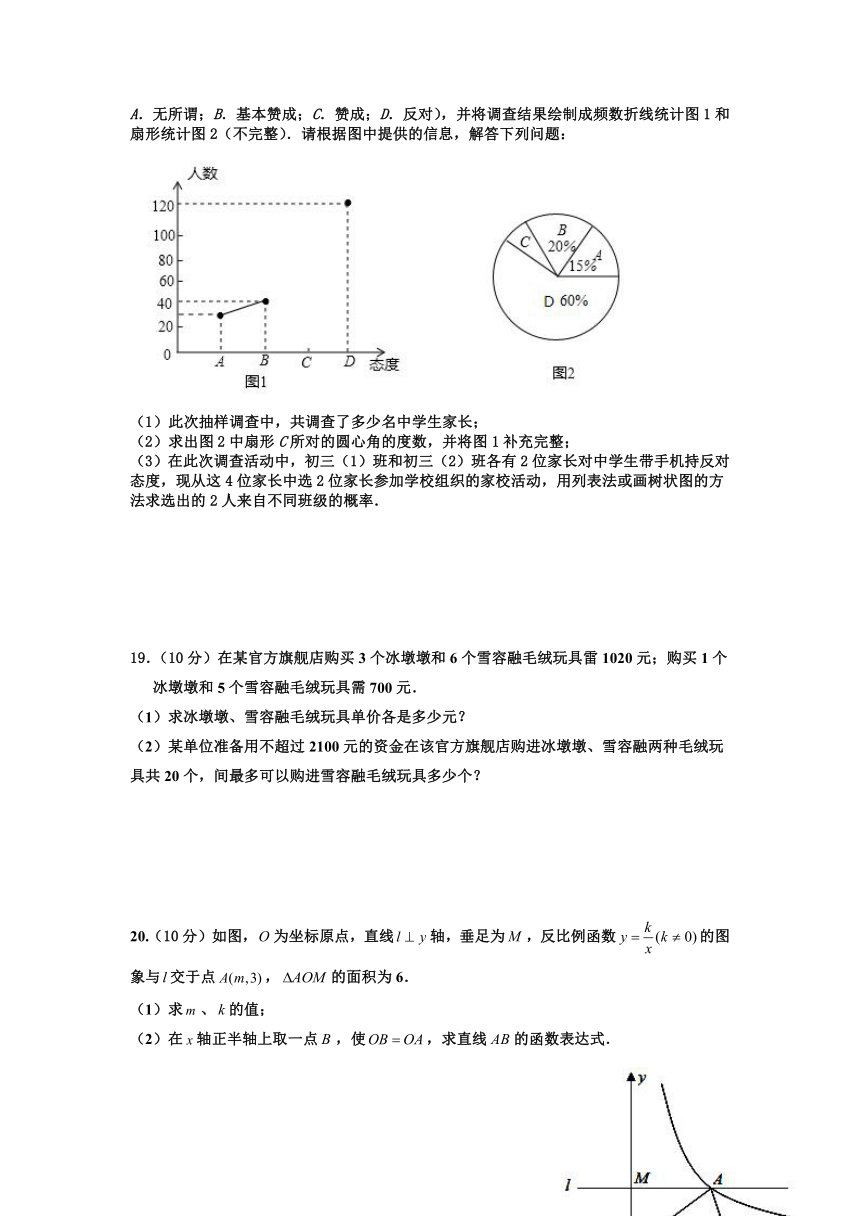
18.(12分)目前中学生带手机进校园现象越来越受到社会关注,针对这种现象,某校数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对),并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;
(3)在此次调查活动中,初三(1)班和初三(2)班各有2位家长对中学生带手机持反对态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求选出的2人来自不同班级的概率.
19.(10分)在某官方旗舰店购买3个冰墩墩和6个雪容融毛绒玩具雷1020元;购买1个冰墩墩和5个雪容融毛绒玩具需700元.
(1)求冰墩墩、雪容融毛绒玩具单价各是多少元?
(2)某单位准备用不超过2100元的资金在该官方旗舰店购进冰墩墩、雪容融两种毛绒玩具共20个,间最多可以购进雪容融毛绒玩具多少个?
20.(10分)如图,为坐标原点,直线轴,垂足为,反比例函数的图象与交于点,的面积为6.
(1)求、的值;
(2)在轴正半轴上取一点,使,求直线的函数表达式.
21.(12分)如图,AB为⊙O的直径,AC为弦,点D在⊙O外,
∠BCD=∠A,OD交⊙O于点E.
(1)求证:CD是⊙O的切线;
(2)若CD=4,AC=2.7,cos∠BCD=,求DE的长.
22.(12分)2020年是脱贫攻坚的收官之年,老李在驻村干部的帮助下,利用网络平台进行“直播带货”,销售一批成本为每件30元的商品,按单价不低于成本价,且不高于50元销售,经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间满足一次函数关系,
部分数据如表所示.
销售单价x(元) 30 40 45
销售数量y(件) 100 80 70
(1)求该商品每天的销售量y(件)与销售单价x(元)之间的函数关系式;
(2)销售单价定为多少元时,每天的销售利润为800元?
(3)销售单价定为多少元时,才能使销售该商品每天获得的利润w(元)最大?
最大利润是多少元?
23.(12分)如图,热气球的探测器显示,从热气球看一栋楼顶
部的仰角为30°,看这栋楼底的俯角为60°,热气球与楼的水
平距离为120米,求这栋楼的高度.
(结果精确到0.1米)(≈1.41,≈1.73)
24.(14分)如图1,在Rt△ABC中,∠ACB=90°,∠B=30°,点M是AB的中点,连接MC,点P是线段BC延长线上一点,且PC<BC,连接MP交AC于点H.将射线MP绕点M逆时针旋转60°交线段CA的延长线于点D.
(1)找出与∠AMP相等的角,并说明理由.
(2)如图2,CP=BC,求的值.
(3)在(2)的条件下,若MD=,求线段AB的长.
25.(14分)如图,直线y=﹣x+3与x轴交于点C,与y轴交于点B,经过B、C两点的
抛物线y=ax2+x+c与x轴的另一个交点为A.
(1)求抛物线的解析式;
(2)点E是直线BC上方抛物线上的一个动点,过点E作y轴的
平行线交直线BC于点M,当△BCE面积最大时,求出点M的坐标;
(3)在(2)的结论下,连接AM,点Q是抛物线对称轴上的动点,
在抛物线上是否存在点P,使得以P,Q,A,M为顶点的四边
形是平行四边形?如果存在,请直接写出点P的坐标:
如果不存在,请说明理由.
数学参考答案(三)
一、BCBBB CACCD
二、11.x≥﹣2 12. a(a﹣1)2 13. 4 14. 26° 15. 3.5 16.
三、17.,∵x+1≠0(x+2)(x﹣2)≠0,∴x≠﹣1,x≠±2,∵﹣3≤x≤﹣
∴x可以是﹣3,当x=﹣3时,原式==.
18.(1)200人 (2)18°, (3)
19.(1)冰墩墩毛绒玩具的单价是100元,雪容融毛绒玩具的单价是120元.
(2)最多可以购进雪容融毛绒玩具5个.
20.解:(1)由题意可得:,,即,,.
(2)轴,,.
设直线为,,解得:,..
21.(1)证明:如图,连接OC.∵AB为⊙O的直径,AC为弦,
∴∠ACB=90°,∠OCB+∠ACO=90°.∵OA=OC,∴∠ACO=∠A.
∵∠BCD=∠A,∴∠ACO=∠BCD.∴∠OCB+∠BCD=90°.
∴∠OCD=90°.∴CD⊥OC.∵OC为⊙O的半径,∴CD是⊙O的切线;
(2)解:∵∠BCD=∠A,cos∠BCD=,∴cosA=cos∠BCD=.
在Rt△ABC中,∠ACB=90°,AC=2.7,cosA=.∴AB===6.∴OC=OE==3.
在Rt△OCD中,∠OCD=90°,OC=3,CD=4,∴.∴DE=OD﹣OE=5﹣3=2.
22.解:(1)设该商品每天的销售量y(件)与销售单价x(元)之间的函数关系式为y=kx+b,
将点(3,100)、(40,80)代入一次函数关系式得:
,解得:.∴函数关系式为y=﹣2x+160;
(2)由题意得:(x﹣30)(﹣2x+160)=800,整理得:x2﹣110x+2800=0,解得:x1=40,x2=70.
∵单价不低于成本价,且不高于50元销售,∴x2=70不符合题意,舍去.
∴销售单价定为40元时,每天的销售利润为800元;
(3)由题意得:w=(x﹣30)(﹣2x+160)=﹣2(x﹣55)2+1250,∵﹣2<0,抛物线开口向下,
∴当x<55时,w随x的增大而增大,∵30≤x≤50,
∴当x=50时,w有最大值,此时w=﹣2(50﹣55)2+1250=1200.
∴销售单价定为50元时,才能使销售该商品每天获得的利润w(元)最大,最大利润是1200元.
23.解:如图,由题意可得,
∠BAD=30°,∠CAD=60°,AD=120米,∠ADC=∠ADB=90°,
在Rt△ADB中,∠BAD=30°,AD=120米,
∴BD=AD tan30°=120×=40(米),在Rt△ADC中,∠CAD=60°,AD=120米,
∴CD=AD tan60°=120(米),∴BC=BD+CD=40+120=160≈276.8(米),
即这栋楼的高度BC约为276.8米.
24.解:(1)∠D=∠AMP.理由如下:∵∠ACB=90°,∠B=30°,∴∠BAC=60°.∴∠D+∠DMA=60°.
由旋转的性质知,∠DMA+∠AMP=60°.∴∠D=∠AMP;
(2)如图,过点C作CG∥BA交MP于点G.∴∠GCP=∠B=30°,∠BCG=150°.
∵∠ACB=90°,点M是AB的中点,∴CM=AB=BM=AM.∴∠MCB=∠B=30°.∴∠MCG=120°.
∵∠MAD=180°﹣60°=120°.∴∠MAD=∠MCG.
∵∠DMG﹣∠AMG=∠AMC﹣∠AMG,∴∠DMA=∠GMC.
在△MDA与△MGC中,
∴△MDA≌△MGC(ASA).∴AD=CG.
∵CP=BC.∴CP=BP.∵CG∥BM,∴△CGP∽△BMP.
∴==.设CG=AD=t,则BM=3t,AB=6t.在Rt△ABC中,cosB==.
∴BC=3t.∴==;
(3)如图,由(2)知△CGP∽△BMP.则MD=MG=.∵CG∥MA.∴∠CGH=∠AMH.
∵∠GHC=∠MHA,∴△GHC∽△MHA.∴===.∴HG=MG=×=.
∴MH=﹣=.由(2)知,CG=AD=t,则BM=AM=CA=3t.
∴CH=t,AH=t.∵∠MHA=∠DHM,∠HMA=∠D.∴△MHA∽△DHM.∴=.
∴MH2=AH DH,即()2=tt.解得t1=,t2=﹣(舍去).∴AB=6t=2.
25.解:(1)令y=﹣x+3=0,则x=4,即点C(4,0),点B(0,3),则抛物线y=ax2+x+c=ax2+x+3,将点C坐标代入上式并解得:a=﹣,故抛物线的表达式为:y=﹣x2+x+3;
(2)设点E(x,﹣x2+x+3),则点M(x,﹣x+3),
S△BCE=EM×OC=2(﹣x2+x+3+x﹣3)=﹣x2+3x,
∵﹣<0,故S△BCE有最大值,此时x=2,故点M(2,);
(3)设点P(m,n),点Q(1,s),①当AM是平行四边形的一条边时,
当点P在对称轴的右侧时,点M向左平移4个单位向下平移个单位得到A,
同理P(m,n)向左平移4个单位向下平移个单位得到Q(1,s),
即m﹣4=1,解得:m=5,故点P(5,﹣);当点P在对称轴的左侧时,同理可得点P(﹣3,﹣);
②当AM是平行四边形的对角线时,AM的中点坐标为(0,),此坐标即为PQ的中点坐标,
即m+1=0,解得:m=﹣1,故点P(﹣1,);综上,点P(5,﹣)或(﹣3,﹣)或(﹣1,).
数 学 试 卷 满分150分
一、选择题(每小题3分,共30分)
1.﹣的相反数是( ) A.2 B. C.﹣2 D.﹣
2.每年的5月17日全国助残日,今年全国助残日的主题是“关注孤独症儿童,走向美好未来”.第二次全国残疾人抽样调查结果显示,我国0~6岁精神残疾儿童约为11.1万人.11.1万用科学记数法表示为( )
A.1.11×104 B.11.1×104 C.1.11×105 D.1.11×106
3.图所示的几何体的俯视图是( )
A. B. C. D.
4.下列运算正确的是( )
A.+= B.x8÷x2=x6 C.×= D.(a5)2=a7
第6题图 第8题图 第9题图
5.下列说法正确的是( )
A.一组数据2,2,3,4,这组数据的中位数是2
B.了解一批灯泡的使用寿命的情况,适合抽样调查
C.小明的三次数学成绩是126分,130分,136分,则小明这三次成绩的平均数是131分
D.某日最高气温是7℃,最低气温是﹣2℃,则该日气温的极差是5℃
6.如图,点E是 ABCD的边AD上的一点,且,连接BE并延长交CD的延长线于点F,若DE=3,DF=4,则 ABCD的周长为( )
A.21 B.28 C.34 D.42
7.随着5G网络技术的发展,市场对5G产品的需求越来越大,为满足市场需求,某大型5G产品生产厂家更新技术后,加快了生产速度,现在平均每天比更新技术前多生产30万件产品,现在生产500万件产品所需时间与更新技术前生产400万件产品所需时间相同.设更新技术前每天生产x万件产品,依题意得( )
A.= B.= C.= D.=
8.如图,已知⊙O的半径为2,△ABC内接于⊙O,∠ACB=135°,则AB=( )
A.4 B. C. D.
9.如图,在锐角三角形ABC中,BC=4,∠ABC=60°,BD平分∠ABC,交AC于点D,M,N分别是BD,BC上的动点,则CM+MN的最小值是( )
A. B.2 C.2 D.4
10.已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c<0;②a﹣b+c>1;③abc>0;④9a﹣3b+c<0;⑤c﹣a>1.其中所有正确结论的序号是( )
A.①② B.①③④ C.①②③④ D.①②③④⑤
第10题图 第14题图 第15题图 第16题图
二、填空题(每小题3分,共18分)
11.代数式在实数范围内有意义,则实数x的取值范围是 .
12.分解因式:a3﹣2a2+a= .
13.圆锥的底面半径为3,侧面积为12π,则这个圆锥的母线长为 .
14.在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是 ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的大小是 .
15.如图,点A是x轴负半轴上任意一点,过点A作y轴的平行线,分别与反比例函数y=﹣和y=的图象交于点B和C点,若D为y轴上任意一点,连接DC、DB,则△BCD的面积为 .
16.如图,在平面直角坐标系中,直线l1:y=x+与x轴交于点A1,与y轴交于点A2,过点A1作x轴的垂线交直线l2:y=x于点B1,过点A1作A1B1的垂线交y轴于点B2,此时点B2与原点O重合,连接A2B1交x轴于点C1,得到第1个△C1B1B2;过点A2作y轴的垂线交l2于点B3,过点B3作y轴的平行线交l1于点A3,连接A3B2与A2B3交于点C2,得到第2个△C2B2B3……按照此规律进行下去,则第2023个△C2022B2022B2023的面积是 .
三.解答题(共9小题,共102分)
17.(8分)先化简,再求值:(x﹣1+)÷,其中x为满足﹣3≤x≤﹣的整数解.
18.(12分)目前中学生带手机进校园现象越来越受到社会关注,针对这种现象,某校数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对),并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;
(3)在此次调查活动中,初三(1)班和初三(2)班各有2位家长对中学生带手机持反对态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求选出的2人来自不同班级的概率.
19.(10分)在某官方旗舰店购买3个冰墩墩和6个雪容融毛绒玩具雷1020元;购买1个冰墩墩和5个雪容融毛绒玩具需700元.
(1)求冰墩墩、雪容融毛绒玩具单价各是多少元?
(2)某单位准备用不超过2100元的资金在该官方旗舰店购进冰墩墩、雪容融两种毛绒玩具共20个,间最多可以购进雪容融毛绒玩具多少个?
20.(10分)如图,为坐标原点,直线轴,垂足为,反比例函数的图象与交于点,的面积为6.
(1)求、的值;
(2)在轴正半轴上取一点,使,求直线的函数表达式.
21.(12分)如图,AB为⊙O的直径,AC为弦,点D在⊙O外,
∠BCD=∠A,OD交⊙O于点E.
(1)求证:CD是⊙O的切线;
(2)若CD=4,AC=2.7,cos∠BCD=,求DE的长.
22.(12分)2020年是脱贫攻坚的收官之年,老李在驻村干部的帮助下,利用网络平台进行“直播带货”,销售一批成本为每件30元的商品,按单价不低于成本价,且不高于50元销售,经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间满足一次函数关系,
部分数据如表所示.
销售单价x(元) 30 40 45
销售数量y(件) 100 80 70
(1)求该商品每天的销售量y(件)与销售单价x(元)之间的函数关系式;
(2)销售单价定为多少元时,每天的销售利润为800元?
(3)销售单价定为多少元时,才能使销售该商品每天获得的利润w(元)最大?
最大利润是多少元?
23.(12分)如图,热气球的探测器显示,从热气球看一栋楼顶
部的仰角为30°,看这栋楼底的俯角为60°,热气球与楼的水
平距离为120米,求这栋楼的高度.
(结果精确到0.1米)(≈1.41,≈1.73)
24.(14分)如图1,在Rt△ABC中,∠ACB=90°,∠B=30°,点M是AB的中点,连接MC,点P是线段BC延长线上一点,且PC<BC,连接MP交AC于点H.将射线MP绕点M逆时针旋转60°交线段CA的延长线于点D.
(1)找出与∠AMP相等的角,并说明理由.
(2)如图2,CP=BC,求的值.
(3)在(2)的条件下,若MD=,求线段AB的长.
25.(14分)如图,直线y=﹣x+3与x轴交于点C,与y轴交于点B,经过B、C两点的
抛物线y=ax2+x+c与x轴的另一个交点为A.
(1)求抛物线的解析式;
(2)点E是直线BC上方抛物线上的一个动点,过点E作y轴的
平行线交直线BC于点M,当△BCE面积最大时,求出点M的坐标;
(3)在(2)的结论下,连接AM,点Q是抛物线对称轴上的动点,
在抛物线上是否存在点P,使得以P,Q,A,M为顶点的四边
形是平行四边形?如果存在,请直接写出点P的坐标:
如果不存在,请说明理由.
数学参考答案(三)
一、BCBBB CACCD
二、11.x≥﹣2 12. a(a﹣1)2 13. 4 14. 26° 15. 3.5 16.
三、17.,∵x+1≠0(x+2)(x﹣2)≠0,∴x≠﹣1,x≠±2,∵﹣3≤x≤﹣
∴x可以是﹣3,当x=﹣3时,原式==.
18.(1)200人 (2)18°, (3)
19.(1)冰墩墩毛绒玩具的单价是100元,雪容融毛绒玩具的单价是120元.
(2)最多可以购进雪容融毛绒玩具5个.
20.解:(1)由题意可得:,,即,,.
(2)轴,,.
设直线为,,解得:,..
21.(1)证明:如图,连接OC.∵AB为⊙O的直径,AC为弦,
∴∠ACB=90°,∠OCB+∠ACO=90°.∵OA=OC,∴∠ACO=∠A.
∵∠BCD=∠A,∴∠ACO=∠BCD.∴∠OCB+∠BCD=90°.
∴∠OCD=90°.∴CD⊥OC.∵OC为⊙O的半径,∴CD是⊙O的切线;
(2)解:∵∠BCD=∠A,cos∠BCD=,∴cosA=cos∠BCD=.
在Rt△ABC中,∠ACB=90°,AC=2.7,cosA=.∴AB===6.∴OC=OE==3.
在Rt△OCD中,∠OCD=90°,OC=3,CD=4,∴.∴DE=OD﹣OE=5﹣3=2.
22.解:(1)设该商品每天的销售量y(件)与销售单价x(元)之间的函数关系式为y=kx+b,
将点(3,100)、(40,80)代入一次函数关系式得:
,解得:.∴函数关系式为y=﹣2x+160;
(2)由题意得:(x﹣30)(﹣2x+160)=800,整理得:x2﹣110x+2800=0,解得:x1=40,x2=70.
∵单价不低于成本价,且不高于50元销售,∴x2=70不符合题意,舍去.
∴销售单价定为40元时,每天的销售利润为800元;
(3)由题意得:w=(x﹣30)(﹣2x+160)=﹣2(x﹣55)2+1250,∵﹣2<0,抛物线开口向下,
∴当x<55时,w随x的增大而增大,∵30≤x≤50,
∴当x=50时,w有最大值,此时w=﹣2(50﹣55)2+1250=1200.
∴销售单价定为50元时,才能使销售该商品每天获得的利润w(元)最大,最大利润是1200元.
23.解:如图,由题意可得,
∠BAD=30°,∠CAD=60°,AD=120米,∠ADC=∠ADB=90°,
在Rt△ADB中,∠BAD=30°,AD=120米,
∴BD=AD tan30°=120×=40(米),在Rt△ADC中,∠CAD=60°,AD=120米,
∴CD=AD tan60°=120(米),∴BC=BD+CD=40+120=160≈276.8(米),
即这栋楼的高度BC约为276.8米.
24.解:(1)∠D=∠AMP.理由如下:∵∠ACB=90°,∠B=30°,∴∠BAC=60°.∴∠D+∠DMA=60°.
由旋转的性质知,∠DMA+∠AMP=60°.∴∠D=∠AMP;
(2)如图,过点C作CG∥BA交MP于点G.∴∠GCP=∠B=30°,∠BCG=150°.
∵∠ACB=90°,点M是AB的中点,∴CM=AB=BM=AM.∴∠MCB=∠B=30°.∴∠MCG=120°.
∵∠MAD=180°﹣60°=120°.∴∠MAD=∠MCG.
∵∠DMG﹣∠AMG=∠AMC﹣∠AMG,∴∠DMA=∠GMC.
在△MDA与△MGC中,
∴△MDA≌△MGC(ASA).∴AD=CG.
∵CP=BC.∴CP=BP.∵CG∥BM,∴△CGP∽△BMP.
∴==.设CG=AD=t,则BM=3t,AB=6t.在Rt△ABC中,cosB==.
∴BC=3t.∴==;
(3)如图,由(2)知△CGP∽△BMP.则MD=MG=.∵CG∥MA.∴∠CGH=∠AMH.
∵∠GHC=∠MHA,∴△GHC∽△MHA.∴===.∴HG=MG=×=.
∴MH=﹣=.由(2)知,CG=AD=t,则BM=AM=CA=3t.
∴CH=t,AH=t.∵∠MHA=∠DHM,∠HMA=∠D.∴△MHA∽△DHM.∴=.
∴MH2=AH DH,即()2=tt.解得t1=,t2=﹣(舍去).∴AB=6t=2.
25.解:(1)令y=﹣x+3=0,则x=4,即点C(4,0),点B(0,3),则抛物线y=ax2+x+c=ax2+x+3,将点C坐标代入上式并解得:a=﹣,故抛物线的表达式为:y=﹣x2+x+3;
(2)设点E(x,﹣x2+x+3),则点M(x,﹣x+3),
S△BCE=EM×OC=2(﹣x2+x+3+x﹣3)=﹣x2+3x,
∵﹣<0,故S△BCE有最大值,此时x=2,故点M(2,);
(3)设点P(m,n),点Q(1,s),①当AM是平行四边形的一条边时,
当点P在对称轴的右侧时,点M向左平移4个单位向下平移个单位得到A,
同理P(m,n)向左平移4个单位向下平移个单位得到Q(1,s),
即m﹣4=1,解得:m=5,故点P(5,﹣);当点P在对称轴的左侧时,同理可得点P(﹣3,﹣);
②当AM是平行四边形的对角线时,AM的中点坐标为(0,),此坐标即为PQ的中点坐标,
即m+1=0,解得:m=﹣1,故点P(﹣1,);综上,点P(5,﹣)或(﹣3,﹣)或(﹣1,).
同课章节目录
