2023年初中学业水平考试数学适应性练习题八(含答案)
文档属性
| 名称 | 2023年初中学业水平考试数学适应性练习题八(含答案) | 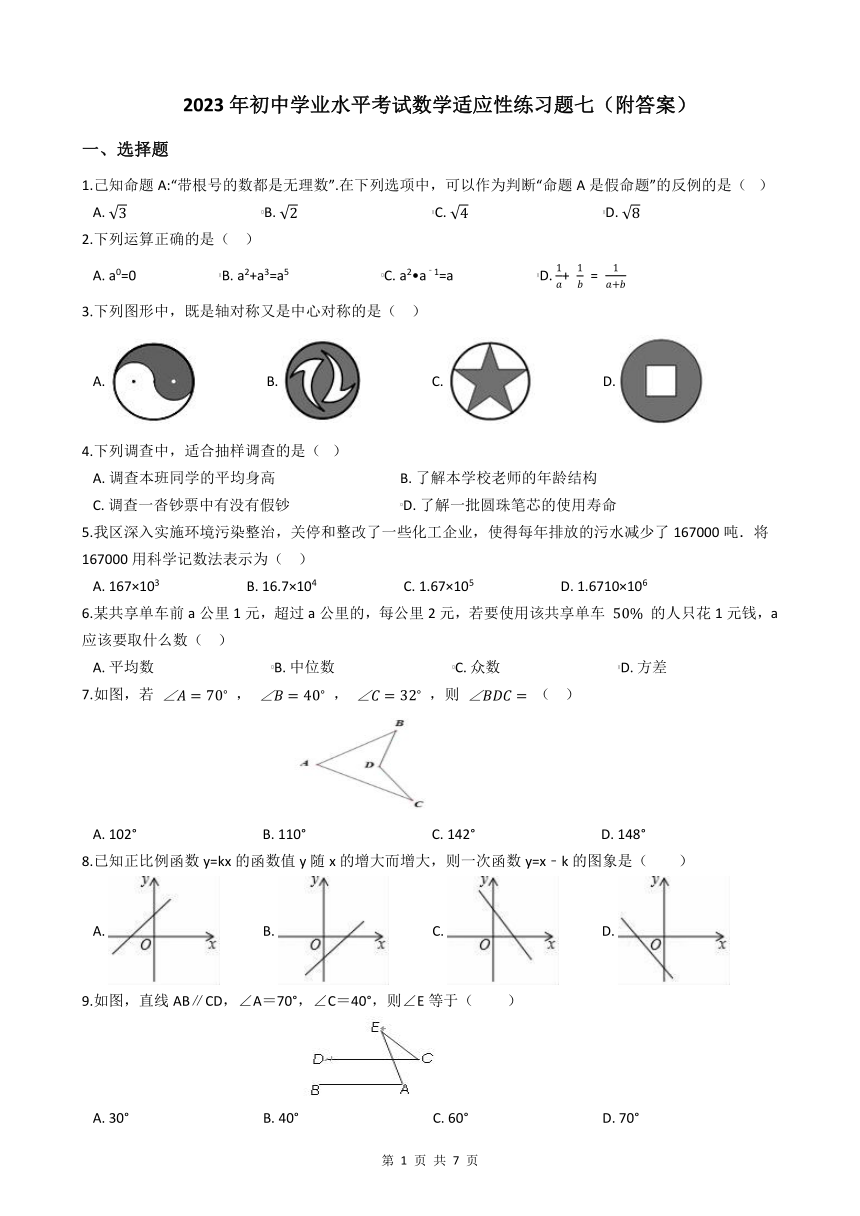 | |
| 格式 | docx | ||
| 文件大小 | 200.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-26 07:54:29 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
2023年初中学业水平考试数学适应性练习题七(附答案)
一、选择题
1.己知命题A:“带根号的数都是无理数”.在下列选项中,可以作为判断“命题A是假命题”的反例的是( )
A. B. C. D.
2.下列运算正确的是( )
A. a0=0 B. a2+a3=a5 C. a2 a﹣1=a D. + =
3.下列图形中,既是轴对称又是中心对称的是( )
A. B. C. D.
4.下列调查中,适合抽样调查的是( )
A. 调查本班同学的平均身高 B. 了解本学校老师的年龄结构
C. 调查一沓钞票中有没有假钞 D. 了解一批圆珠笔芯的使用寿命
5.我区深入实施环境污染整治,关停和整改了一些化工企业,使得每年排放的污水减少了167000吨.将167000用科学记数法表示为( )
A. 167×103 B. 16.7×104 C. 1.67×105 D. 1.6710×106
6.某共享单车前a公里1元,超过a公里的,每公里2元,若要使用该共享单车 的人只花1元钱,a应该要取什么数( )
A. 平均数 B. 中位数 C. 众数 D. 方差
7.如图,若 , , ,则 ( )
A. 102° B. 110° C. 142° D. 148°
8.已知正比例函数y=kx的函数值y随x的增大而增大,则一次函数y=x﹣k的图象是( )
A. B. C. D.
9.如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于( )
A. 30° B. 40° C. 60° D. 70°
10.如图,已知△ABC中,∠A=75°,则∠1+∠2=( )
A. 335°° B. 255° C. 155° D. 150°
11.某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需的时间与原计划生产450台机器所需时间相同.设原计划每天生产 台机器,则可列方程为
A. B. C. D.
12.某开发商的经适房的三个居民小区A、B、C在同一条直线上,位置如图所示.其中小区B到小区A、C的距离分别是70m和150m,现在想在小区A、C之间建立一个超市,要求各小区居民到超市总路程的和最小,那么超市的位置应建在( )
A. 小区A B. 小区B C. 小区C D. AC的中点
二、填空题
13.计算 =________
14.在平面直角坐标系中,O为坐标原点,点A(-a,a)(a>0),点B(-a-4,a+3),C为该直角坐标系内的一点,连结AB,OC.若AB//OC且AB=OC,则点C的坐标为________
15.如图, ,垂足为 ,过 作 .若 ,则 ________.
16.如图,七边形ABCDEFG中,AB,ED的延长线交于点O,若 , , , 的外角和等于 ,则 的度数为________.
17.已知圆锥的底面半径为40cm, 母线长为90cm, 则它的侧面展开图的圆心角为________.
18.已知线段AB=20, 点C是线段 上的黄金分割点(AC>BC),则 长是________(精确到0.01) .
三、综合题
19.(1)计算: ﹣2cos30°+|﹣ |.
(2)化简:a(3﹣a)+(a+1)(a﹣1).
20. (1)解方程组:
(2)解不等式组:
21.随着互联网、移动终端的迅速发展,数字化阅读越来越普及.公交、地铁上的“低头族”越来越多,某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(问卷训查表如下图所示),并将调查结果绘制成图①和图②所示的统计图(均不完整).
“您如何看待教化阅读”问卷调查表
您好!这是一份关于“您如何看待数字化间读问调查表,请在表格中选择一项您最认观点,在其后空格内打“√”,非常感谢您的合作.
代码 观点
A 获取信息方便,可以随时随地观看
B 价格便宜易得
C 使得人们成为“低头族”,不利于 人际交往
D 内容丰富,比低纸质书涉猎更广
E 其他
请根据统计图中提供的信息,解答下列问题:
(1)本次接受词查的总人数是________人,并将条形统计图补充完整________;
(2)在扇形统计图中,观点E的百分比是________,表示观点B的扇形的圆心角度数为________度.
(3)某市共有300万人,请根据以上调查结果估算该市持A、B、D观点赞成数字化阅读的人数共有多少万人.
22.某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD.瞭望台PC正前方水面上有两艘渔船M,N,观察员在瞭望台顶端P处观测渔船M的俯角α=31°,观测渔船N的俯角β=45°.已知MN所在直线与PC所在直线垂直,垂足为点E,PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米);
(2)已知坝高24米,坝长100米,背水坡AD的坡度i=1:0.25.为提高大坝防洪能力,某施工队在大坝的背水坡填筑土石加固,加固后坝顶加宽3米,背水坡FH的坡度为i=1:1.5.施工12天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的1.5倍,结果比原计划提前20天完成加固任务.施工队原计划平均每天填筑土石方多少立方米?(参考数据:tan31°≈0.60,sin31°≈0.52)
23.如图,在边长均为1的小正方形网格纸中,△OAB的顶点O,A,B均在格点上,且O是直角坐标系的原点,点A在x轴上.
(1)以O为位似中心,将△OAB放大,使得放大后的△OA1B1 , 与△OAB对应线段的比为2:1,画出△OA1B1 , (所画△OA1B1与△OAB在原点两侧);
(2)直接写出点A1、B1的坐标________;
(3)直接写出tan∠OA1B1 .
24.水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少2元,发现原来买这种水果80千克的钱,现在可买88千克.
(1)现在实际购进这种水果每千克多少元?
(2)王阿姨准备购进这种水果销售,若这种水果的销售量y(千克)与销售单价x(元/千克)满足如图所示的一次函数关系.
①求y与x之间的函数关系式;
②请你帮王阿姨拿个主意,将这种水果的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入﹣进货金额)
25.如图,反比例函数 ( ,)的图象与直线 相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
(1)求k的值;
(2)求点C的坐标;
(3)在y轴上确定一点M,使点M到C、D两点距离之和d=MC+MD最小,求点M的坐标.
26.如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AD=5,BE=3,求线段OE的长.
答案
一、选择题
1. C 2. C 3.D 4. D 5. C 6. B 7. C 8. B 9. A 10. B 11. C 12. B
二、填空题
13. 14. (-4,3),(4,-3) 15. 42° 16. 17. 18. 12.36
三、综合题
19. (1)解:原式=1﹣2× + =1
(2)解:a(3﹣a)+(a+1)(a﹣1) =3a﹣a2+a2﹣1=3a﹣1.
20. (1)解:解方程组 ②×2得 ③,①-③得 ,
,把 代入②得 ,方程组得解为 ;
(2)解:解不等式组 由①得 ,由②得 ,
不等式组的解集为 .
21. (1)5000;
(2)4%;18
(3)解:根据以上调查结果估算该市持A、B、D观点赞成数字化阅读的人数共有300× =198(万人)
22. (1)解:(1)在Rt△PEN中,∵∠PNE=45°,
∴EN=PE=30,
在Rt△PEM中,∠PME=31°,
tan∠PME= , ∴ME=≈50,∴MN=EM﹣EN=20;
(2)过点F作FM∥AD交AH于点M′,过点F作FN⊥AH交直线AH于点N′,
则四边形DFM′A为平行四边形,
∴∠FM′A=∠DAB,DF=AM=′3,
由题意得,tan∠FM′A=tan∠DAB=4,tan∠H= ,
在Rt△FN′H中,N′H==36,
在Rt△FN′M′中,M′N′==6,
∴HM′=30,AH=33,
梯形DAHF的面积为:×DN′×(DF+AH)=432,
所以需填土石方为432×100=43200,
设原计划平均每天填x立方米,由题意得,
12x+(﹣12﹣20)×1.5x=43200,
解得,x=600,
经检验x=600是方程的解,
原计划平均每天填筑土石方600立方米.
23. (1)解:如图2,△OA1B1即为所求;
(2)(4,0)和(2,﹣4)(3)解:2
24. (1)解:设现在实际购进这种水果每千克a元,则原来购进这种水果每千克(a+2)元,由题意,得
80(a+2)=88a,
解得a=20.
答:现在实际购进这种水果每千克20元;
(2)解:①设y与x之间的函数关系式为y=kx+b,
将(25,165),(35,55)代入,
得 ,解得 ,
故y与x之间的函数关系式为y=﹣11x+440;
②设这种水果的销售单价为x元时,所获利润为w元,
则w=(x﹣20)y=(x﹣20)(﹣11x+440)=﹣11x2+660x﹣8800=﹣11(x﹣30)2+1100,
所以当x=30时,w有最大值1100.
答:将这种水果的销售单价定为30元时,能获得最大利润,最大利润是1100元.
(1)解:A(1,3),∴AB=3,OB=1,∵AB=3BD,
∴BD=1,∴D(1,1)
将D坐标代入反比例解析式得:k=1;
(2)解:由(1)知,k=1,∴反比例函数的解析式为;y= ,解: ,
解得: 或 ,
∵x>0,∴C( , );
(3)解:如图,作C关于y轴的对称点C′,连接C′D交y轴于M,则d=MC+MD最小,∴C′(﹣ , ),
设直线C′D的解析式为:y=kx+b,
∴ ,∴ ,∴y=(﹣3+2 )x+2 ﹣2,
当x=0时,y=2 ﹣2, ∴M(0,2 ﹣2).
26. (1)证明:∵四边形ABCD为菱形, ∴AD∥BC,即AF∥EC,
∵CF∥AE,∴四边形AECF是平行四边形,
∵AE⊥BC,∴平行四边形AECF是矩形。
(2)解:∵四边形ABCD为菱形,四边形AECF为矩形,且BE=3,AD=5,
∴AB=BC=AD=5,DF=BE=3,∴AE= =4,
CE=BE+BC=8,
∴ ,
∵对角线AC,BD交于点O,∴OA=OC,
∵四边形AECF为矩形,∴点O是对角线AC与EF的交点,
∴ .
(
第
1
页 共
10
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
2023年初中学业水平考试数学适应性练习题七(附答案)
一、选择题
1.己知命题A:“带根号的数都是无理数”.在下列选项中,可以作为判断“命题A是假命题”的反例的是( )
A. B. C. D.
2.下列运算正确的是( )
A. a0=0 B. a2+a3=a5 C. a2 a﹣1=a D. + =
3.下列图形中,既是轴对称又是中心对称的是( )
A. B. C. D.
4.下列调查中,适合抽样调查的是( )
A. 调查本班同学的平均身高 B. 了解本学校老师的年龄结构
C. 调查一沓钞票中有没有假钞 D. 了解一批圆珠笔芯的使用寿命
5.我区深入实施环境污染整治,关停和整改了一些化工企业,使得每年排放的污水减少了167000吨.将167000用科学记数法表示为( )
A. 167×103 B. 16.7×104 C. 1.67×105 D. 1.6710×106
6.某共享单车前a公里1元,超过a公里的,每公里2元,若要使用该共享单车 的人只花1元钱,a应该要取什么数( )
A. 平均数 B. 中位数 C. 众数 D. 方差
7.如图,若 , , ,则 ( )
A. 102° B. 110° C. 142° D. 148°
8.已知正比例函数y=kx的函数值y随x的增大而增大,则一次函数y=x﹣k的图象是( )
A. B. C. D.
9.如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于( )
A. 30° B. 40° C. 60° D. 70°
10.如图,已知△ABC中,∠A=75°,则∠1+∠2=( )
A. 335°° B. 255° C. 155° D. 150°
11.某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需的时间与原计划生产450台机器所需时间相同.设原计划每天生产 台机器,则可列方程为
A. B. C. D.
12.某开发商的经适房的三个居民小区A、B、C在同一条直线上,位置如图所示.其中小区B到小区A、C的距离分别是70m和150m,现在想在小区A、C之间建立一个超市,要求各小区居民到超市总路程的和最小,那么超市的位置应建在( )
A. 小区A B. 小区B C. 小区C D. AC的中点
二、填空题
13.计算 =________
14.在平面直角坐标系中,O为坐标原点,点A(-a,a)(a>0),点B(-a-4,a+3),C为该直角坐标系内的一点,连结AB,OC.若AB//OC且AB=OC,则点C的坐标为________
15.如图, ,垂足为 ,过 作 .若 ,则 ________.
16.如图,七边形ABCDEFG中,AB,ED的延长线交于点O,若 , , , 的外角和等于 ,则 的度数为________.
17.已知圆锥的底面半径为40cm, 母线长为90cm, 则它的侧面展开图的圆心角为________.
18.已知线段AB=20, 点C是线段 上的黄金分割点(AC>BC),则 长是________(精确到0.01) .
三、综合题
19.(1)计算: ﹣2cos30°+|﹣ |.
(2)化简:a(3﹣a)+(a+1)(a﹣1).
20. (1)解方程组:
(2)解不等式组:
21.随着互联网、移动终端的迅速发展,数字化阅读越来越普及.公交、地铁上的“低头族”越来越多,某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(问卷训查表如下图所示),并将调查结果绘制成图①和图②所示的统计图(均不完整).
“您如何看待教化阅读”问卷调查表
您好!这是一份关于“您如何看待数字化间读问调查表,请在表格中选择一项您最认观点,在其后空格内打“√”,非常感谢您的合作.
代码 观点
A 获取信息方便,可以随时随地观看
B 价格便宜易得
C 使得人们成为“低头族”,不利于 人际交往
D 内容丰富,比低纸质书涉猎更广
E 其他
请根据统计图中提供的信息,解答下列问题:
(1)本次接受词查的总人数是________人,并将条形统计图补充完整________;
(2)在扇形统计图中,观点E的百分比是________,表示观点B的扇形的圆心角度数为________度.
(3)某市共有300万人,请根据以上调查结果估算该市持A、B、D观点赞成数字化阅读的人数共有多少万人.
22.某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD.瞭望台PC正前方水面上有两艘渔船M,N,观察员在瞭望台顶端P处观测渔船M的俯角α=31°,观测渔船N的俯角β=45°.已知MN所在直线与PC所在直线垂直,垂足为点E,PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米);
(2)已知坝高24米,坝长100米,背水坡AD的坡度i=1:0.25.为提高大坝防洪能力,某施工队在大坝的背水坡填筑土石加固,加固后坝顶加宽3米,背水坡FH的坡度为i=1:1.5.施工12天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的1.5倍,结果比原计划提前20天完成加固任务.施工队原计划平均每天填筑土石方多少立方米?(参考数据:tan31°≈0.60,sin31°≈0.52)
23.如图,在边长均为1的小正方形网格纸中,△OAB的顶点O,A,B均在格点上,且O是直角坐标系的原点,点A在x轴上.
(1)以O为位似中心,将△OAB放大,使得放大后的△OA1B1 , 与△OAB对应线段的比为2:1,画出△OA1B1 , (所画△OA1B1与△OAB在原点两侧);
(2)直接写出点A1、B1的坐标________;
(3)直接写出tan∠OA1B1 .
24.水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少2元,发现原来买这种水果80千克的钱,现在可买88千克.
(1)现在实际购进这种水果每千克多少元?
(2)王阿姨准备购进这种水果销售,若这种水果的销售量y(千克)与销售单价x(元/千克)满足如图所示的一次函数关系.
①求y与x之间的函数关系式;
②请你帮王阿姨拿个主意,将这种水果的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入﹣进货金额)
25.如图,反比例函数 ( ,)的图象与直线 相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
(1)求k的值;
(2)求点C的坐标;
(3)在y轴上确定一点M,使点M到C、D两点距离之和d=MC+MD最小,求点M的坐标.
26.如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AD=5,BE=3,求线段OE的长.
答案
一、选择题
1. C 2. C 3.D 4. D 5. C 6. B 7. C 8. B 9. A 10. B 11. C 12. B
二、填空题
13. 14. (-4,3),(4,-3) 15. 42° 16. 17. 18. 12.36
三、综合题
19. (1)解:原式=1﹣2× + =1
(2)解:a(3﹣a)+(a+1)(a﹣1) =3a﹣a2+a2﹣1=3a﹣1.
20. (1)解:解方程组 ②×2得 ③,①-③得 ,
,把 代入②得 ,方程组得解为 ;
(2)解:解不等式组 由①得 ,由②得 ,
不等式组的解集为 .
21. (1)5000;
(2)4%;18
(3)解:根据以上调查结果估算该市持A、B、D观点赞成数字化阅读的人数共有300× =198(万人)
22. (1)解:(1)在Rt△PEN中,∵∠PNE=45°,
∴EN=PE=30,
在Rt△PEM中,∠PME=31°,
tan∠PME= , ∴ME=≈50,∴MN=EM﹣EN=20;
(2)过点F作FM∥AD交AH于点M′,过点F作FN⊥AH交直线AH于点N′,
则四边形DFM′A为平行四边形,
∴∠FM′A=∠DAB,DF=AM=′3,
由题意得,tan∠FM′A=tan∠DAB=4,tan∠H= ,
在Rt△FN′H中,N′H==36,
在Rt△FN′M′中,M′N′==6,
∴HM′=30,AH=33,
梯形DAHF的面积为:×DN′×(DF+AH)=432,
所以需填土石方为432×100=43200,
设原计划平均每天填x立方米,由题意得,
12x+(﹣12﹣20)×1.5x=43200,
解得,x=600,
经检验x=600是方程的解,
原计划平均每天填筑土石方600立方米.
23. (1)解:如图2,△OA1B1即为所求;
(2)(4,0)和(2,﹣4)(3)解:2
24. (1)解:设现在实际购进这种水果每千克a元,则原来购进这种水果每千克(a+2)元,由题意,得
80(a+2)=88a,
解得a=20.
答:现在实际购进这种水果每千克20元;
(2)解:①设y与x之间的函数关系式为y=kx+b,
将(25,165),(35,55)代入,
得 ,解得 ,
故y与x之间的函数关系式为y=﹣11x+440;
②设这种水果的销售单价为x元时,所获利润为w元,
则w=(x﹣20)y=(x﹣20)(﹣11x+440)=﹣11x2+660x﹣8800=﹣11(x﹣30)2+1100,
所以当x=30时,w有最大值1100.
答:将这种水果的销售单价定为30元时,能获得最大利润,最大利润是1100元.
(1)解:A(1,3),∴AB=3,OB=1,∵AB=3BD,
∴BD=1,∴D(1,1)
将D坐标代入反比例解析式得:k=1;
(2)解:由(1)知,k=1,∴反比例函数的解析式为;y= ,解: ,
解得: 或 ,
∵x>0,∴C( , );
(3)解:如图,作C关于y轴的对称点C′,连接C′D交y轴于M,则d=MC+MD最小,∴C′(﹣ , ),
设直线C′D的解析式为:y=kx+b,
∴ ,∴ ,∴y=(﹣3+2 )x+2 ﹣2,
当x=0时,y=2 ﹣2, ∴M(0,2 ﹣2).
26. (1)证明:∵四边形ABCD为菱形, ∴AD∥BC,即AF∥EC,
∵CF∥AE,∴四边形AECF是平行四边形,
∵AE⊥BC,∴平行四边形AECF是矩形。
(2)解:∵四边形ABCD为菱形,四边形AECF为矩形,且BE=3,AD=5,
∴AB=BC=AD=5,DF=BE=3,∴AE= =4,
CE=BE+BC=8,
∴ ,
∵对角线AC,BD交于点O,∴OA=OC,
∵四边形AECF为矩形,∴点O是对角线AC与EF的交点,
∴ .
(
第
1
页 共
10
页
)
同课章节目录
