2023年初中学业水平考试数学适应性练习题六(含答案)
文档属性
| 名称 | 2023年初中学业水平考试数学适应性练习题六(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 224.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-26 08:02:44 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
2023年初中学业水平考试数学适应性练习题六(附答案)
一、选择题
1.在数0、1、-2、 、 中,最小的数是( )
A. 0 B. -2 C. ﹣ D. ﹣
2.下列运算正确的是( )
A. a3 a4=a12 B. m3+m4=m7 C. (a+b)2=a2+b2 D. n6÷n3=n3
3.要使代数式 有意义, 的取值范围是( )
A. B. C. D.
4.下列事件中,最适合采用普查的是( )
A. 了解一批灯泡的使用寿命 B. 了解中央电视台《最强大脑》栏目的收视率
C. 了解全国中学生体重情况 D. 了解某班学生对“社会主义核心价值观”的知晓率
5.如图是由5个大小相同的正方体组成的几何体,则该几何体的主视图是( )
A. B. C. D.
6.如图,在△ABC中,∠C=90°,∠B=26°.洋洋按下列步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于EF长的一半为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D,则∠ADC的度数为( )
A. 50° B. 52° C. 58° D. 64°
7.已知直线y=kx+b(k≠0)与x轴的交点在x轴的正半轴,下列结论:①k>0,b>0;②k>0,b<0;③k<0,b>0;④k<0,b<0.其中正确的结论的个数是( )
A. 1 B. 2 C. 3 D. 4
8.对抛物线:y=-x2+2x-3而言,下列结论正确的是( )
A. 与x轴有两个交点 B. 开口向上 C. 与y轴交点坐标是(0,3) D. 顶点坐标是(1,-2)
二、填空题
9.计算: ________.
10.把多项式 分解因式的结果是________.
11.据黄石市文化和旅游局统计,2019年中秋节期间,我市共接待游客 万人次,实现旅游收入 元,将 科学记数法表示为________.
12.已知坐标平面内一点A(1,-2)
若A、B两点关于x轴对称,则B(________),
若A、B两点关于y轴对称,则B(________),
若A、B两点关于原点对称,则B(________).
13.如图在△ABC中,点D、E分别在AB、AC上,且DE∥BC,已知AD=2,DB=4,AC=4.5,则EC=________.
14.矩形ABCD的两条对角线相交于O , ∠AOB=60°,AB=8,则矩形对角线的长________.
15.如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2 , 使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3 , 使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是________.
16.不等式组 的整数解________.
17.已知等腰三角形的一个角为42°,则它的底角度数为________.
18.如图,在锐角三角形ABC中, , ,点D为边AB的中点,点E在边AC上,将 沿DE折叠得到 .若 ,则 的值为________; 的值为________.
三、解答题
19.计算:
(1)
(2)
20.先化简,再求值: ,其中x=2 ﹣1.
21.在一个不透明的盒子中装有6张卡片,6张卡片的正面分别标有数字﹣4,﹣3,﹣2,﹣1,6,8,这些卡片除数字外都相同,将卡片搅匀.
(1)从盒子中任意抽取一张卡片,求恰好抽到标有偶数卡片的概率;
(2)先从盒子中任意抽取一张卡片,把它上面的数字作为一个点的横坐标,不放回,再从盒子剩余的卡片中任意抽取一张卡片,把它上面的数字作为这个点的纵坐标,求抽取的点恰好落在第二象限的概率.
22.小明随机调查了若干市民租用共享单车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如下统计图(A:0<t≤10,B:10<t≤20,C:20<t≤30,D:t>30),根据图中信息,解答下列问题:
(1)这项被调查的总人数是多少人?
(2)试求表示A组的扇形统计图的圆心角的度数,补全条形统计图;
(3)如果小明想从D组的甲、乙、丙、丁四人中随机选择两人了解平时租用共享单车情况,请用列表或画树状图的方法求出恰好选中甲的概率.
23.某校准备购买一批学习用品作为奖品奖励优秀学生,已知买2本笔记本和1本练习本需要18元,买1本笔记本和2本练习本需要12元.
(1)求购买1本笔记本,1本练习本各需要多少元;
(2)现学校决定用不超过1200元,购买笔记本和练习本共300本,问最多能购买笔记本多少本?
24.一个分数的分母比它的分子大5,如果将这个分数的分子加上14,分母减去1,那么所得分数是原分数的倒数,求原分数.
25.已知,在△ABC中,∠A=90°,AB=AC,D为BC的中点,E,F分别是AB,AC上的点,且BE=AF.
(1)请你判断△DEF形状,并说明理由;
(2)若BE=2cm,CF=4cm,求EF的长.
26.已知:如图, 为圆 的直径,点 、 在圆 上,且 , , .
(1)求 的长;
(2)求图中阴影部分(弦 和其所对劣弧围成的图形)的面积
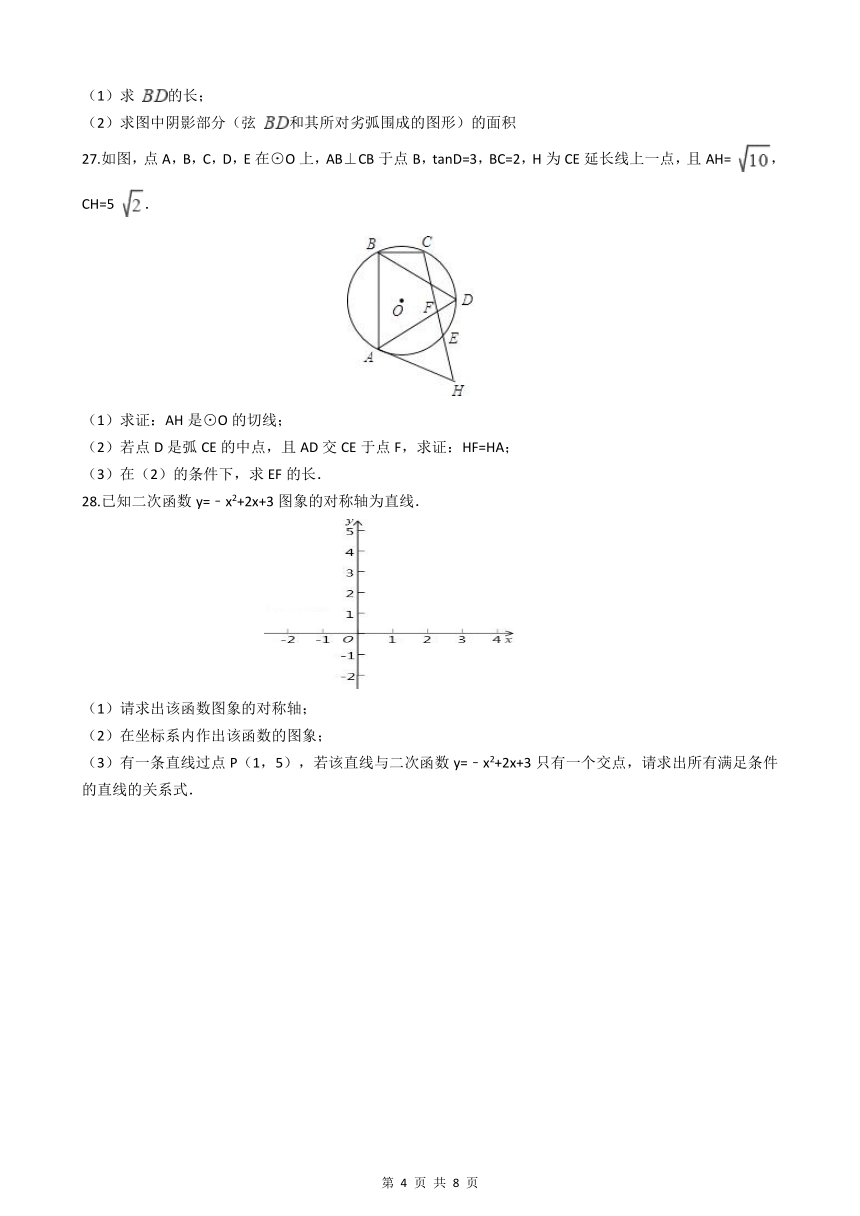
27.如图,点A,B,C,D,E在⊙O上,AB⊥CB于点B,tanD=3,BC=2,H为CE延长线上一点,且AH= ,CH=5 .
(1)求证:AH是⊙O的切线;
(2)若点D是弧CE的中点,且AD交CE于点F,求证:HF=HA;
(3)在(2)的条件下,求EF的长.
28.已知二次函数y=﹣x2+2x+3图象的对称轴为直线.
(1)请求出该函数图象的对称轴;
(2)在坐标系内作出该函数的图象;
(3)有一条直线过点P(1,5),若该直线与二次函数y=﹣x2+2x+3只有一个交点,请求出所有满足条件的直线的关系式.
答 案
一、选择题
1. B 2.D 3. D 4. D 5. D 6. C 7. B 8. D
二、填空题
9. 10. y(x+2)(x﹣2) 11. 12. 1,2;-1,-2;-1,2 13. 3
14.16 15.( ) n﹣1×75° 16. ﹣1,0,1 17. 42°或69° 18. ;
三、解答题
19. (1)解:原式=3 +4+1-5=3 ;
(2)解:原式= = =
20. 解: = = ,
把x=2 -1代入得,原式= =
21. (1)解:6张卡片中,偶数卡片有-4,-2, 6,8共4张,
∴恰好抽到标有偶数卡片的概率为 ;
(2)解:列表如下:
-4 -3 -2 -1 6 8
-4 (-3,-4) (-2,-4) (-1,-4) (6,-4) (8,-4)
-3 (-4,-3) (-2,-3) (-1,-3) (6,-3) (8,-3)
-2 (-4,-2) (-3,-2) (-1,-2) (6,-2) (8,-2)
-1 (-4,-1) (-3,-1) (-2,-1) (6,-1) (8,-1)
6 (-4,6) (-3,6) (-2,6) (-1,6) (8,6)
8 (-4,8) (-3,8) (-2,8) (-1,8) (6,8)
由表可知共有30种等可能结果,其中落在第二象限的有8种结果,
∴抽取的点恰好落在第二象限的概率为 .
22. (1)调查的总人数是:19÷38%=50(人)
(2)A组所占圆心角的度数是:360°× =108°;
C组的人数有:50﹣15﹣19﹣4=12(人),
补全条形图如图所示:
(3)画树状图,共有12个可能的结果,
恰好选中甲的结果有6个,
∴P(恰好选中甲)= = .
23. (1)解:设购买1本笔记本需要x元,1本练习本需要y元,由题意得:
,解得:
(2)解:设购买笔记为a本,则购买练习本为(300-a)本,根据题意可得:
解得:
答:最多能购买笔记本100本
24.解:设原分数的分子为x,则分母为x+5. 根据题意,得 ,
解得 x=4. 经检验,x=4是所列方程的解.
答:原分数为
25. (1)解:△DEF是等腰直角三角形.
如图,连接AD,
∵AB=AC,∠BAC=90°,D为BC中点,
∴AD= BC=BD=CD,且AD平分∠BAC,
∴∠BAD=∠CAD=45°,
在△BDE和△ADF中,
,
∴△BDE≌△ADF(SAS),
∴DE=DF,∠BDE=∠ADF,
∵∠BDE+∠ADE=90°,∴∠ADF+∠ADE=90°,即∠EDF=90°,
∴△EDF为等腰直角三角形.
(2)解:如图,延长ED至G,使得DG=DE,连接FG,CG,
∵D为BC的中点,∴BD=CD,
又∵∠BDE=∠CDG,∴△BDE≌△CDG,
∴CG=BE=2cm,∠B=∠DCG=45°=∠ACB,
∴∠GCF=90°,
又∵CF=4cm,
∴Rt△CFG中,FG= = =2 cm,
∵∠EDF=90°,ED=GD,
∴FD垂直平分EG,∴EF=GF=2 cm.
26. (1)解:∵AB为⊙O的直径, ∴∠ACB=90°,
∵BC=6cm,AC=8cm,∴AB=10cm.∴OB=5cm.
连OD,
∵OD=OB,∴∠ODB=∠ABD=45°.
∴∠BOD=90°.
∴BD= =5 cm
(2)解:S阴影=S扇形-S△OBD= - = cm2.
27. (1)证明:如图1所示:连接AC.
∵AB⊥CB,∴AC是圆O的直径.
∵∠C=∠D,∴tanC=3.
∴AB=3BC=3×2=6.
在Rt△ABC中,由勾股定理得:AC2=AB2+BC2=40.
又∵AH2=10,CH2=50,∴AC2+AH2=CH2 .
∴△ACH为直角三角形.∴AC⊥AH.
∴AH是圆O的切线.
(2)解:如图2所示:连接DE、BE.
∵AH是圆O的切线,∴∠ABD=∠HAD.
∵D是 的中点,
∴ .∴∠CED=∠EBD.
又∵∠ABE=∠ADE,
∴∠ABE+∠EBD=∠ADE+∠CED.∴∠ABD=∠AFE.
∴∠HAF=∠AFH.
∴AH=HF.
(3)解:由切割线定理可知:AH2=EH CH,即( )2=5 EH.
解得:EH= .
∵由(2)可知AF=FH= .∴EF=FH﹣EH= .
28. (1)解:
(2)解:图象
(3)解:因为抛物线的对称轴是x=1,点p(1,5)
当过点p且与y轴平行的直线满足与抛物线只有一个交点
所以直线x=1为所求直线
当过点p的直线不与y轴平行时,设直线的解析式为y=kx+b,
令﹣x2+2x+3=kx+b
整理得﹣x2+(2﹣k)x+3﹣b=0由题意得△=(2﹣k)2+4(3﹣b)=0
即:k2﹣4k+16﹣4b=0
又因为y=kx+b,过点p(1,5)所以5=k+b
所以k2﹣4=0解得k=±2,
当k=2时,b=3;当k=﹣2时,b=7
所以解析式为y1=2x+3,y2=﹣2x+7,
所以满足条件的直线有三条:直线x=1;y1=2x+3,y2=﹣2x+7.
(
第
- 1 -
页 共
12
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
2023年初中学业水平考试数学适应性练习题六(附答案)
一、选择题
1.在数0、1、-2、 、 中,最小的数是( )
A. 0 B. -2 C. ﹣ D. ﹣
2.下列运算正确的是( )
A. a3 a4=a12 B. m3+m4=m7 C. (a+b)2=a2+b2 D. n6÷n3=n3
3.要使代数式 有意义, 的取值范围是( )
A. B. C. D.
4.下列事件中,最适合采用普查的是( )
A. 了解一批灯泡的使用寿命 B. 了解中央电视台《最强大脑》栏目的收视率
C. 了解全国中学生体重情况 D. 了解某班学生对“社会主义核心价值观”的知晓率
5.如图是由5个大小相同的正方体组成的几何体,则该几何体的主视图是( )
A. B. C. D.
6.如图,在△ABC中,∠C=90°,∠B=26°.洋洋按下列步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于EF长的一半为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D,则∠ADC的度数为( )
A. 50° B. 52° C. 58° D. 64°
7.已知直线y=kx+b(k≠0)与x轴的交点在x轴的正半轴,下列结论:①k>0,b>0;②k>0,b<0;③k<0,b>0;④k<0,b<0.其中正确的结论的个数是( )
A. 1 B. 2 C. 3 D. 4
8.对抛物线:y=-x2+2x-3而言,下列结论正确的是( )
A. 与x轴有两个交点 B. 开口向上 C. 与y轴交点坐标是(0,3) D. 顶点坐标是(1,-2)
二、填空题
9.计算: ________.
10.把多项式 分解因式的结果是________.
11.据黄石市文化和旅游局统计,2019年中秋节期间,我市共接待游客 万人次,实现旅游收入 元,将 科学记数法表示为________.
12.已知坐标平面内一点A(1,-2)
若A、B两点关于x轴对称,则B(________),
若A、B两点关于y轴对称,则B(________),
若A、B两点关于原点对称,则B(________).
13.如图在△ABC中,点D、E分别在AB、AC上,且DE∥BC,已知AD=2,DB=4,AC=4.5,则EC=________.
14.矩形ABCD的两条对角线相交于O , ∠AOB=60°,AB=8,则矩形对角线的长________.
15.如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2 , 使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3 , 使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是________.
16.不等式组 的整数解________.
17.已知等腰三角形的一个角为42°,则它的底角度数为________.
18.如图,在锐角三角形ABC中, , ,点D为边AB的中点,点E在边AC上,将 沿DE折叠得到 .若 ,则 的值为________; 的值为________.
三、解答题
19.计算:
(1)
(2)
20.先化简,再求值: ,其中x=2 ﹣1.
21.在一个不透明的盒子中装有6张卡片,6张卡片的正面分别标有数字﹣4,﹣3,﹣2,﹣1,6,8,这些卡片除数字外都相同,将卡片搅匀.
(1)从盒子中任意抽取一张卡片,求恰好抽到标有偶数卡片的概率;
(2)先从盒子中任意抽取一张卡片,把它上面的数字作为一个点的横坐标,不放回,再从盒子剩余的卡片中任意抽取一张卡片,把它上面的数字作为这个点的纵坐标,求抽取的点恰好落在第二象限的概率.
22.小明随机调查了若干市民租用共享单车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如下统计图(A:0<t≤10,B:10<t≤20,C:20<t≤30,D:t>30),根据图中信息,解答下列问题:
(1)这项被调查的总人数是多少人?
(2)试求表示A组的扇形统计图的圆心角的度数,补全条形统计图;
(3)如果小明想从D组的甲、乙、丙、丁四人中随机选择两人了解平时租用共享单车情况,请用列表或画树状图的方法求出恰好选中甲的概率.
23.某校准备购买一批学习用品作为奖品奖励优秀学生,已知买2本笔记本和1本练习本需要18元,买1本笔记本和2本练习本需要12元.
(1)求购买1本笔记本,1本练习本各需要多少元;
(2)现学校决定用不超过1200元,购买笔记本和练习本共300本,问最多能购买笔记本多少本?
24.一个分数的分母比它的分子大5,如果将这个分数的分子加上14,分母减去1,那么所得分数是原分数的倒数,求原分数.
25.已知,在△ABC中,∠A=90°,AB=AC,D为BC的中点,E,F分别是AB,AC上的点,且BE=AF.
(1)请你判断△DEF形状,并说明理由;
(2)若BE=2cm,CF=4cm,求EF的长.
26.已知:如图, 为圆 的直径,点 、 在圆 上,且 , , .
(1)求 的长;
(2)求图中阴影部分(弦 和其所对劣弧围成的图形)的面积
27.如图,点A,B,C,D,E在⊙O上,AB⊥CB于点B,tanD=3,BC=2,H为CE延长线上一点,且AH= ,CH=5 .
(1)求证:AH是⊙O的切线;
(2)若点D是弧CE的中点,且AD交CE于点F,求证:HF=HA;
(3)在(2)的条件下,求EF的长.
28.已知二次函数y=﹣x2+2x+3图象的对称轴为直线.
(1)请求出该函数图象的对称轴;
(2)在坐标系内作出该函数的图象;
(3)有一条直线过点P(1,5),若该直线与二次函数y=﹣x2+2x+3只有一个交点,请求出所有满足条件的直线的关系式.
答 案
一、选择题
1. B 2.D 3. D 4. D 5. D 6. C 7. B 8. D
二、填空题
9. 10. y(x+2)(x﹣2) 11. 12. 1,2;-1,-2;-1,2 13. 3
14.16 15.( ) n﹣1×75° 16. ﹣1,0,1 17. 42°或69° 18. ;
三、解答题
19. (1)解:原式=3 +4+1-5=3 ;
(2)解:原式= = =
20. 解: = = ,
把x=2 -1代入得,原式= =
21. (1)解:6张卡片中,偶数卡片有-4,-2, 6,8共4张,
∴恰好抽到标有偶数卡片的概率为 ;
(2)解:列表如下:
-4 -3 -2 -1 6 8
-4 (-3,-4) (-2,-4) (-1,-4) (6,-4) (8,-4)
-3 (-4,-3) (-2,-3) (-1,-3) (6,-3) (8,-3)
-2 (-4,-2) (-3,-2) (-1,-2) (6,-2) (8,-2)
-1 (-4,-1) (-3,-1) (-2,-1) (6,-1) (8,-1)
6 (-4,6) (-3,6) (-2,6) (-1,6) (8,6)
8 (-4,8) (-3,8) (-2,8) (-1,8) (6,8)
由表可知共有30种等可能结果,其中落在第二象限的有8种结果,
∴抽取的点恰好落在第二象限的概率为 .
22. (1)调查的总人数是:19÷38%=50(人)
(2)A组所占圆心角的度数是:360°× =108°;
C组的人数有:50﹣15﹣19﹣4=12(人),
补全条形图如图所示:
(3)画树状图,共有12个可能的结果,
恰好选中甲的结果有6个,
∴P(恰好选中甲)= = .
23. (1)解:设购买1本笔记本需要x元,1本练习本需要y元,由题意得:
,解得:
(2)解:设购买笔记为a本,则购买练习本为(300-a)本,根据题意可得:
解得:
答:最多能购买笔记本100本
24.解:设原分数的分子为x,则分母为x+5. 根据题意,得 ,
解得 x=4. 经检验,x=4是所列方程的解.
答:原分数为
25. (1)解:△DEF是等腰直角三角形.
如图,连接AD,
∵AB=AC,∠BAC=90°,D为BC中点,
∴AD= BC=BD=CD,且AD平分∠BAC,
∴∠BAD=∠CAD=45°,
在△BDE和△ADF中,
,
∴△BDE≌△ADF(SAS),
∴DE=DF,∠BDE=∠ADF,
∵∠BDE+∠ADE=90°,∴∠ADF+∠ADE=90°,即∠EDF=90°,
∴△EDF为等腰直角三角形.
(2)解:如图,延长ED至G,使得DG=DE,连接FG,CG,
∵D为BC的中点,∴BD=CD,
又∵∠BDE=∠CDG,∴△BDE≌△CDG,
∴CG=BE=2cm,∠B=∠DCG=45°=∠ACB,
∴∠GCF=90°,
又∵CF=4cm,
∴Rt△CFG中,FG= = =2 cm,
∵∠EDF=90°,ED=GD,
∴FD垂直平分EG,∴EF=GF=2 cm.
26. (1)解:∵AB为⊙O的直径, ∴∠ACB=90°,
∵BC=6cm,AC=8cm,∴AB=10cm.∴OB=5cm.
连OD,
∵OD=OB,∴∠ODB=∠ABD=45°.
∴∠BOD=90°.
∴BD= =5 cm
(2)解:S阴影=S扇形-S△OBD= - = cm2.
27. (1)证明:如图1所示:连接AC.
∵AB⊥CB,∴AC是圆O的直径.
∵∠C=∠D,∴tanC=3.
∴AB=3BC=3×2=6.
在Rt△ABC中,由勾股定理得:AC2=AB2+BC2=40.
又∵AH2=10,CH2=50,∴AC2+AH2=CH2 .
∴△ACH为直角三角形.∴AC⊥AH.
∴AH是圆O的切线.
(2)解:如图2所示:连接DE、BE.
∵AH是圆O的切线,∴∠ABD=∠HAD.
∵D是 的中点,
∴ .∴∠CED=∠EBD.
又∵∠ABE=∠ADE,
∴∠ABE+∠EBD=∠ADE+∠CED.∴∠ABD=∠AFE.
∴∠HAF=∠AFH.
∴AH=HF.
(3)解:由切割线定理可知:AH2=EH CH,即( )2=5 EH.
解得:EH= .
∵由(2)可知AF=FH= .∴EF=FH﹣EH= .
28. (1)解:
(2)解:图象
(3)解:因为抛物线的对称轴是x=1,点p(1,5)
当过点p且与y轴平行的直线满足与抛物线只有一个交点
所以直线x=1为所求直线
当过点p的直线不与y轴平行时,设直线的解析式为y=kx+b,
令﹣x2+2x+3=kx+b
整理得﹣x2+(2﹣k)x+3﹣b=0由题意得△=(2﹣k)2+4(3﹣b)=0
即:k2﹣4k+16﹣4b=0
又因为y=kx+b,过点p(1,5)所以5=k+b
所以k2﹣4=0解得k=±2,
当k=2时,b=3;当k=﹣2时,b=7
所以解析式为y1=2x+3,y2=﹣2x+7,
所以满足条件的直线有三条:直线x=1;y1=2x+3,y2=﹣2x+7.
(
第
- 1 -
页 共
12
页
)
同课章节目录
