课题学习[下学期]

课件25张PPT。九年级数学(上)第五章 反比例函数5.课题学习猜想,证明与拓广数学很神奇 世界三大几何难题平面几何作图限制只能用直尺、圆规,而这里所谓的直尺是指没有刻度只能画直线的尺.用直尺与圆规当然可以做出许多种之图形,但有些图形如正七边形、正九边形就做不出来.有些问题看起来好像很简单,但真正做出来却很困难,这些问题之中最有名的就是所谓的三大问题. 世界三大几何难题化圆为方——求作一正方形使其面积等于一已知圆的面积.圆与正方形都是常见的几何图形，但如何作一个正方形和已知圆等面积呢？
化圆为方世界三大几何难题对于某些角如900、1800三等分并不难,但是否所有角都可以三等分呢？例如600,若能三等分则可以做出200的角,那么正18边形及正九边形也都可以做出来了（注：圆内接一正十八边形每一边所对的圆周角为3600/18=200）.三等分任意角 世界三大几何难题倍立方倍立方——求作一立方体使其体积是一已知立方体的二倍 挑战“自我”猜想,证明与拓广1.任意给定一个正方形,是否存在另一个正方形,它的周长和面积分别是已知正方形周长和面积的2倍?2.你准备怎么去做?
3.你是怎么做的?
4.你有哪些解决方法?
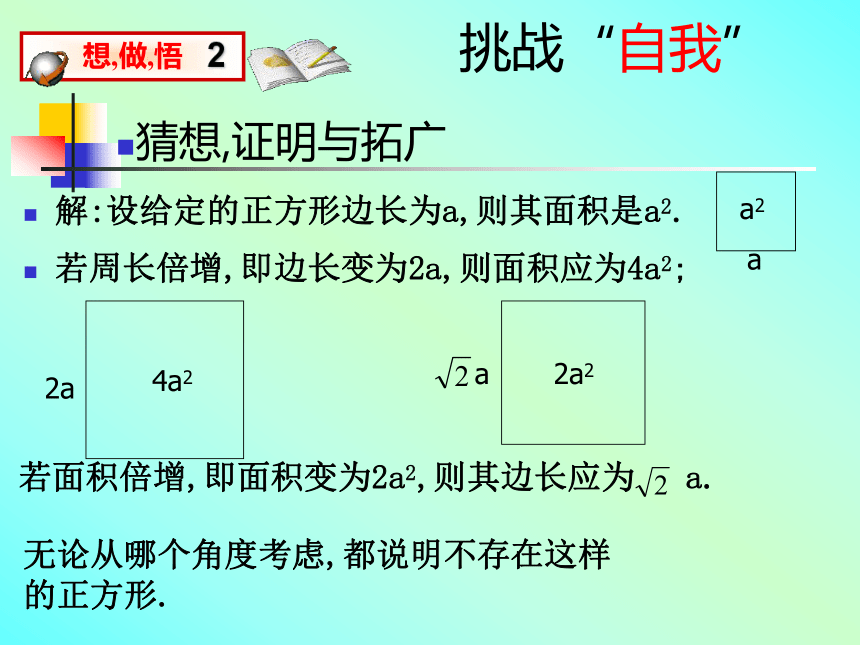
5.你提出新的问题吗?挑战“自我”解:设给定的正方形边长为a,则其面积是a2.猜想,证明与拓广若周长倍增,即边长变为2a,则面积应为4a2;无论从哪个角度考虑,都说明不存在这样的正方形.挑战“自我”猜想,证明与拓广任意给定一个矩形,是否存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍?老师提示:
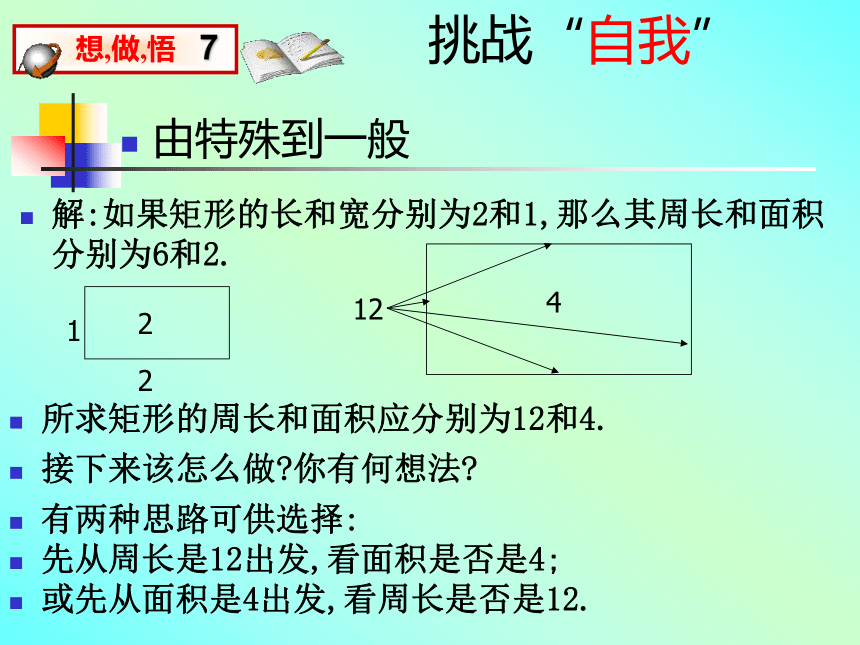
矩形的形状太多了我们可以先研究一个具体的矩形,比如长和宽分别为2和1,怎么样?挑战“自我”由特殊到一般解:如果矩形的长和宽分别为2和1,那么其周长和面积分别为6和2.所求矩形的周长和面积应分别为12和4.接下来该怎么做?你有何想法?有两种思路可供选择:
先从周长是12出发,看面积是否是4;
或先从面积是4出发,看周长是否是12.挑战“自我”(1)从周长是12出发,看面积是否是4;
如果设所求矩形的长为x,那么它宽为6-x,其面积为x(6-x).根据题意,得
x(6-x)=4.
即 x2-6x+4=0.
如果这个方程有解,则说明这样的矩形存在.
解这个方程得:猜想,证明与拓广结论:如果矩形的长和宽分别为2和1,那么存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍.挑战“自我”(2)从面积是4出发,看周长是否是12.
解:如果设所求矩形的长为x,那么宽为4/x,其周长为2(x+4/x).根据题意,得
x+4/x=6.
即 x2-6x+4=0.
显然这个方程有解,由此说明这样的矩形存在.
解这个方程得:猜想,证明与拓广结论:如果矩形的长和宽分别为2和1,那么存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍.挑战“自我”由特殊到一般如果已知矩形的长和宽分别为3和1,是否还有相同的结论?
如果已知矩形的长和宽分别为4和1,5和1,……,n和1呢?
更一般地,当已知矩形的长和宽分别为m和n时,是否仍然有相同的结论?
还等什么！用实际行动证明:第一个得到结论的是我!由特殊到一般挑战“自我”分析:如果矩形的长和宽分别为m和n,那么其周长和面积分别为2(m+n)和mn,所求矩形的周长和面积应分别为4(m+n)和2mn.
从周长是4(m+n)出发,看面积是否是2mn;
解:如果设所求矩形的长为x,那么它宽为2(m+n)-x,其面积为x[2(m+n)-x].根据题意,得
x[2(m+n)-x]=2mn.
即 x2-2(m+n)x+2mn=0.
解这个方程得:若从面积是2mn出发,可得同样的结论.挑战“自我”结论:任意给定一个矩形,必然存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍.猜想,证明与拓广老师提示:
在探索结论:“任意给定一个矩形,必然存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍.”的过程中,我们经历了猜想,由特殊到一般的尝试,证明,拓广的全过程,从而得到了一般性的结论.任意给定一个矩形,是否一定存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半?
你准备怎么去做?猜想,证明与拓广挑战“自我”小明认为,这个结论是正确的,理由是:既然任意给定一个矩形,必然存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍.也就是任何一个矩形 的周长和面积可以同时“加倍”,那么,原矩形自然满足新矩形的“减半”要求,即原矩形的周长和面积分别是新矩形周长和面积的一半.猜想,证明与拓广小明认为,这个结论是正确的,理由是:既然任意给定一个矩形,必然存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍.也就是任何一个矩形的周长和面积可以同时“加倍”,那么,原矩形自然满足新矩形的“减半”要求,即原矩形的周长和面积分别是新矩形周长和面积的一半. 挑战“自我”如果矩形的长和宽分别仍为2和1,那么是否存在一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半?
如果已知矩形的长和宽分别为3和1,是否还有相同的结论?
如果已知矩形的长和宽分别为4和1,5和1,……,n和1呢?挑战“自我”由特殊到一般解:如果矩形的长和宽分别为2和1,那么其周长和面积分别为6和2,所求矩形的周长和面积应分别为3和1.设所求矩形的长为x,那么它宽为1.5-x,其面积为x(1.5-x).根据题意,得
x(1.5-x)=1.
即 2x2-3x+2=0.
如果这个方程有解,则说明这样的矩形存在.
由b2-4ac=32-4×2×2=-7<0,知道这个方程没有实数根.挑战“自我”由特殊到一般结论:如果矩形的长和宽分别为2和1,那么不存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半.解:当如果矩形的长和宽分别为3和1,4和1,5和1时.设所求矩形的长为x, 根据题意所得的方程均有没有实数根解,则说明这样的矩形不存在.挑战“自我”结论:如果矩形的长和宽分别为2和1,3和1,4和1,5和1时.都不存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半.由特殊到一般挑战“自我”由特殊到一般我们已经知道:如果矩形的长和宽分别为2和1,3和1,4和1,5和1时.都不存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半.这个结论是否具有一般性?
如果这个结论不具有一般性,那么当矩形的长和宽满足什么条件时,才存在一个新的矩形,它的周长和面积分别是已知矩形的周长和面积的一半?你能再找出这样的一个例子吗?挑战“自我”由特殊到一般解:如果矩形的长和宽分别为6和1,那么其周长和面积分别为14和6,所求矩形的周长和面积应分别为7和3.设所求矩形的长为x,那么它宽为3.5-x,其面积为x(3.5-x).根据题意,得
x(3.5-x)=3.
即 2x2-7x+6=0.
由b2-4ac=72-4×2×6=1>0,知道这个方程有实数根:结论:如果矩形的长和宽分别为6和1时.存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半.挑战“自我”由特殊到一般解:如果矩形的长和宽分别为m和n,那么其周长和面积分别为2(m+n)和mn,所求矩形的周长和面积应分别为m+n和mn/2.设所求矩形的长为x,那么它宽为(m+n)/2-x,其面积为x[(m+n)/2-x].根据题意,得
x[(m+n)/2-x]=mn/2.
即 2x2-(m+n)x+mn=0.
由Δ=b2-4ac=(m+n)2-4×2×mn=m2+n2-6mn.
知道只有当m2+n2≥6mn时,这个方程才有实数根:结论:如果矩形的长和宽满足m2+n2≥6mn时.才存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半.挑战“自我”神奇的反比例函数同学们,我们已经知道用反比例函数可以解答世界数学难题:化圆为方,倍立方体.今天我们再来《读一读》P155反比例函数的又一个杰作.换一个角度看数学真奇妙知识的升华P155习题 1~4题.
祝你成功！结束寄语函数来自现实生活,函数是描述现实世界变化规律的重要数学模型.
函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要手段.
从函数的图象中获取信息的能力是学好数学必需具有的基本素质.