24.1.2 垂直于弦的直径说课课件
文档属性
| 名称 | 24.1.2 垂直于弦的直径说课课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-19 00:00:00 | ||
图片预览



文档简介
课件23张PPT。《垂直于弦的直径》人教版初中数学九年级上册第二十四章教材
分析教学重
难点分
析
教法学
法分析教学
流程说
课
流
程教学
策略1、地位和作用:
既是前面圆的性质的重要体现,是圆的轴对称性的具体化,也是今后证明线段相等、角相等、弧相等、垂直关系的重要依据,同时也是为进行圆的计算和作图提供了方法和依据.
本节知识在中招考试中所占的分值:一、教材分析2、教学目标
(1)知识技能:
①使学生理解圆的轴对称性;
②掌握垂径定理;
③学会运用垂径定理解决有关的证明、计算和作图问题。
(2)能力目标:
培养学生观察能力、分析能力及联想能力。
(3)情感目标:
通过联系、发展、对立与统一的思考方法对学生进行辩证唯物主义观点及美育教育.
(4)数学思考:
经历将已学知识应用到未学知识的探索过程,发展学生的数学思维。 重点:垂径定理及其应用。难点:对垂径定理题设与结论的区分及
定理的证明方法.
关键:理解垂径定理的关键是圆的轴对
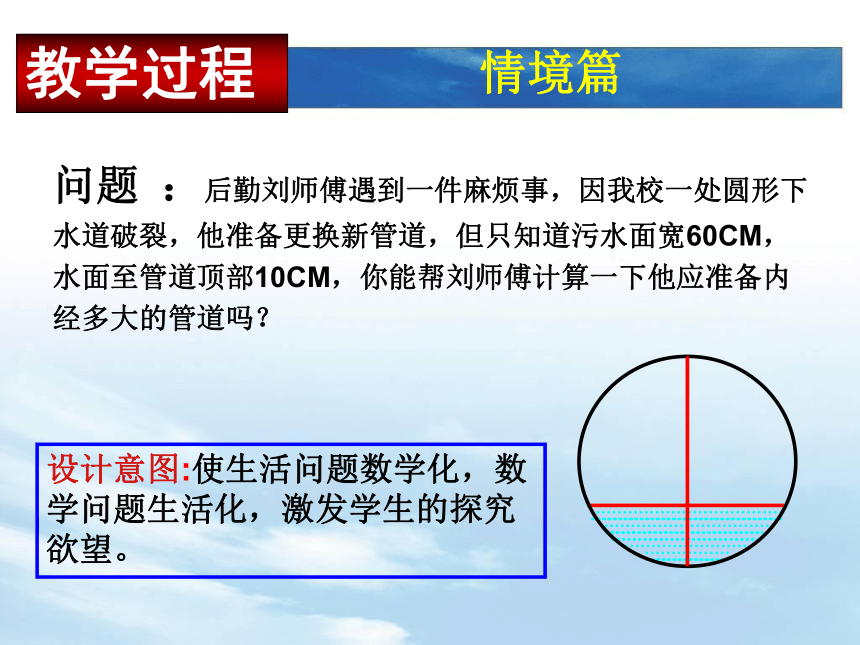
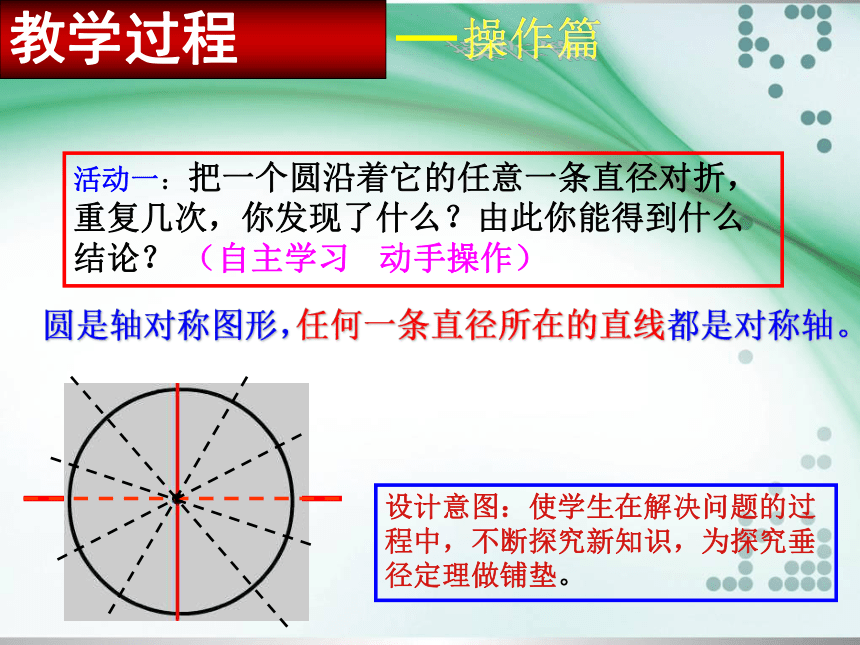
称性.二、重难点分析三交流一反馈参与式探究教学法三、教法学法分析 情景篇(2分钟)四、教学过程问题 :后勤刘师傅遇到一件麻烦事,因我校一处圆形下水道破裂,他准备更换新管道,但只知道污水面宽60CM,水面至管道顶部10CM,你能帮刘师傅计算一下他应准备内经多大的管道吗?设计意图:使生活问题数学化,数学问题生活化,激发学生的探究欲望。情境篇教学过程活动一:把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论? (自主学习 动手操作)操作篇圆是轴对称图形,任何一条直径所在的直线都是对称轴。设计意图:使学生在解决问题的过程中,不断探究新知识,为探究垂径定理做铺垫。教学过程(板块一)自学指导:
内容:课本P80----P81
要求:思考以下问题:
1、什么是垂径定理?你能用几何语言
描述出来吗?
2、你是用什么方法证明的?
方法:观察—归纳
时间:8分钟后班级交流验证篇 处理方法:根据教师的自学指导,学生边看书边用红笔圈画出重点、难点、疑点。教学过程(板块二)验证篇小组交流:
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为E ,你能找出图中相等的量吗?你通过什么样的方式得到结论?
·OABCDE设计意图:
通过小组合作交流,教师演示,得出叠合法的证明方法,突破本节课的一个难点。教学过程垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.·OABCDE验证篇:(板块三)设计意图:使学生充分参与探索,感受数学学习的过程,注重知识的生成过程,体会数形结合的思想。教学过程一、例题:如图所示,在⊙O中,OC⊥AB于C,
OA=2cm,OC=1cm,求弦AB的长。应用篇教学过程解题方法总结:
1、见半弦、半径、弦心距三者构造直角
三角形来解决;
2、常用辅助线:过圆心 做垂直。
变式练习:(学生演板)
变式 1 在⊙O中,弦AB的长为8,圆心O到AB的距离为3,求⊙O 的半径。
变式2 AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,CD=1, 求弦AB的长。
变式3 ⊙O的半径为5,弦AB的长为6,则AB的弦心距长为 .
应用篇教学过程设计意图:通过定理的变式,使学生能灵活运用垂径定理解决圆的有关计算问题。总结篇学习笔记展示教学过程总结篇学习笔记展示总结篇学习笔记展示总结篇学习笔记展示板书设计总结篇反馈检测
必做题:
1、如图,圆弧形桥拱的跨度AB=12米,
拱高CD=4米,求拱桥的半径。
2、如图, 圆弧形蔬菜大棚的剖面如
图所示AB=8m,∠CAD=30°,求大棚高度CD。
3、如图,在⊙O中,AB、AC是互相垂
直的两条弦,OD⊥AB于D,OE⊥AC于E,
且AB=8cm,AC=6cm,那 么⊙O的半径
OA长为____________.
选做题:
1、如图所示,⊙O中,弦CD交直径AB
于点P,AB=12cm,PA:PB=1:5,
且∠BPD=30°,求CD的长。升华篇设计意图:对不同学生采取分类要求、分层达标!注重一个“效”字
灵活运用一个“变”字
贯穿一个“做”字
凸显一个“能”字
体现一个“乐”字
五、教学策略当学生茫无头绪时,
我能给他以启迪; 当学生没有信心时,
我能唤起他们的力量; 我竭尽全能使学生的思维擦出火花; 我愿学生在课堂上学习合作,感受和谐的欢乐;
我愿学生在课堂上“豁然开朗”、“茅塞顿开” …理想课堂欢迎各位
批评指导!
分析教学重
难点分
析
教法学
法分析教学
流程说
课
流
程教学
策略1、地位和作用:
既是前面圆的性质的重要体现,是圆的轴对称性的具体化,也是今后证明线段相等、角相等、弧相等、垂直关系的重要依据,同时也是为进行圆的计算和作图提供了方法和依据.
本节知识在中招考试中所占的分值:一、教材分析2、教学目标
(1)知识技能:
①使学生理解圆的轴对称性;
②掌握垂径定理;
③学会运用垂径定理解决有关的证明、计算和作图问题。
(2)能力目标:
培养学生观察能力、分析能力及联想能力。
(3)情感目标:
通过联系、发展、对立与统一的思考方法对学生进行辩证唯物主义观点及美育教育.
(4)数学思考:
经历将已学知识应用到未学知识的探索过程,发展学生的数学思维。 重点:垂径定理及其应用。难点:对垂径定理题设与结论的区分及
定理的证明方法.
关键:理解垂径定理的关键是圆的轴对
称性.二、重难点分析三交流一反馈参与式探究教学法三、教法学法分析 情景篇(2分钟)四、教学过程问题 :后勤刘师傅遇到一件麻烦事,因我校一处圆形下水道破裂,他准备更换新管道,但只知道污水面宽60CM,水面至管道顶部10CM,你能帮刘师傅计算一下他应准备内经多大的管道吗?设计意图:使生活问题数学化,数学问题生活化,激发学生的探究欲望。情境篇教学过程活动一:把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论? (自主学习 动手操作)操作篇圆是轴对称图形,任何一条直径所在的直线都是对称轴。设计意图:使学生在解决问题的过程中,不断探究新知识,为探究垂径定理做铺垫。教学过程(板块一)自学指导:
内容:课本P80----P81
要求:思考以下问题:
1、什么是垂径定理?你能用几何语言
描述出来吗?
2、你是用什么方法证明的?
方法:观察—归纳
时间:8分钟后班级交流验证篇 处理方法:根据教师的自学指导,学生边看书边用红笔圈画出重点、难点、疑点。教学过程(板块二)验证篇小组交流:
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为E ,你能找出图中相等的量吗?你通过什么样的方式得到结论?
·OABCDE设计意图:
通过小组合作交流,教师演示,得出叠合法的证明方法,突破本节课的一个难点。教学过程垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.·OABCDE验证篇:(板块三)设计意图:使学生充分参与探索,感受数学学习的过程,注重知识的生成过程,体会数形结合的思想。教学过程一、例题:如图所示,在⊙O中,OC⊥AB于C,
OA=2cm,OC=1cm,求弦AB的长。应用篇教学过程解题方法总结:
1、见半弦、半径、弦心距三者构造直角
三角形来解决;
2、常用辅助线:过圆心 做垂直。
变式练习:(学生演板)
变式 1 在⊙O中,弦AB的长为8,圆心O到AB的距离为3,求⊙O 的半径。
变式2 AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,CD=1, 求弦AB的长。
变式3 ⊙O的半径为5,弦AB的长为6,则AB的弦心距长为 .
应用篇教学过程设计意图:通过定理的变式,使学生能灵活运用垂径定理解决圆的有关计算问题。总结篇学习笔记展示教学过程总结篇学习笔记展示总结篇学习笔记展示总结篇学习笔记展示板书设计总结篇反馈检测
必做题:
1、如图,圆弧形桥拱的跨度AB=12米,
拱高CD=4米,求拱桥的半径。
2、如图, 圆弧形蔬菜大棚的剖面如
图所示AB=8m,∠CAD=30°,求大棚高度CD。
3、如图,在⊙O中,AB、AC是互相垂
直的两条弦,OD⊥AB于D,OE⊥AC于E,
且AB=8cm,AC=6cm,那 么⊙O的半径
OA长为____________.
选做题:
1、如图所示,⊙O中,弦CD交直径AB
于点P,AB=12cm,PA:PB=1:5,
且∠BPD=30°,求CD的长。升华篇设计意图:对不同学生采取分类要求、分层达标!注重一个“效”字
灵活运用一个“变”字
贯穿一个“做”字
凸显一个“能”字
体现一个“乐”字
五、教学策略当学生茫无头绪时,
我能给他以启迪; 当学生没有信心时,
我能唤起他们的力量; 我竭尽全能使学生的思维擦出火花; 我愿学生在课堂上学习合作,感受和谐的欢乐;
我愿学生在课堂上“豁然开朗”、“茅塞顿开” …理想课堂欢迎各位
批评指导!
同课章节目录
